在學習線性迴歸的時候很多課程都會講到用梯度下降法求解引數，對於梯度下降演算法怎麼求出這個解講的較少，自己實現一遍演算法比較有助於理解演算法，也能注意到比較細節的東西。具體的數學推導可以參照這一篇部落格（http://www.cnblogs.com/pinard/p/5970503.html）

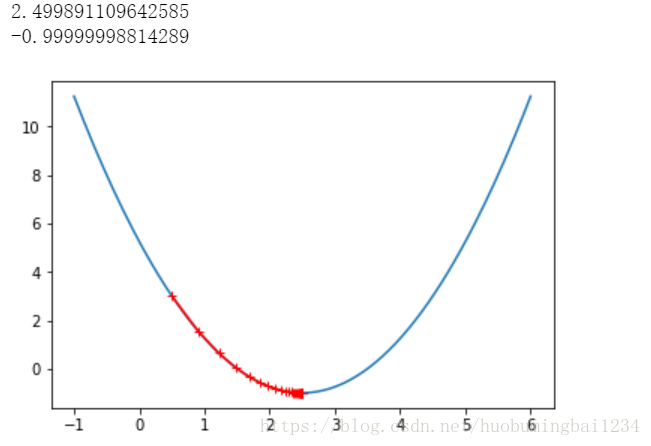
一、       首先，我們用一個簡單的二元函式用梯度下降法看下演算法收斂的過程

              也可以改一下eta，看一下步長如果大一點，演算法的收斂過程

import numpy as np
import matplotlib.pyplot as plt

plot_x = np.linspace(-1,6,140)
plot_y = (plot_x-2.5)**2-1

#先算出來當前函式的導數
def dJ(theta):
    return 2*(theta-2.5)

#梯度函式
def J(theta):
    return (theta-2.5)**2-1


#初始化theta=0
#步長eta設定為0.1
eta = 0.1
theta_history = []
theta = 0
epsilon = 1e-8
while True:
    gredient = dJ(theta)
    last_theta = theta
    theta = theta - eta*gredient
    theta_history.append(theta)
    
    if(abs(J(theta) - J(last_theta)) < epsilon):
        break
        
print(theta)
print(J(theta))

plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history),J(np.array(theta_history)),color='r',marker='+')
plt.show()
 

出來的結果如下：

二、線上性迴歸模型中訓練演算法--批量梯度下降Batch Gradient Descent

首先，構建一個函式

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = 2 * np.random.random(size=100)
y = x*3. + 4. + np.random.normal(size=100)


#然後改成向量的形式
X = x.reshape(-1,1)

plt.scatter(x,y)
plt.show()

然後寫實現梯度下降法求解我們構建的這個函式：

def J(theta , X_b , y):
    try:
        return sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')



#這裡使用的是每次求一個引數，然後組合在了一起成了res
def dJ(theta, X_b ,y):
    res = np.empty(len(theta))
    res[0] = np.sum(X_b.dot(theta) - y)
    for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
    return res * 2 / len(X_b)


#這裡也可以直接用矩陣運算求出所有的引數，效率更高
#return X_b.T.dot(X_b.dot(theta)-y)*2. / len(y)





 

然後把上面的過程封裝成函式形式：

#把整個演算法寫成函式的形式

def gradient_descent(X_b, y ,inital_theta, eta ,n_inters = 1e4, epsilon = 1e-8):
    theta = initial_theta
    i_inter = 0
    
    while i_inter < n_inters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta*gradient
    
        if(abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < epsilon):
            break
        
        i_inter += 1
    return theta

然後用我們實現的演算法求解上面那個函式：

#這裡加一列1
X_b = np.hstack([np.ones((len(x),1)), x.reshape(-1,1)])
#初始theta設定為0
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)
theta

輸出結果如下：

array([4.02145786, 3.00706277])

使用梯度下降法時，由於不同維度之間的值大小不一，最好將資料進行歸一化，否則容易造成不收斂

三、線上性迴歸模型中訓練演算法--隨機梯度下降Stochastic Gradient Descent

   隨機梯度下降法可以訓練更少的樣本就得到比較好的效果，下面用兩段程式碼比較下。

這個就是之前的批量梯度下降，不過換了一個數據集

import numpy as np
import matplotlib.pyplot as plt

m = 100000

x = np.random.normal(size = m)
X = x.reshape(-1,1)
y = 4. * x + 3. +np.random.normal(0,3,size = m)

def J(theta , X_b , y):
    try:
        return sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')
    
def dJ(theta, X_b ,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2. / len(y) 


def gradient_descent(X_b, y ,inital_theta, eta ,n_inters = 1e4, epsilon = 1e-8):
    theta = initial_theta
    i_inter = 0
    
    while i_inter < n_inters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta*gradient
    
        if(abs(J(theta,X_b,y) - J(last_theta,X_b,y)) < epsilon):
            break
        
        i_inter += 1
    return theta

%%time
X_b = np.hstack([np.ones((len(x),1)), X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)
theta

結果如下：

Wall time: 37.2 s

theta：

array([3.00590902, 4.00776602])

下面我們用隨機梯度下降：

#這裡每次求一行資料的梯度,所以後面不用除以m
def dJ_sgd(theta, X_b_i, y_i):
    return X_b_i.T.dot(X_b_i.dot(theta) - y_i)* 2. 


#隨機梯度下降法學習率設定t0/(t+t1)這種形式
#由於梯度下降法隨機性，設定最後的結果的時候只設置最大迭代次數
def sgd(X_b, y, initial_theta, n_iters):
    
    t0 = 5
    t1 = 50
    
    def learning_rate(t):
        return t0/(t+t1)
    
    theta = initial_theta
    for cur_iter in range(n_iters):
        #下面是設定每次隨機取一個樣本
        rand_i = np.random.randint(len(X_b))
        gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
        theta = theta - learning_rate(cur_iter) * gradient
        
    return theta


%%time
X_b = np.hstack([np.ones((len(x),1)), X])
initial_theta = np.zeros(X_b.shape[1])

theta = sgd(X_b, y, initial_theta, n_iters=len(X_b)//3)

結果如下：

Wall time: 481 ms

theta:

array([2.93906903, 3.99764075])

對比下兩者的執行時間，隨機梯度下降法計算量更小，時間也大大減少。

四、小批量梯度下降法-Mini-Batch Gradient Descent

這個完全按照自己理解寫下，如果有大牛指點下不勝感激。

小批量梯度下降法主要在於每次訓練的資料量不同，隨機梯度下降是有一個樣本就訓練一次，小批量梯度下降是有一批樣本訓練一次，這裡預設引數我給100

#這裡每次求一行資料的梯度,所以後面不用除以m
def dJ_sgd(theta, X_b_i, y_i):
    return X_b_i.T.dot(X_b_i.dot(theta) - y_i)* 2. 


def sgd(X_b, y, initial_theta, n_iters,n=100):
    
    t0 = 5
    t1 = 50
    
    def learning_rate(t):
        return t0/(t+t1)
    
    theta = initial_theta
    for cur_iter in range(n_iters):
        #下面是設定每次隨機取一個樣本
        for i in range(n):
            rand_i = []
            rand_i_1 = np.random.randint(len(X_b))
            rand_i.append(rand_i_1)
            
        gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
        theta = theta - learning_rate(cur_iter) * gradient
    return theta

然後還是用之前的資料集測試下：

%%time
import numpy as np
X_b = np.hstack([np.ones((len(x),1)), X])
initial_theta = np.zeros(X_b.shape[1])

theta = sgd(X_b, y, initial_theta,n=5, n_iters=len(X_b)//3)

結果如下：

Wall time: 643 ms

這裡每次給5個樣本，耗費的時間還是很長的，不知道是不是程式碼寫的有問題。

結果來看是對的:

array([2.96785569, 4.00405719])