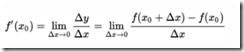導數,偏導,方向倒數,梯度
阿新 • • 發佈:2019-01-24
知乎連結
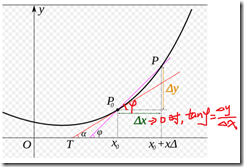
導數:
導數不僅僅表示該點切線的斜率,還反應了函式在該點的變化率。
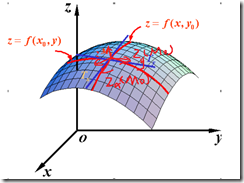
偏導數:
偏導數僅僅是表示某點在x方向的導數和再y軸方向的導數。
這反應了偏導數的侷限性,僅僅是多元函式沿著座標軸的變化率,但是如上圖,在M0點處存在很多方向的偏導數(並不僅僅x和y方向)。這就引出了方向導數。
方向導數:
我們不僅僅要知道函式在座標軸方向上的變化率(即偏導數)還需要設法求得函式在其他方向上的變化率。而方向導數就是函式在其他特定方向上的變化率。
方向導數的定義和導數定義類似,只不過是在多個維度上。例如在三維空間中:
設三元函式f在點P0(x0,y0,z0)的某鄰域內有定義,l為從點P0出發的射線,P(x,y,z)為l上且含於 鄰域內的任一點,以ρ(rou)表示P和P0兩點間的距離。若極限
lim( (f(P)-f(P0)) / ρ )= lim (△l f / ρ)(當ρ→0時)
存在,則稱此極限為函式f在點P0沿方向l的方向導數
梯度:
由上面的方向導數可知,方向導數是在各個方向上都有,而且每個方向上的變化一般是不一樣的,那到底沿哪個方向最大呢?沿哪個方向最小呢?為了研究方便,就有了梯度的定義。
下圖是梯度的定義:
梯度是眾多方向導數中最大的那個向量,這個方向就用梯度來表示(grad=ai+bj)這個向量來表示,其中a是函式在x方向上的偏導數,b是函式在y方向上的偏導數,梯度的模就是這個最大方向導數的值。