【Foundation of data science】Clustering
阿新 • • 發佈:2019-04-23
監督學習 由於 clas mea ado 概率 我們 給定 放置 document.title="【Foundation of data science】Clustering"
Clustering ,翻譯為"聚類",就是把相似的東西分為一組,同 Classification(分類)不同, classifier 從訓練集中進行"學習",從而能夠對未知數據進行分類,這種提供訓練數據的過程叫做 supervised learning (監督學習),而在聚類的時候,我們並不關心某一類是什麽,我們只需要把相似的東西聚到一起,因此,一個聚類算法通常只需要知道如何計算相似度就可以工作了,因此 clustering 通常並不需要使用訓練數據進行學習,這在 Machine Learning 中被稱作 unsupervised learning (無監督學習)。 ## 一、聚類的兩種常用的假設
$$
\Phi_{k c e n t e r}(\mathcal{C})=\max _{j=1} \max _{\mathbf{a}_{i} \in C_{j}} d\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
例如,消防站位置問題(最小化消防站可能需要前往的最大距離)。
2. **k-median clustering:** 最小化數據點到其中心的距離之和,即minimize$$
$$
k-median比k-center更具有抗噪性,因為少數異常值通常不會更改最佳解決方案。
3. **k-means clustering:** 最小化數據點到其中心的距離平方和,即mminimize$$
\Phi_{k m e a n s}(\mathcal{C})=\sum_{j=1}^{k} \sum_{\mathbf{a}_{i} \in C_{j}} d^{2}\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
k-means比k-median更重視異常值,因為對距離進行了平方,這會放大大的值。 當數據由$R^d$中的點組成時,更常使用k-means準則,而當我們具有有限度量時,k-median更常用,即數據是具有邊距離的圖中的節點。
### 2、高密度聚類
如果我們不相信我們的聚類是基於中心的,那麽通常做出的的另一個假設是聚類由高密度區域組成,他們之間是低密度的“護城河”。
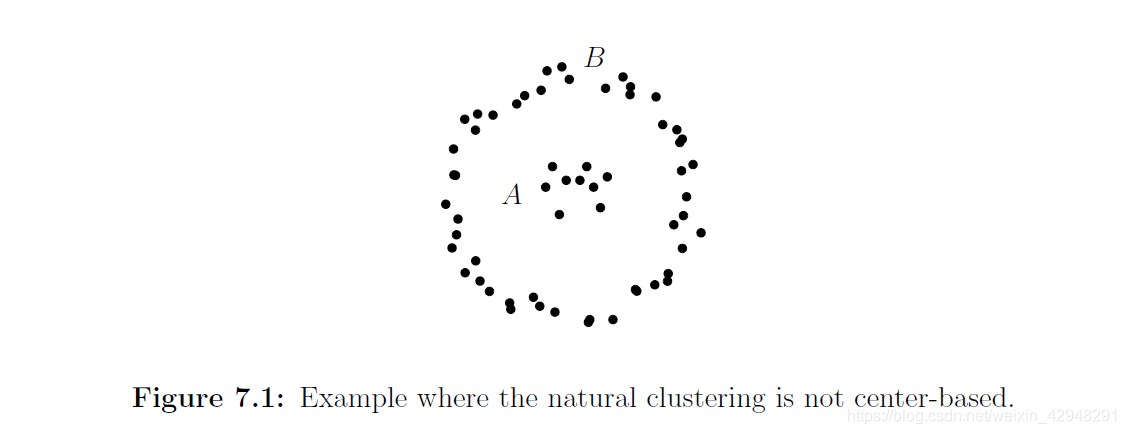
## 二、k-Means Clustering
### 1、動機
考慮使用k-means準則的最大似然動機。假設我們的數據是由k個良好分離的球形高斯密度等權混合生成的,這k個高斯密度的均值分別為$\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$,方差都為1。從而混合分布的密度為$$
\operatorname{Prob}(\mathrm{x})=\frac{1}{(2 \pi)^{d / 2}} \frac{1}{k} \sum_{i=1}^{k} e^{-\left|\mathrm{x}-\mu_{i}\right|^{2}}
$$
定義最接近x的中心為$\mu(x)$,由於指數函數快速下降,我們可以用$e^{-|\mathbf{x}-\boldsymbol{\mu}(\mathbf{x})|^{2}}$近似$\sum_{i=1}^{k} e^{-\left|\mathbf{x}-\boldsymbol{\mu}_{i}\right|^{2}}$。因此,$$
\operatorname{Prob}(\mathbf{x}) \approx \frac{1}{(2 \pi)^{d / 2} k} e^{-|\mathbf{x}-\mu(\mathbf{x})|^{2}}
$$
從而,從混合分布中選擇樣本點的可能性為$$
\frac{1}{k^{n}} \frac{1}{(2 \pi)^{n d / 2}} \prod_{i=1}^{n} e^{-\left|\mathbf{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}=c e^{-\sum_{i=1}^{n}\left|\mathrm{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}
$$
因此,最小化到聚類中心的距離平方和得到最大似然 $\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$。
### 2、k-means目標的性質
**引理2.1** 當x是質心時,數據點到x的距離平方和得到最小化,即$\mathbf{x}=\frac{1}{n} \sum_{i} \mathbf{a}_{\mathbf{i}}$。
**證明**:我們的目標是尋找x,最小化$\sum_{i}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{x}\right|^{2}$。通過簡單計算可得
$$
\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{x}\right|^{2}=\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{c}\right|^{2}+n|\mathrm{c}-\mathrm{x}|^{2}
$$等式右邊第一部分是確定的數,第二部分最小值為0,在$x=c$處取得。
### 3、Lloyd‘s Algorithm
k-means聚類一個常用的算法是Lloyd‘s Algorithm。
**Lloyd‘s Algorithm:**
1. 初始化k個中心(隨機選擇?);
2. 將每個點與最靠近它的中心聚類;
3. 找到每個聚類的質心作為新中心替換舊中心;
4. 重復Step 2和Step 3直到聚類中心收斂(根據一些準則,例如k-means得分不再提高) Lloyd算法不一定能找到全局最優解,但會找到局部最優解。算法中一個重要的步驟是初始化。下面的例子說明了初始中心會顯著影響聚類結果。
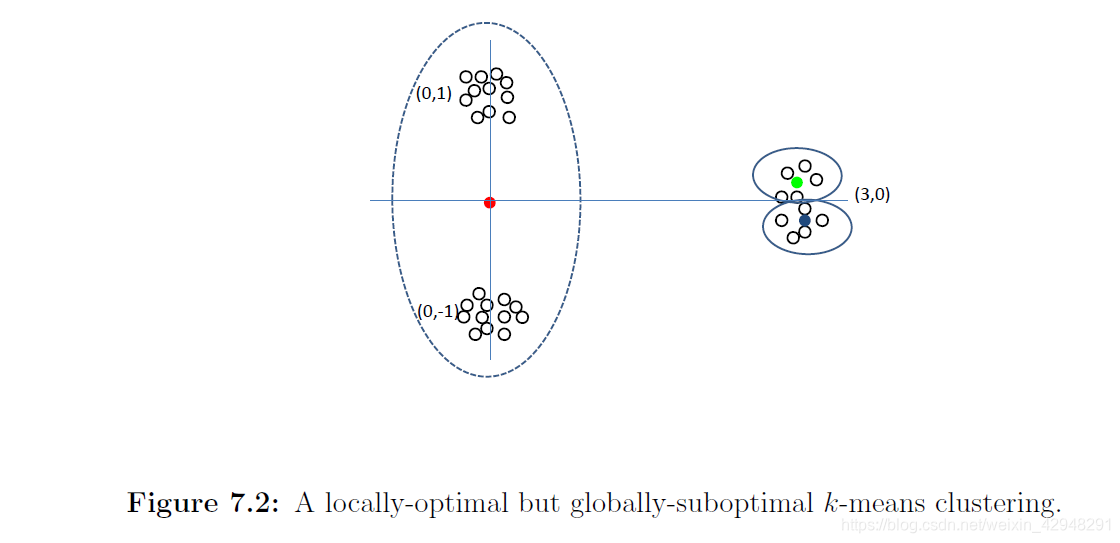
上圖中有三個密集簇,分別以$(0,1),(0,-1)$和$(3,0)$為中心。但如果我們以一個中心$(0,1)$和兩個接近$(3,0)$的中心初始化,那麽$(0,1)$處的中心會移到$(0,0)$,而$(3,0)$處的兩個中心會呆在那裏,將這一簇分成兩部分。 因此,對於初始中心的選擇要遵循一定的策略。最常用的策略為“最遠遍歷”。首先選擇一個數據點作為初始中心$c_1$,然後選擇距離$c_1$最遠的數據點作為$c_2$,然後選擇距離$\{c_1,c_2\}$最遠的數據點作為$c_3$,等等。直到選足了k個點,將它們用作初始中心。註意到,這樣可以在圖7.2中得到正確的聚類。 “最遠便利”會被少數異常值欺騙。k-means++對此進行改進,基於它們與已挑選中心的距離來加權數據點,具體而言,與距離平方成比例。然後根據這些權重概率地選擇下一個中心。另一種方法是為k-means問題運行一些其他近似算法,然後使用其輸出作為Lloyd算法的起點。 ### 4、Ward‘s Algorithm
從它自己的簇中的每個數據點開始,然後重復的合並成對的簇,直到只剩下k個簇。具體來說,Ward算法合並了最小化k-means成本增量的兩個簇,即合並 $\left(C, C^{\prime}\right)$ minimizing
$$
\operatorname{cost}\left(C \cup C^{\prime}\right)-\operatorname{cost}(C)-\operatorname{cost}\left(C^{\prime}\right)
$$
### 4、一維中的k-Means聚類
假設已經得到了$a_{1}, \dots, a_{i}$的所有最優k‘-means聚類($\forall k‘\le k$), 要計算$a_{1}, \dots, a_{i+1}$的最優k‘-means聚類,即尋找$j$,最小化
$$dist(a_1,\cdots,a_{j-1})+dist(a_j,\cdots,a_{i+1})$$
前者聚成$k‘-1$類,後者聚成1類。 對於給定的$i$,我們需要計算$k‘=1,\cdots,k$,每次計算$a_{1}, \dots, a_{i}$的k‘-means聚類時,需要運行$i$個$j$($i\le n$)。因此運行時間為$O(kn)$。而一共有$n$個$i$,因此總的運行時間為$O(kn^2$)。 ## 三、k-Center Clustering
將任意點到聚類中心的最大距離稱為聚類的半徑。存在半徑為r的k聚類當且僅當存在k個半徑為r的球體將所有的點覆蓋。下面,我們給出一個簡單的算法來尋找k個球覆蓋所有點。
**The Farthest Traversal k-clustering Algorithm** 1. 任意選擇一個點作為第一個聚類中心;
2. 對$t=2,3,\cdots,k$,選擇距離當前聚類中心最遠的點,作為第$t$個聚類中心。 該算法相當於初始化Lloyd算法的最遠遍歷策略。下面的引理表明該算法僅需要使用最多為最佳k-center解的兩倍的半徑。
**Theorem 7.3** 如果存在半徑為$\frac{r}{2}$的$k$聚類,那麽上面的算法找到的$k$聚類的半徑至多為$r$。
**證明**:若不然,即存在數據點$x$,它距離所有中心$>r$ $\Rightarrow$ 每次產生的新中心距離當前中心$>r$ (否則它就不是距離當前中心最遠的點,因為$x$距離當前中心$>r$ )。從而,$k$個中心加上一個數據點$x$,共有$k+1$個數據點,它們的距離成對的比$r$更大。但在半徑為$\frac{r}{2}$的$k$聚類中,沒有兩個這樣的點可以屬於同一簇,矛盾。
## 四、Spectral Clustering(譜聚類)
Spectral Clustering 其實就是通過 Laplacian Eigenmap 的降維方式降維之後再做 K-means 的一個過程。
譜聚類遵循以下步驟: - 尋找由A的前k個右奇異向量生成的空間V
- 將數據點投影到V上
- 對投影點聚類
### 1、為什麽要投影?
投影會使數據點更接近其聚類中心。
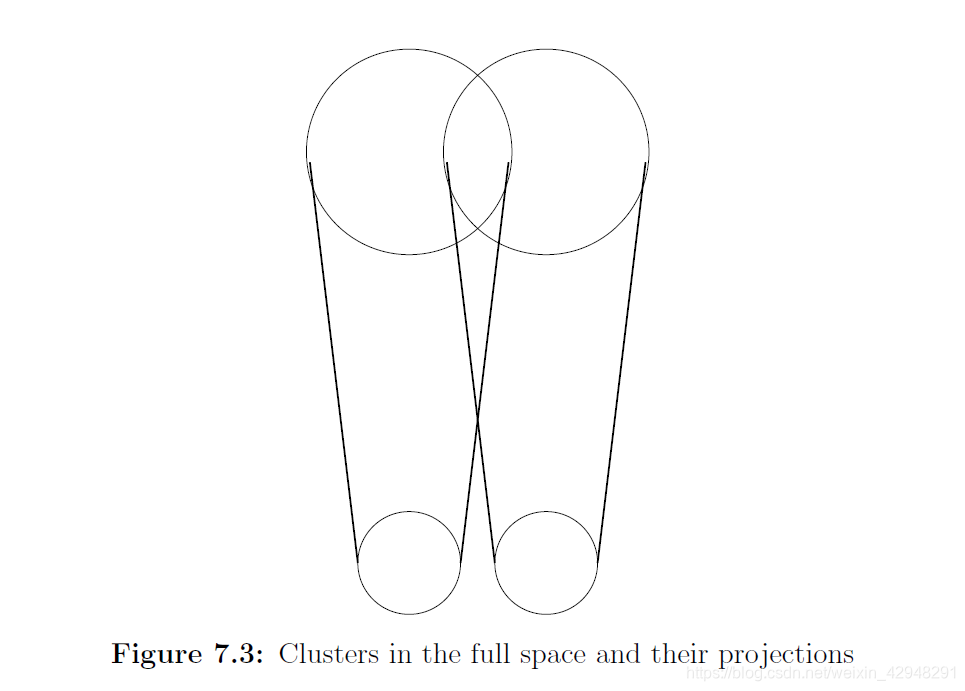
令數據矩陣$A$的第$i$行表示第$i$個數據點,C的第$i$行表示第$i$個數據點屬於的中心點。(對於$k$聚類問題有且僅有$k$個不同行)那麽,數據點到其聚類中心的距離平方和為
$$
\sum_{i=1}^{n}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{c _ { i }}\right|^{2}=\|A-C\|_{F}^{2}
$$
通過聚類能夠將到聚類中心的距離平方和由$\|A-C\|_{F}^{2}$減小到投影中的8$k\|A-C\|_{2}^{2}$.。
**Theorem 7.4** 對任意秩小於等於k的矩陣$C$,有
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k\|A-C\|_{2}^{2}
$$
**證明**:$$rank(A_k-C)\le rank(A_k) + rank(C)\le k+k=2k$$
由於$\|A\|_{2}^{2} \leq\|A\|_{F}^{2} \leq k\|A\|_{2}^{2}$,所以
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 2 k\left\|A_{k}-C\right\|_{2}^{2}
$$
又
$$
\left\|A_{k}-C\right\|_{2} \leq\left\|A_{k}-A\right\|_{2}+\|A-C\|_{2} \leq 2\|A-C\|_{2}
$$
得證。
### 2、算法
定義$\sigma(C)=\|A-C\|_{2} / \sqrt{n}$。
**Spectral Clustering - The Algorithm**
- 尋找A的前k個奇異值向量,然後將A的列投影到由這向量生成的空間上,得到$A_k$;
- 從$A_k$中選擇一行進行聚類,使得$A_k$的所有行與該行的距離都小於$6k \sigma(C) / \varepsilon$;
- 重復Step 2 $k$次。 **Theorem 7.5** 如果在$k$聚類$C$中,每對中心間隔至少15$k \sigma(C) / \varepsilon$,並且每一類中至少有$\varepsilon n$個點,則以至少$1-\varepsilon$的概率,譜聚類找到的聚類$C‘$與$C$至多有$\varepsilon^{2} n$個點不同。
**證明**:首先證明對大多數的數據點,數據點的投影與其聚類中心的距離在$3k \sigma(C) / \varepsilon$以內。令
$$
M=\left\{i :\left|\mathbf{v}_{\mathrm{i}}-\mathbf{c}_{\mathrm{i}}\right| \geq 3 k \sigma(C) / \varepsilon\right\}
$$
其中$\mathbf{v}_i$表示$A_k$的第$i$行。下面證明$|M|$是小的。
由於$\left\|A_{k}-C\right\|_{F}^{2}=\sum_{i}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq \sum_{i \in M}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}}$,所以,由定理7.4,有
$$
|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}} \leq\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k n \sigma^{2}(C) \quad \Longrightarrow \quad|M| \leq \frac{8 \varepsilon^{2} n}{9 k}
$$
如果$i \notin M$,稱數據點$i$是好的。對於屬於同一簇的兩個好點$i$和$j$,由於它們的投影與中心距離在$3k \sigma(C) / \varepsilon$以內,所以兩個點的投影距離在$6k \sigma(C) / \varepsilon$以內。另一方面,對於屬於不同簇的兩個好點$i$和$k$,由於兩個簇的中心間隔至少15$k \sigma(C) / \varepsilon$,所以兩個點的投影距離一定比$15 k \sigma(C) / \varepsilon-6 k \sigma(C) / \varepsilon=9 k \sigma(C) / \varepsilon$大。因此,如果我們在Step 2中選擇了一個好點(如點$i$),那麽我們算法放置在它的簇中的好點就確為與$i$在同一簇中的好點。因此,如果在Step 2的第k次執行中,我們選擇了一個好點,那麽所有好點都被正確聚類。又由於$|M| \leq \varepsilon^{2} n$,定理即成立。
為了完成證明,,我們還需說明Step 2中選擇壞點的可能性很小。有上面證明,可知每一類中好點的個數至少$(\varepsilon-\varepsilon^2)n$。因此,從每一類中挑出好點的概率至少為$(\varepsilon-\varepsilon^2)n/(\varepsilon n)=1-\varepsilon$。
### 3、由$\Omega(1)$標準差分離的均值
對於實線上的概率分布,“由$6$標準差分離的均值”足夠區分不同的分布。如果$k \in O(1)$並且$6$被一些常數代替,則譜聚類能夠使我們在更高維度上做同樣的事。首先定義標準偏差為數據點到聚類中心的平方均值在所有單位方向$\mathrm{v}$上的最大值,即
$$
\sigma(C)^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1} \sum_{i=1}^{n}\left[\left(\mathbf{a}_{\mathbf{i}}-\mathbf{c}_{\mathbf{i}}\right) \cdot \mathbf{v}\right]^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1}|(A-C) \mathbf{v}|^{2}=\frac{1}{n}\|A-C\|_{2}^{2}
$$
這也與我們之前對$\sigma(C)$的定義相同。
現在,很容易看出Theorem 7.5可以重新表述(假設$k \in O(1)$)為 - 如果$C$中的聚類中心可以由$\Omega(\sigma(C))$分離,那麽譜聚類算法找到的聚類$C‘$與$C$只有很小一部分數據點不同。 可以看出,對於許多隨機模型,“均值由$\Omega(1)$標準差分離”條件成立。在這裏用兩個例子說明。 首先,假設我們有$k \in O(1)$個球面高斯的混合,其標準差均為1。數據由這個混合產生。如果高斯的均值是$\Omega(1)$分離的,那麽條件“均值由$\Omega(1)$標準差分離”是滿足的,因此當我們投影到SVD子空間並聚類,我們將得到(接近)正確的聚類。 我們再討論第二個例子。隨機塊模型是關於社區的模型。假設再$n$個人中有$k$個社區$C_{1}, C_{2}, \ldots, C_{k}$。假設兩個人在同一社區認識對方的概率為$p$,在不同社區認識對方的概率為$q$,其中,$q<p$。假設事件人$i$認識人$j$是互相獨立的。具體地,我們給出$n\times n$數據矩陣,其中$a_{ij}=1$當且僅當$i$和$j$彼此認識。可以將A視為圖的鄰接矩陣。在實際中,圖形相當稀疏,即$p$和$q$很小,即$O(1 / n)$ or $O(\ln n / n)$。
考慮簡單情形:兩個社區各有$n/2$個人,且$p=\frac{\alpha}{n} \quad q=\frac{\beta}{n} \quad$ ,其中$\alpha, \beta \in O(\ln n)$。令$\mathbf{u}$和$\mathbf{v}$分別為社區一和二的數據點的質心,所以$u_{i} \approx p$ for $i \in C_{1}$和 $u_{j} \approx q$ for $j \in C_{2}$ 並且$v_{i} \approx q$ for $i \in C_{1}$ 和$v_{j} \approx p$ for $j \in C_{2}$。我們有
$$
|\mathbf{u}-\mathbf{v}|^{2}=\sum_{j=1}^{n}\left(u_{j}-v_{j}\right)^{2} \approx \frac{(\alpha-\beta)^{2}}{n^{2}} n=\frac{(\alpha-\beta)^{2}}{n}
$$
$$Inter-centroid distance\approx \frac{\alpha-\beta}{\sqrt{n}}$$
我們要求$\|A-C\|_{2}$的上界。這是非平凡的,因為我們必須對所有單位向量$\mathbf{v}$證明一個統一的上界。隨機矩陣(RMT)理論已經為我們做了這個。RMT告訴我們$$
\|A-C\|_{2} \leq O^{*}(\sqrt{n p})=O^{*}(\sqrt{\alpha})
$$
因此,只要$\alpha-\beta \in \Omega^{*}(\sqrt{\alpha})$,我們有$\Omega(1)$標準差分離的均值,從而譜聚類工作。
### 4、拉普拉斯算子
譜聚類的一個重要特例是當$k=2$時。如果我們一個算法將數據分成兩部分,這可以遞歸的應用。一種使用該譜算法的情形是應用在圖的拉普拉斯矩陣L上,其被定義為
$$L=D-A$$
其中$A$是鄰接矩陣,$D$是自由度的對角矩陣。我們令$A$為負號。
對任意向量$x$,我們有
$$
\mathbf{x}^{T} L \mathbf{x}=\sum_{i} d_{i i} x_{i}^{2}-\sum_{(i, j) \in E} x_{i} x_{j}=\frac{1}{2} \sum_{(i, j) \in E}\left(x_{i}-x_{j}\right)^{2}
$$
由於$L$的所有行和為0,因此其最小特征值為0,對應的特征向量為$\mathbf{1}$。所有數據點對此向量的投影點僅僅是原點,因此不能提供任何信息。如果我們采用第二低的奇異向量並進行投影,我們得到非常簡單的將$n$個實數進行聚類的問題。
Clustering ,翻譯為"聚類",就是把相似的東西分為一組,同 Classification(分類)不同, classifier 從訓練集中進行"學習",從而能夠對未知數據進行分類,這種提供訓練數據的過程叫做 supervised learning (監督學習),而在聚類的時候,我們並不關心某一類是什麽,我們只需要把相似的東西聚到一起,因此,一個聚類算法通常只需要知道如何計算相似度就可以工作了,因此 clustering 通常並不需要使用訓練數據進行學習,這在 Machine Learning 中被稱作 unsupervised learning (無監督學習)。 ## 一、聚類的兩種常用的假設
$$
\Phi_{k c e n t e r}(\mathcal{C})=\max _{j=1} \max _{\mathbf{a}_{i} \in C_{j}} d\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
$$
例如,消防站位置問題(最小化消防站可能需要前往的最大距離)。
2. **k-median clustering:** 最小化數據點到其中心的距離之和,即minimize$$
$$
k-median比k-center更具有抗噪性,因為少數異常值通常不會更改最佳解決方案。
3. **k-means clustering:** 最小化數據點到其中心的距離平方和,即mminimize$$
\Phi_{k m e a n s}(\mathcal{C})=\sum_{j=1}^{k} \sum_{\mathbf{a}_{i} \in C_{j}} d^{2}\left(\mathbf{a}_{i}, \mathbf{c}_{j}\right)
k-means比k-median更重視異常值,因為對距離進行了平方,這會放大大的值。 當數據由$R^d$中的點組成時,更常使用k-means準則,而當我們具有有限度量時,k-median更常用,即數據是具有邊距離的圖中的節點。
### 2、高密度聚類
如果我們不相信我們的聚類是基於中心的,那麽通常做出的的另一個假設是聚類由高密度區域組成,他們之間是低密度的“護城河”。

## 二、k-Means Clustering
### 1、動機
考慮使用k-means準則的最大似然動機。假設我們的數據是由k個良好分離的球形高斯密度等權混合生成的,這k個高斯密度的均值分別為$\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$,方差都為1。從而混合分布的密度為$$
\operatorname{Prob}(\mathrm{x})=\frac{1}{(2 \pi)^{d / 2}} \frac{1}{k} \sum_{i=1}^{k} e^{-\left|\mathrm{x}-\mu_{i}\right|^{2}}
$$
定義最接近x的中心為$\mu(x)$,由於指數函數快速下降,我們可以用$e^{-|\mathbf{x}-\boldsymbol{\mu}(\mathbf{x})|^{2}}$近似$\sum_{i=1}^{k} e^{-\left|\mathbf{x}-\boldsymbol{\mu}_{i}\right|^{2}}$。因此,$$
\operatorname{Prob}(\mathbf{x}) \approx \frac{1}{(2 \pi)^{d / 2} k} e^{-|\mathbf{x}-\mu(\mathbf{x})|^{2}}
$$
從而,從混合分布中選擇樣本點的可能性為$$
\frac{1}{k^{n}} \frac{1}{(2 \pi)^{n d / 2}} \prod_{i=1}^{n} e^{-\left|\mathbf{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}=c e^{-\sum_{i=1}^{n}\left|\mathrm{x}^{(\mathrm{i})}-\mu\left(\mathrm{x}^{(\mathrm{i})}\right)\right|^{2}}
$$
因此,最小化到聚類中心的距離平方和得到最大似然 $\mathbf{\mu}_2, \mathbf{\mu}_2, \dots, \mathbf{\mu}_k$。
### 2、k-means目標的性質
**引理2.1** 當x是質心時,數據點到x的距離平方和得到最小化,即$\mathbf{x}=\frac{1}{n} \sum_{i} \mathbf{a}_{\mathbf{i}}$。
**證明**:我們的目標是尋找x,最小化$\sum_{i}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{x}\right|^{2}$。通過簡單計算可得
$$
\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{x}\right|^{2}=\sum_{i}\left|\mathrm{a}_{\mathrm{i}}-\mathrm{c}\right|^{2}+n|\mathrm{c}-\mathrm{x}|^{2}
$$等式右邊第一部分是確定的數,第二部分最小值為0,在$x=c$處取得。
### 3、Lloyd‘s Algorithm
k-means聚類一個常用的算法是Lloyd‘s Algorithm。
**Lloyd‘s Algorithm:**
1. 初始化k個中心(隨機選擇?);
2. 將每個點與最靠近它的中心聚類;
3. 找到每個聚類的質心作為新中心替換舊中心;
4. 重復Step 2和Step 3直到聚類中心收斂(根據一些準則,例如k-means得分不再提高) Lloyd算法不一定能找到全局最優解,但會找到局部最優解。算法中一個重要的步驟是初始化。下面的例子說明了初始中心會顯著影響聚類結果。

上圖中有三個密集簇,分別以$(0,1),(0,-1)$和$(3,0)$為中心。但如果我們以一個中心$(0,1)$和兩個接近$(3,0)$的中心初始化,那麽$(0,1)$處的中心會移到$(0,0)$,而$(3,0)$處的兩個中心會呆在那裏,將這一簇分成兩部分。 因此,對於初始中心的選擇要遵循一定的策略。最常用的策略為“最遠遍歷”。首先選擇一個數據點作為初始中心$c_1$,然後選擇距離$c_1$最遠的數據點作為$c_2$,然後選擇距離$\{c_1,c_2\}$最遠的數據點作為$c_3$,等等。直到選足了k個點,將它們用作初始中心。註意到,這樣可以在圖7.2中得到正確的聚類。 “最遠便利”會被少數異常值欺騙。k-means++對此進行改進,基於它們與已挑選中心的距離來加權數據點,具體而言,與距離平方成比例。然後根據這些權重概率地選擇下一個中心。另一種方法是為k-means問題運行一些其他近似算法,然後使用其輸出作為Lloyd算法的起點。 ### 4、Ward‘s Algorithm
從它自己的簇中的每個數據點開始,然後重復的合並成對的簇,直到只剩下k個簇。具體來說,Ward算法合並了最小化k-means成本增量的兩個簇,即合並 $\left(C, C^{\prime}\right)$ minimizing
$$
\operatorname{cost}\left(C \cup C^{\prime}\right)-\operatorname{cost}(C)-\operatorname{cost}\left(C^{\prime}\right)
$$
### 4、一維中的k-Means聚類
假設已經得到了$a_{1}, \dots, a_{i}$的所有最優k‘-means聚類($\forall k‘\le k$), 要計算$a_{1}, \dots, a_{i+1}$的最優k‘-means聚類,即尋找$j$,最小化
$$dist(a_1,\cdots,a_{j-1})+dist(a_j,\cdots,a_{i+1})$$
前者聚成$k‘-1$類,後者聚成1類。 對於給定的$i$,我們需要計算$k‘=1,\cdots,k$,每次計算$a_{1}, \dots, a_{i}$的k‘-means聚類時,需要運行$i$個$j$($i\le n$)。因此運行時間為$O(kn)$。而一共有$n$個$i$,因此總的運行時間為$O(kn^2$)。 ## 三、k-Center Clustering
將任意點到聚類中心的最大距離稱為聚類的半徑。存在半徑為r的k聚類當且僅當存在k個半徑為r的球體將所有的點覆蓋。下面,我們給出一個簡單的算法來尋找k個球覆蓋所有點。
**The Farthest Traversal k-clustering Algorithm** 1. 任意選擇一個點作為第一個聚類中心;
2. 對$t=2,3,\cdots,k$,選擇距離當前聚類中心最遠的點,作為第$t$個聚類中心。 該算法相當於初始化Lloyd算法的最遠遍歷策略。下面的引理表明該算法僅需要使用最多為最佳k-center解的兩倍的半徑。
**Theorem 7.3** 如果存在半徑為$\frac{r}{2}$的$k$聚類,那麽上面的算法找到的$k$聚類的半徑至多為$r$。
**證明**:若不然,即存在數據點$x$,它距離所有中心$>r$ $\Rightarrow$ 每次產生的新中心距離當前中心$>r$ (否則它就不是距離當前中心最遠的點,因為$x$距離當前中心$>r$ )。從而,$k$個中心加上一個數據點$x$,共有$k+1$個數據點,它們的距離成對的比$r$更大。但在半徑為$\frac{r}{2}$的$k$聚類中,沒有兩個這樣的點可以屬於同一簇,矛盾。
## 四、Spectral Clustering(譜聚類)
Spectral Clustering 其實就是通過 Laplacian Eigenmap 的降維方式降維之後再做 K-means 的一個過程。
譜聚類遵循以下步驟: - 尋找由A的前k個右奇異向量生成的空間V
- 將數據點投影到V上
- 對投影點聚類
### 1、為什麽要投影?
投影會使數據點更接近其聚類中心。

令數據矩陣$A$的第$i$行表示第$i$個數據點,C的第$i$行表示第$i$個數據點屬於的中心點。(對於$k$聚類問題有且僅有$k$個不同行)那麽,數據點到其聚類中心的距離平方和為
$$
\sum_{i=1}^{n}\left|\mathbf{a}_{\mathbf{i}}-\mathbf{c _ { i }}\right|^{2}=\|A-C\|_{F}^{2}
$$
通過聚類能夠將到聚類中心的距離平方和由$\|A-C\|_{F}^{2}$減小到投影中的8$k\|A-C\|_{2}^{2}$.。
**Theorem 7.4** 對任意秩小於等於k的矩陣$C$,有
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k\|A-C\|_{2}^{2}
$$
**證明**:$$rank(A_k-C)\le rank(A_k) + rank(C)\le k+k=2k$$
由於$\|A\|_{2}^{2} \leq\|A\|_{F}^{2} \leq k\|A\|_{2}^{2}$,所以
$$
\left\|A_{k}-C\right\|_{F}^{2} \leq 2 k\left\|A_{k}-C\right\|_{2}^{2}
$$
又
$$
\left\|A_{k}-C\right\|_{2} \leq\left\|A_{k}-A\right\|_{2}+\|A-C\|_{2} \leq 2\|A-C\|_{2}
$$
得證。
### 2、算法
定義$\sigma(C)=\|A-C\|_{2} / \sqrt{n}$。
**Spectral Clustering - The Algorithm**
- 尋找A的前k個奇異值向量,然後將A的列投影到由這向量生成的空間上,得到$A_k$;
- 從$A_k$中選擇一行進行聚類,使得$A_k$的所有行與該行的距離都小於$6k \sigma(C) / \varepsilon$;
- 重復Step 2 $k$次。 **Theorem 7.5** 如果在$k$聚類$C$中,每對中心間隔至少15$k \sigma(C) / \varepsilon$,並且每一類中至少有$\varepsilon n$個點,則以至少$1-\varepsilon$的概率,譜聚類找到的聚類$C‘$與$C$至多有$\varepsilon^{2} n$個點不同。
**證明**:首先證明對大多數的數據點,數據點的投影與其聚類中心的距離在$3k \sigma(C) / \varepsilon$以內。令
$$
M=\left\{i :\left|\mathbf{v}_{\mathrm{i}}-\mathbf{c}_{\mathrm{i}}\right| \geq 3 k \sigma(C) / \varepsilon\right\}
$$
其中$\mathbf{v}_i$表示$A_k$的第$i$行。下面證明$|M|$是小的。
由於$\left\|A_{k}-C\right\|_{F}^{2}=\sum_{i}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq \sum_{i \in M}\left|\mathrm{v}_{\mathrm{i}}-\mathrm{c}_{\mathrm{i}}\right|^{2} \geq|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}}$,所以,由定理7.4,有
$$
|M| \frac{9 k^{2} \sigma^{2}(C)}{\varepsilon^{2}} \leq\left\|A_{k}-C\right\|_{F}^{2} \leq 8 k n \sigma^{2}(C) \quad \Longrightarrow \quad|M| \leq \frac{8 \varepsilon^{2} n}{9 k}
$$
如果$i \notin M$,稱數據點$i$是好的。對於屬於同一簇的兩個好點$i$和$j$,由於它們的投影與中心距離在$3k \sigma(C) / \varepsilon$以內,所以兩個點的投影距離在$6k \sigma(C) / \varepsilon$以內。另一方面,對於屬於不同簇的兩個好點$i$和$k$,由於兩個簇的中心間隔至少15$k \sigma(C) / \varepsilon$,所以兩個點的投影距離一定比$15 k \sigma(C) / \varepsilon-6 k \sigma(C) / \varepsilon=9 k \sigma(C) / \varepsilon$大。因此,如果我們在Step 2中選擇了一個好點(如點$i$),那麽我們算法放置在它的簇中的好點就確為與$i$在同一簇中的好點。因此,如果在Step 2的第k次執行中,我們選擇了一個好點,那麽所有好點都被正確聚類。又由於$|M| \leq \varepsilon^{2} n$,定理即成立。
為了完成證明,,我們還需說明Step 2中選擇壞點的可能性很小。有上面證明,可知每一類中好點的個數至少$(\varepsilon-\varepsilon^2)n$。因此,從每一類中挑出好點的概率至少為$(\varepsilon-\varepsilon^2)n/(\varepsilon n)=1-\varepsilon$。
### 3、由$\Omega(1)$標準差分離的均值
對於實線上的概率分布,“由$6$標準差分離的均值”足夠區分不同的分布。如果$k \in O(1)$並且$6$被一些常數代替,則譜聚類能夠使我們在更高維度上做同樣的事。首先定義標準偏差為數據點到聚類中心的平方均值在所有單位方向$\mathrm{v}$上的最大值,即
$$
\sigma(C)^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1} \sum_{i=1}^{n}\left[\left(\mathbf{a}_{\mathbf{i}}-\mathbf{c}_{\mathbf{i}}\right) \cdot \mathbf{v}\right]^{2}=\frac{1}{n} \max\limits_{|\mathbf{v}|=1}|(A-C) \mathbf{v}|^{2}=\frac{1}{n}\|A-C\|_{2}^{2}
$$
這也與我們之前對$\sigma(C)$的定義相同。
現在,很容易看出Theorem 7.5可以重新表述(假設$k \in O(1)$)為 - 如果$C$中的聚類中心可以由$\Omega(\sigma(C))$分離,那麽譜聚類算法找到的聚類$C‘$與$C$只有很小一部分數據點不同。 可以看出,對於許多隨機模型,“均值由$\Omega(1)$標準差分離”條件成立。在這裏用兩個例子說明。 首先,假設我們有$k \in O(1)$個球面高斯的混合,其標準差均為1。數據由這個混合產生。如果高斯的均值是$\Omega(1)$分離的,那麽條件“均值由$\Omega(1)$標準差分離”是滿足的,因此當我們投影到SVD子空間並聚類,我們將得到(接近)正確的聚類。 我們再討論第二個例子。隨機塊模型是關於社區的模型。假設再$n$個人中有$k$個社區$C_{1}, C_{2}, \ldots, C_{k}$。假設兩個人在同一社區認識對方的概率為$p$,在不同社區認識對方的概率為$q$,其中,$q<p$。假設事件人$i$認識人$j$是互相獨立的。具體地,我們給出$n\times n$數據矩陣,其中$a_{ij}=1$當且僅當$i$和$j$彼此認識。可以將A視為圖的鄰接矩陣。在實際中,圖形相當稀疏,即$p$和$q$很小,即$O(1 / n)$ or $O(\ln n / n)$。
考慮簡單情形:兩個社區各有$n/2$個人,且$p=\frac{\alpha}{n} \quad q=\frac{\beta}{n} \quad$ ,其中$\alpha, \beta \in O(\ln n)$。令$\mathbf{u}$和$\mathbf{v}$分別為社區一和二的數據點的質心,所以$u_{i} \approx p$ for $i \in C_{1}$和 $u_{j} \approx q$ for $j \in C_{2}$ 並且$v_{i} \approx q$ for $i \in C_{1}$ 和$v_{j} \approx p$ for $j \in C_{2}$。我們有
$$
|\mathbf{u}-\mathbf{v}|^{2}=\sum_{j=1}^{n}\left(u_{j}-v_{j}\right)^{2} \approx \frac{(\alpha-\beta)^{2}}{n^{2}} n=\frac{(\alpha-\beta)^{2}}{n}
$$
$$Inter-centroid distance\approx \frac{\alpha-\beta}{\sqrt{n}}$$
我們要求$\|A-C\|_{2}$的上界。這是非平凡的,因為我們必須對所有單位向量$\mathbf{v}$證明一個統一的上界。隨機矩陣(RMT)理論已經為我們做了這個。RMT告訴我們$$
\|A-C\|_{2} \leq O^{*}(\sqrt{n p})=O^{*}(\sqrt{\alpha})
$$
因此,只要$\alpha-\beta \in \Omega^{*}(\sqrt{\alpha})$,我們有$\Omega(1)$標準差分離的均值,從而譜聚類工作。
### 4、拉普拉斯算子
譜聚類的一個重要特例是當$k=2$時。如果我們一個算法將數據分成兩部分,這可以遞歸的應用。一種使用該譜算法的情形是應用在圖的拉普拉斯矩陣L上,其被定義為
$$L=D-A$$
其中$A$是鄰接矩陣,$D$是自由度的對角矩陣。我們令$A$為負號。
對任意向量$x$,我們有
$$
\mathbf{x}^{T} L \mathbf{x}=\sum_{i} d_{i i} x_{i}^{2}-\sum_{(i, j) \in E} x_{i} x_{j}=\frac{1}{2} \sum_{(i, j) \in E}\left(x_{i}-x_{j}\right)^{2}
$$
由於$L$的所有行和為0,因此其最小特征值為0,對應的特征向量為$\mathbf{1}$。所有數據點對此向量的投影點僅僅是原點,因此不能提供任何信息。如果我們采用第二低的奇異向量並進行投影,我們得到非常簡單的將$n$個實數進行聚類的問題。
【Foundation of data science】Clustering
