本文記錄一些對深度學習的思考總結.意識流寫法，想到哪寫到哪，日後不定期更新補充.

在沒有接觸深度學習的時候，覺得這是個非常高大上的技術，數學基礎要求非常多,上手門檻非常高.我想很多人和我有一樣的想法.這種對深度學習的印象，我想很大一部分來自鋪天蓋地的自媒體的有關AI的報道解讀,造成了一種深度學習,人工智慧非常高大上的感覺. 實際上媒體人沒有相關的理論基礎，甚至沒有工科背景,文章寫出來又要吸引人能帶流量，有時又難免誇大，各種名詞什麼神經網路，人工智慧，梯度爆炸，平行計算優化，對沒有接觸過相關技術的人來說，很容易造成一種很高大上很神祕的印象.

其實，神經網路並不是什麼新鮮的東西,早幾十年就有了，卷積也不是什麼新鮮東西，在模式識別，影象處理裡也早就應用廣泛. 現如今，深度學習大紅大紫，還是因為時代發展到了這個階段，算力的發展，晶片的發展，更快的gpu的出現，更好的計算優化技術,網際網路時代我們有了大量的資料，這些都使得卷積神經網路的訓練成為可能，而不是僅僅在理論層面.大量的訓練資料，使得深度學習在很多業務領域有了更好的表現，尤其是影象處理方面。

深度學習的本質

先說結論：本質就尋找最合適的卷積核，最合適的特徵權重，最大限度擬合訓練樣本。本質是計算。

以影象處理為例，傳統的方法怎麼做的？ 手工提取特徵 + 傳統機器學習. 深度學習怎麼做的？端到端的學習,不再需要手工提取特徵了，自己學習特徵.
比如下面這幅圖,你很容易就認出來這是一隻貓.

你有沒有想過，你的大腦是怎麼識別出來這是一隻貓的？通過眼睛，耳朵，嘴巴，尾巴，腿？還是通過這些的組合？這裡的"耳朵，嘴巴，尾巴"等等就是所謂的"特徵"。雖然你並沒有意識到你的大腦經過了一系列複雜的運算，但它確實是經過了一系列複雜的運算，然後告訴你這是一個貓。只不過神經元的速度太快了，你意識不到而已.

對計算機而言,上面的圖就是一堆數字而已，比如800*600的圖，就是一個800*600*3的矩陣，為了簡化表達,就用灰度圖來說吧,那就是800*600的矩陣，矩陣裡相應元素的值代表著畫素值.當然"畫素值"這個概念，也是我們人為賦予的,計算機才不care什麼畫素值不畫素值,對它來說,就是個數字而已.

那問題來了，什麼樣的數字代表"貓的眼睛"，什麼樣的數字代表"貓的耳朵"？以前這個工作是手工去做的.現在是神經網路自動去做的.
比如對連續5個畫素，值為1,34,67,89,213，我就認為這5個畫素代表貓頭，這個規則是我事先定義好的.（當然這是我瞎定義的，這5個畫素當然不能代表貓頭）。手工去做的時候，你需要理解業務，比如識別車和識別貓，（1,34,67,89,213）在貓的圖片裡可能代表貓頭，在車子圖片裡可能代表車屁股,其含義是不同的.這就麻煩了,不同的領域，規則不同，而且，特徵工程就是他孃的玄學啊,特徵成千上萬，找也找不完，好的特徵和壞的特徵對最後的識別結果帶來的影響千差萬別，怎麼衡量該重點考慮哪種特徵？.

而對深度學習來說，輸入就是一堆數字而已，它不懂數字代表的業務含義，它也不需要懂，它只要嘗試出最合適的卷積矩陣，使得loss最小就行，前面也說了，本質是計算。

這裡也可以看到，傳統的方法和深度學習的方法，在思路上就是完全兩種思路. 前者更看著規則的定義,也就是特徵的提取. 後者則更看重輸入的資料,只要你輸入的資料夠多，質量夠好,我就能自動提取出有效的特徵和權重.(當然,這個意義也是我們人為賦予的,學習出來的其實就是一堆數而已,我們把他們稱之為特徵,這個時候,他們不再代表貓頭、耳朵等等了,可能就是一個點,一條線,肉眼看去已經無法理解了,如下圖)

這也是前面提到的，深度學習之所以站到了歷史的臺前的兩大原因之一：海量的資料。

現在就涉及到卷積的概念了.

卷積

為什麼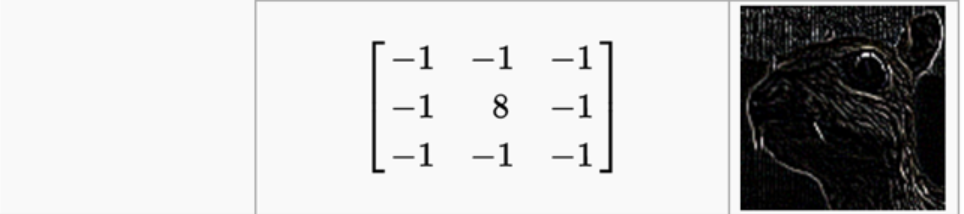
這個卷積核能起到邊緣檢測的作用？想想你是怎麼去判斷影象邊緣的？如果給你一副純色圖,有邊緣嗎？
比如
顯然沒有啊。因為純色圖,矩陣的每一個畫素值都一樣的,所以分不出邊緣.看出來了吧,你通過判斷與周邊畫素的差別來判斷是不是邊緣.差別越大越有可能是邊緣.現在在看上面的卷積核,很清楚了吧,經過卷積運算（不懂卷積運算的,先看看置頂的那篇https://www.cnblogs.com/sdu20112013/p/10149529.html） .每一個畫素值x都變成了8*x + (-1)*周邊畫素，即8*x -周邊畫素。這可不就是在比較當前畫素和周邊畫素的差值嗎？所以卷積完的矩陣,繪圖繪製出來,就有了邊緣的效果.

按照這個思路,不難理解為什麼不同的卷積核會有不同的效果了,也就是不同的特徵被我們提取出來了.很多人設計好了很多卷積核,分別完成不同的功能.傳統的影象處理,就是去使用這些卷積核,再配以規則,完成適配自己業務領域資料的特徵提取.

好,重點來了.上面說了,"邊緣"這個特徵被提取出來了,那對這個代表影象邊緣的矩陣，叫matrix_a吧,繼續找一個卷積矩陣kenerl_a,對其做卷積,得到matrix_b，這個martrix_b什麼意義呢？再對這個martrix_b做卷積,得到martrix_c,這個martix_c又代表啥呢？答案是我們不知道,像上面提到的,最終的矩陣繪製出來,可能已經是一個點,一條線了，我們已經無法肉眼識別他們在現實世界的對應物體了.但並不代表這是無意義的,不同於貓的眼睛,耳朵等等這些高階特徵,這時候得到的這些點啊線啊,已經是非常抽象的低階特徵了.而圖片正是由這些大量的低階特徵組成的.

深度學習乾的啥事？就是尋找成千上萬的卷積核,得到成千上萬的特徵,然後用分類也好,迴歸也罷,認為我們的目標=特徵權重*特徵之和.比如obj=0.3*feature1 + 0.5*feature2,obj=1代表貓,obj=2代表狗. 這樣拿到一個新的圖片,輸入給模型,模型通過卷積就計算出對應的feature1，feature2，然後計算obj，然後我們就知道了這張圖是貓和狗.

當然,卷積核不是瞎找的,卷積核矩陣裡面的數字到底填幾，要是一個個瞎試,再牛逼的gpu，再牛逼的晶片也試不完啊.這裡面就涉及到損失函式定義,梯度下降了.
詳細的去看我機器學習的文章吧,不想看的就知道模型學習的過程裡,卷積核的值填什麼不是隨機亂填的,每次反向傳播更新卷積核的時候都是朝著讓loss更小,也就是讓模型更準確（所謂更準確,是針對你的訓練資料來說的，同樣的網路結構,你機器上跑出來的模型的引數和別人跑出來的模型引數是不一樣的，如果你們的訓練資料不一樣的話）這樣一個目標去更新的就完了.

怎麼設計出一種濾波器/卷積核

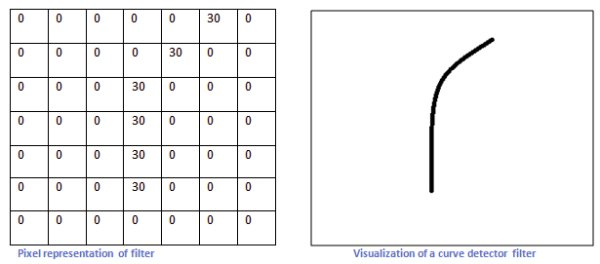
比如上圖的卷積核可以識別右邊的曲線.道理也是很顯然的,上圖的卷積核的形狀就是類似我們想要的曲線的形狀的.如果遇到類似形狀的影象,卷積(對應位置畫素值相乘再相加)之後得到的數會很大,反之很小.這樣就把想要的形狀的曲線識別出來了.

與訊號處理的關係

大學的時候,學訊號處理,天天就是各種傅立葉變換,完全不知道有啥用.說實在的,大學的很多老師水平其實也不咋地,基本就是照本宣科,要麼放萬年不變的PPT,可能自己都不能深刻理解，或者與產業界太脫離,完全不講這些理論的現實應用.其實講清楚這些現實意義也沒那麼難麼.所以還在上學的同學們,要好好學習啊，要好好學習啊，要好好學習啊，重要的事情說三遍,你現在以為沒用的東西,不知道哪天就派上用場了.

現在回頭看,卷積不就是離散的傅立葉變換嗎. 從訊號的角度理解卷積，卷積核不就是濾波器嗎,卷積核對影象的作用,不就是對影象這種訊號做濾波嗎.啥叫濾波,其實也就是特徵提取。
傅立葉變換將時域和空域資訊-->轉換到頻域上. 對影象處理而言,我們處理的大部分時候是空域的資訊.說人話就是空間資訊,對單幀影象而言,我們卷積出來的特徵,點也好,線也罷，是一種形狀,是空間上的資訊. 連續的影象才存在這時間資訊,多幀影象是有聯絡的,比如視訊,時域資訊就很重要了.

https://www.zhihu.com/question/20099543/answer/13971906

首先說說影象頻率的物理意義。影象可以看做是一個定義為二維平面上的訊號，該訊號的幅值對應於畫素的灰度（對於彩色影象則是RGB三個分量），如果我們僅僅考慮影象上某一行畫素，則可以將之視為一個定義在一維空間上訊號，這個訊號在形式上與傳統的訊號處理領域的時變訊號是相似的。不過是一個是定義在空間域上的，而另一個是定義在時間域上的。所以影象的頻率又稱為空間頻率，它反映了影象的畫素灰度在空間中變化的情況。例如，一面牆壁的影象，由於灰度值分佈平坦，其低頻成分就較強，而高頻成分較弱；而對於國際象棋棋盤或者溝壑縱橫的衛星圖片這類具有快速空間變化的影象來說，其高頻成分會相對較強，低頻則較弱（注意，是相對而言）。

影象的空間資訊丟掉了是什麼意思

先看CNN中全連線層引數是怎麼來的.參考https://zhuanlan.zhihu.com/p/33841176.

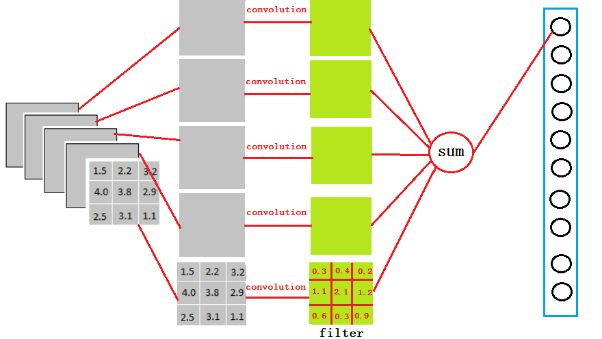
以VGG-16舉例,在VGG-16全連線層中,對224x224x3的輸入，最後一層卷積可得輸出為7x7x512，如後層是一層含4096個神經元的FC，則可用卷積核為7x7x512x4096的全域性卷積來實現這一全連線運算過程。

這樣做會有什麼好處和問題？

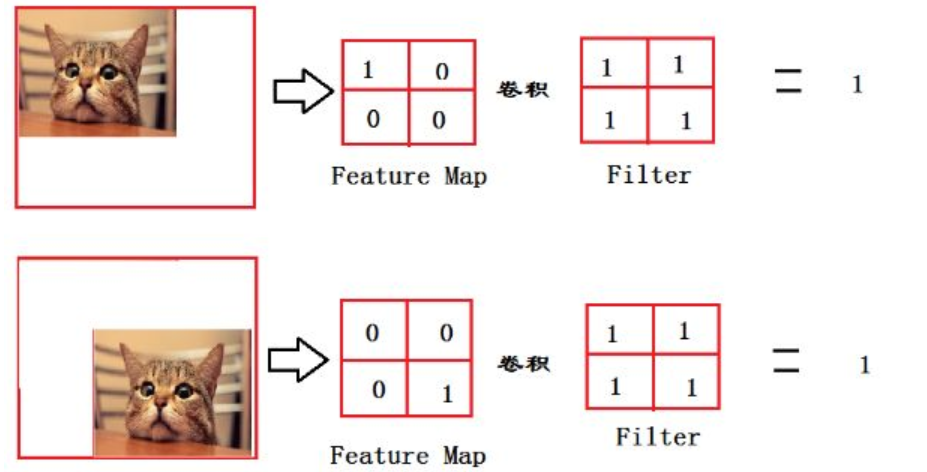
好處和壞處是一樣的,就是去除掉位置資訊的影響.主要看你處理的是什麼問題.對分類來說,我們不關心位置,希望某種畫素組合被識別為某種特徵,我們不在乎這種畫素組合在圖片矩陣的什麼位置出現,我都要能識別它,這時候就是好處.

但是對於影象分割來說,就是壞處了.因為我需要知道位置資訊.比如需要知道圖片裡的貓在左上角還是右下角，這樣才能準確分割.所以分割模型會用卷積層替代掉全連線層.

在我寫這篇文章的時候，我做了一點google,想看看有沒有人寫過類似的主題,發現有2篇文章寫的很好，我也引用了部分圖，推薦之。

• http://www.hankcs.com/ml/understanding-the-convolution-in-deep-learning.html
• https://blog.csdn.net/DL_CreepingBird/article/details/78574133