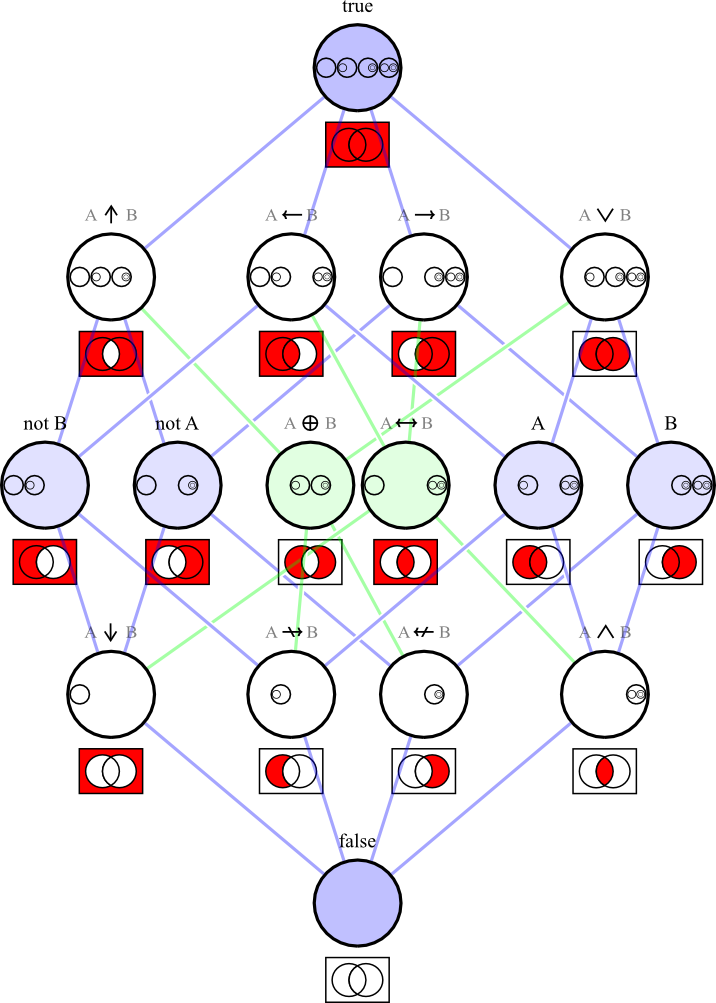
通過代數,數字,歐幾里得平面和分形討論JavaScript中的函數語言程式設計
本文是對函數語言程式設計正規化的系列文章從而拉開了與以下延續一個。
介紹
在JavaScript中,函式只是物件。因此,可以建構函式,作為引數傳遞,從函式返回或分配給變數。因此,JavaScript具有一流的功能。更準確地說,JavaScript支援以下內容:
- 高階函式引數
- 產生高階函式
- 巢狀函式
- 匿名功能
- 關閉
- 部分申請(ECMAScript 5)
通過函式表示資料
我們S是任何元素的集合a,b,c...(例如,桌子上的書本或歐幾里得平面的點),並讓S'是這些元素的任意子集(例如,桌子上的書本綠色或點半徑1的圓心以歐幾里德平面的原點為中心)。
所述特徵函式 S'(x)的一組S'
true或false與每個元件x的S。
S'(x) = true if x is in S' S'(x) = false if x is not in S'
讓我們S成為桌子上的一套書,讓我們S'成為桌上的綠色書籍。設a和b是兩個綠色的書,讓c和d是在表中的兩個紅本本。然後:
S'(a) = S'(b) = true S'(c) = S'(d) = false
讓S是集的歐幾里德平面中的點,並且讓S'在半徑為1的在歐幾里得平面(0,0)的原點為中心的圓的組的點的(單位圓)。讓a和b在單位圓的兩點,並讓c並且d是在歐幾里得平面的原點為中心的半徑2的圓的兩點。然後:
S'(a) = S'(b) = true S'(c) = S'(d) = false
因此,任何集合S'總是可以由其特徵函式表示。一個函式,它將一個元素作為引數,true如果該元素在S',false則返回,否則返回。換句話說,可以通過JavaScript中的函式表示集合(抽象資料型別)。
function set() { }
在接下來的部分中,我們將看到如何通過JavaScript以函式方式表示集合代數中的一些基本集合,然後我們將在集合上定義泛型二進位制運算。然後,我們將在歐幾里德平面的子集上對數字應用這些操作。集合是抽象資料結構,數字的子集和歐幾里得平面的子集是抽象資料結構的表示,最後二元操作是適用於抽象資料結構的任何表示的通用邏輯。
JavaScript環境
要執行網站原始碼,您需要一個JavaScript引擎。有很多JavaScript引擎可用。在本節中,我將逐步介紹如何使用Ubuntu 16.04中的V8 JavaScript引擎來設定JavaScript環境。V8是一個用C ++編寫的開源JavaScript引擎,用於谷歌Chrome,Node.js和V8.NET。設定也可以在Windows和macOS上完成。
- 獲取V8原始碼並編譯它:
我通過在終端中執行以下命令,在Ubuntu 16.04上成功安裝並執行了d8。
sudo apt-get install git mkdir ~/js cd ~/js git clone https://chromium.googlesource.com/chromium/tools/depot_tools.git depot_tools export PATH=~/js/depot_tools:"$PATH" fetch v8 cd v8 make native ~/js/v8/out/native/d8
從git儲存庫下載V8原始碼需要一些時間,具體取決於Internet連線速度。編譯V8原始碼也需要一些時間,具體取決於硬體配置,但在等待必要的時間後,一切正常。
- 我們可以編寫第一個JavaScript程式碼:
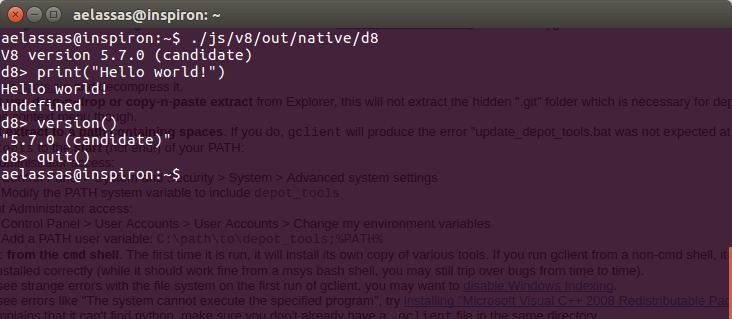
要在控制檯中載入JavaScript檔案,可以按如下方式執行:
load('set.numbers.demo.js')
集
本節通過JavaScript介紹集合代數中一些基本集的表示。
空集
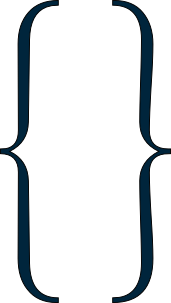
讓E是空集和Empty它的特色功能。在集合的代數中,E是沒有元素的唯一集合。因此,Empty可以定義如下:
Empty(x) = false if x is in E Empty(x) = false if x is not in E
因此,EJavaScript中的表示可以定義如下:
empty = function() {return function(){return false}}
在集合的代數中,Empty表示如下:
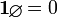
因此,執行以下程式碼:
print('\nEmpty set:')
print('Is 7 in {}? ' + empty()(7))
給出以下結果:
全部設定

我們S是一組和S'是的子集S,它包含所有要素,All其特色功能。在集合的代數中,S'是包含所有元素的完整集合。因此,All可以這樣定義:
All(x) = true if x is in S
因此,S'JavaScript中的表示可以定義如下:
all = function() {return function(){return true}}
在集合的代數中,All表示如下:
因此,執行以下程式碼:
print('\nSet All:')
print('Is 7 in integers set? ' + all()(7))
給出以下結果:

單身套裝
我們E是辛格爾頓集和Singleton它的特色功能。在集合的代數中,E也稱為單位集合,或者1元組是具有恰好一個元素的集合e。因此,Singleton可以定義如下:
Singleton(x) = true if x is e Singleton(x) = false if x is not e
因此,EJavaScript中的表示可以定義如下:
singleton = function(x) {return function(y){return x === y}}
因此,執行以下程式碼:
print('\nSingleton set:')
print('Is 7 in the singleton set {0}? ' + singleton(0)(7))
print('Is 7 in the singleton set {7}? ' + singleton(7)(7))
給出以下結果:

其他套裝
本節介紹整數集的子集。
偶數
我們E是一組連號,並且Even它的特色功能。在數學中,偶數是一個2的倍數。因此,Even可以定義如下:
Even(x) = true if x is a multiple of 2 Even(x) = false if x is not a multiple of 2
因此,EJavaScript中的表示可以定義如下:
even = function(x){return x%2 === 0}
因此,執行以下程式碼:
print('\nEven numbers set:')
print('Is 99 in even numbers set? ' + even(99))
print('Is 998 in even numbers set? ' + even(998))
給出以下結果:
奇數
我們E是一組奇數的和Odd它的特色功能。在數學中,奇數是一個不是2的倍數的數字。因此,Odd可以定義如下:
Odd(x) = true if x is not a multiple of 2 Odd(x) = false if x is a multiple of 2
因此,EJavaScript中的表示可以定義如下:
odd = function(x){return x%2 === 1}
因此,執行以下程式碼:
print('\nOdd numbers set:')
print('Is 99 in odd numbers set? ' + odd(99))
print('Is 998 in odd numbers set? ' + odd(998))
給出以下結果:
倍數為3
我們E是一組3的倍數和MultipleOfThree它的特色功能。在數學中,3的倍數是可被3整除的數。因此,MultipleOfThree可以定義如下:
MultipleOfThree(x) = true if x is divisible by 3 MultipleOfThree(x) = false if x is not divisible by 3
因此,EJavaScript中的表示可以定義如下:
multipleOfThree = function(x){return x%3 === 0}
因此,執行以下程式碼:
print('\nMultiples of 3 set:')
print('Is 99 in multiples of 3 set? ' + multipleOfThree(99))
print('Is 998 in multiples of 3 set? ' + multipleOfThree(998))
給出以下結果:
倍數為5
我們E是集合5的倍數和MultipleOfFive它的特色功能。在數學中,5的倍數是可被5整除的數。因此,MultipleOfFive可以定義如下:
MultipleOfFive(x) = true if x is divisible by 5 MultipleOfFive(x) = false if x is not divisible by 5
因此,EJavaScript中的表示可以定義如下:
multipleOfFive = function(x){return x%5 === 0}
因此,執行以下程式碼:
print('\nMultiples of 5 set:')
print('Is 15 in multiples of 5 set? ' + multipleOfFive(15))
print('Is 998 in multiples of 5 set? ' + multipleOfFive(998))
給出以下結果:
質數
很久以前,當我玩Project Euler問題時,我不得不解決以下問題:
By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13. What is the 10 001st prime number?
為了解決這個問題,我首先必須編寫一個快速演算法來檢查給定的數字是否為素數。編寫演算法後,我編寫了一個迭代演算法,迭代遍歷素數,直到找到10 001 st素數。
我們E是集合素數的和Prime它的特色功能。在數學中,素數是大於1的自然數,除了1和自身之外沒有正除數。因此,Prime可以定義如下:
Prime(x) = true if x is prime Prime(x) = false if x is not prime
因此,EJavaScript中的表示可以定義如下:
prime = function(x){
if(x===1) return false
if(x<4) return true
if(x%2===0) return false
if(x<9) return true
if(x%3===0) return false
var sqrt = Math.sqrt(x)
for(var i = 5; i <= sqrt; i+=6){
if(x%i===0) return false
if(x%(i+2)===0) return false
}
return true
}
因此,執行下面的程式碼來解決我們的問題:
print('\nPrimes set:')
print('Is 2 in primes set? ' + prime(2))
print('Is 4 in primes set? ' + prime(4))
print('The 10 001st prime number is ' + getPrime(10001))
其中getPrime定義如下:
getPrime = function(p){
var count = 0;
for(var i = 1; ; i++){
if(prime(i)) count++
if(count === p){
return i
break
}
}
}
給出以下結果:
二元操作
本節介紹了從給定集合和操作集合構造新集合的幾個基本操作。下面是集合代數中的維恩圖。
聯盟
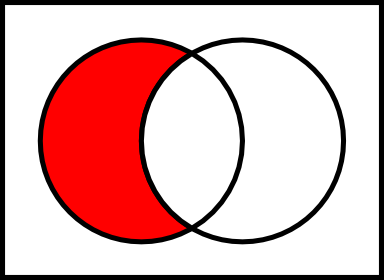
讓我們E和F兩套。該聯合的E和F,記為E U F是一組其是成員的所有元素E或F。
讓我們Union結合工會。因此,Union可以在JavaScript中按如下方式實現操作:
union = function(e, f){return function(x){ return e(x) || f(x)}}
執行以下程式碼:
print('\nUnion:')
print('Is 7 in the union of Even and Odd Integers Set? ' + union(even,odd)(7))
給出以下結果:

路口
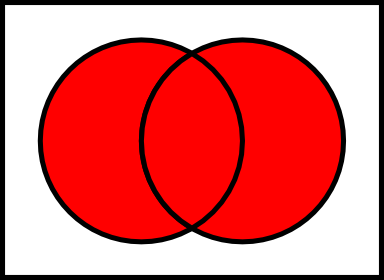
讓我們E和F兩套。的交叉點的E和F,記為E n F是一組這兩者都是成員的所有元素的E和F。
讓我們Intersection進行交叉操作。因此,Intersection可以在JavaScript中按如下方式實現操作:
intersection = function(e, f){return function(x){ return e(x) && f(x)}}
執行以下程式碼:
print('\nIntersection:')
multiplesOfThreeAndFive = intersection(multipleOfThree, multipleOfFive)
print('Is 15 a multiple of 3 and 5? ' + multiplesOfThreeAndFive(15))
print('Is 10 a multiple of 3 and 5? ' + multiplesOfThreeAndFive(10))
給出以下結果:

笛卡爾積

讓我們E和F兩套。的笛卡兒積的E和F,由表示E × F是該組所有有序對(e, f),使得e是其成員E和f是其成員F。
讓我們CartesianProduct進行笛卡爾積運算。因此,CartesianProduct可以在JavaScript中按如下方式實現操作:
cartesianProduct = function(e, f){return function(x, y){ return e(x) && f(y)}}
執行以下程式碼:
print('\nCartesian Product:')
cp = cartesianProduct(multipleOfThree,multipleOfFive)
print('Is (9, 15) in MultipleOfThree x MultipleOfFive? ' + cp(9, 15))
給出以下結果:
補語
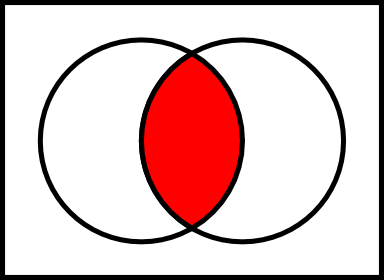
讓我們E和F兩套。的相對補的F中E,由表示E \ F是一組其是成員的所有元件的E但不是成員F。
讓我們Complement進行相對補充操作。因此,Complement可以在JavaScript中按如下方式實現操作:
complement = function(e, f){return function(x){ return e(x) && !f(x)}}
執行以下程式碼:
print('\nComplement:')
c = complement(multipleOfThree, multipleOfFive)
print('Is 15 in MultipleOfThree \\ MultipleOfFive set? '+ c(15))
print('Is 9 in MultipleOfThree \\ MultipleOfFive set? '+ c(9))
給出以下結果:
對稱差異
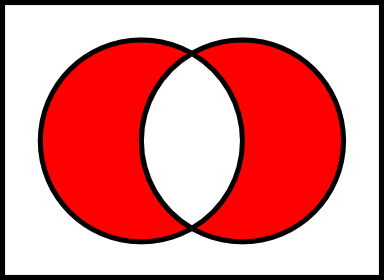
讓我們E和F兩套。的對稱差的E和F,記為E delta F是一組其是的任成員的所有元素的E和F,但不是在相交E和F。
讓我們SymmetricDifference進行對稱差分運算。因此,SymmetricDifference可以在JavaScript中以兩種方式實現該操作。一個簡單的方法是使用union和補充操作如下:
symmetricDifferenceWithoutXor = function(e, f){ return function(x)
{ return union(complement(e,f), complement(f, e))(x)}}
另一種方法是使用XOR二進位制操作如下:
symmetricDifferenceWithXor = function(e, f){return function(x)
{ return (e(x) ^ f(x)) === 1 ? true : false}}
執行以下程式碼:
print('\nSymmetricDifference without XOR:')
sdWithoutXor = symmetricDifferenceWithoutXor(prime, even)
print('Is 2 in the symetric difference of prime and even Sets? ' + sdWithoutXor(2))
print('Is 4 in the symetric difference of prime and even Sets? ' + sdWithoutXor(4))
print('Is 7 in the symetric difference of prime and even Sets? ' + sdWithoutXor(7))
print('\nSymmetricDifference with XOR:')
sdWithXor = symmetricDifferenceWithXor(prime, even)
print('Is 2 in the symetric difference of prime and even Sets? ', sdWithXor(2))
print('Is 4 in the symetric difference of prime and even Sets? ', sdWithXor(4))
print('Is 7 in the symetric difference of prime and even Sets? ', sdWithXor(7))
給出以下結果:
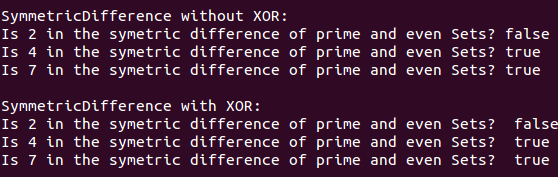
其他行動
本節介紹集合上其他有用的二進位制操作。
包含
設Contains是檢查元素是否在集合中的操作。此操作是一個函式,它將元素作為引數,true如果元素在集合中則返回,false否則返回。
因此,此操作在JavaScript中定義如下:
contains = function(e, x){return e(x)}
因此,執行以下程式碼:
print('\nContains:')
print('Is 7 in the singleton {0}? ' + contains(singleton(0), 7))
print('Is 7 in the singleton {7}? ' + contains(singleton(7), 7))
給出以下結果:
加
讓我們Add將一個元素新增到集合中的操作。此操作是一個函式,它將元素作為引數並將其新增到集合中。
因此,此操作在JavaScript中定義如下:
add = function(e, y){return function(x){ return x === y || e(x)}}
因此,執行以下程式碼:
print('\nAdd:')
print('Is 7 in {0, 7}? ' + add(singleton(0),7)(7))
print('Is 0 in {1, 0}? ' + add(singleton(1),0)(0))
print('Is 7 in {19, 0}? ' + add(singleton(19),0)(7))
給出以下結果:
去掉
設Remove是從集合中刪除元素的操作。此操作是一個函式,它將元素作為引數並將其從集合中刪除。
因此,此操作在JavaScript中定義如下:
remove = function(e, y){return function(x){ return x !== y && e(x)}}
因此,執行以下程式碼:
print('\nRemove:')
print('Is 7 in {}? ' + remove(singleton(0), 0)(7))
print('Is 0 in {}? ' + remove(singleton(7), 7)(0))
給出以下結果:
對於那些想要更進一步的人
您可以通過函數語言程式設計看到我們可以輕鬆地在JavaScript中使用集合代數。在前面的部分中,顯示了最基本的定義。但是,如果你想進一步,你可以考慮:
- 關係集
- 抽象代數,如么半群,群,場,環,K-向量空間等
- 包含 - 排除原則
- 羅素的悖論
- 康托爾的悖論
- 雙向量空間
- 定理和推論
歐幾里得飛機
在上一節中,集合的基本概念是在JavaScript中實現的。在本節中,我們將練習在平面點集(歐幾里德平面)上實現的概念。
繪製磁碟
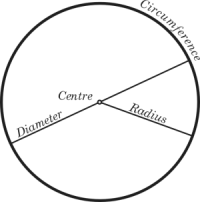
磁碟是由圓圈限定的平面的子集。有兩種型別的磁碟。封閉的磁碟是包含構成其邊界的圓的點的磁碟,而開啟的磁碟是不包含構成其邊界的圓的點的磁碟。
在本節中,我們將成立Characterstic功能的的封閉盤和HTML5繪製。
要設定Charactertic函式,首先需要一個計算平面中兩點之間歐氏距離的函式。該功能實現如下:
function distance(p1, p2){
return Math.sqrt(Math.pow(p1.x - p2.x, 2) + Math.pow(p1.y - p2.y, 2))
}
其中point定義如下:
point = function(x,y){
this.x = x
this.y = y
}
這個公式是基於畢達哥拉斯定理。
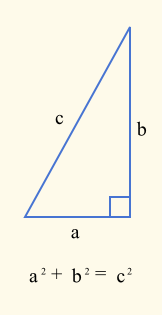
其中c是歐幾里德距離,a²是(p1.X - p2.X)²和b²是(p1.Y - p2.Y)²。
我們Disk是特色功能的封閉盤。在集合的代數中,實數集中的閉合磁碟的定義如下:
其中a和b是中心和R半徑的座標。
因此,DiskJavaScript中的實現如下:
disk = function(center, radius){return function(p){ return distance(p, center) <= radius}}
為了檢視集合,我決定實現一個draw在歐幾里得平面中繪製集合的函式。我選擇了HTML5,因此使用了canvas元素進行繪製。
因此,我通過該方法建立了下面說明的歐幾里德平面draw。
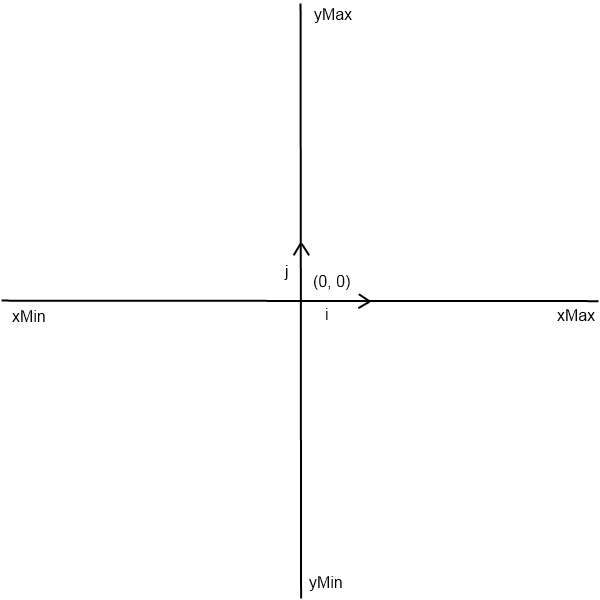
下面是飛機的實施。
/*
* Plane
*
*/
plane = function(width, height) {
/**
* Plane width in pixels
*
*/
this.width = width
/**
* Plane height in pixels
*
*/
this.height = height
/*
* Draws a generic set
*
*/
this.draw = function (set, canvasId){
var canvas = document.getElementById(canvasId)
canvas.width = this.width
canvas.height = this.height
var context = canvas.getContext('2d'),
semiWidth = this.width/2, semiHeight = this.height/2,
xMin = -semiWidth, xMax = semiWidth,
yMin = -semiHeight, yMax = semiHeight
for(var x = 0; x < this.width; x++){
var xp = xMin + x * (xMax - xMin) / this.width
for(var y = 0; y < this.height; y++) {
var yp = yMax - y * (yMax - yMin) / this.height
if(set(new point(xp, yp))) context.fillRect(x, y, 1, 1)
}
}
}
}
在該draw方法中,建立canvas具有與歐幾里德平面容器相同的寬度和相同高度的a 。然後(x,y),canvas如果屬於的是黑點,則每個畫素點都被替換為黑點set。xMin,xMax,yMin和yMax 是在的圖中所示的邊界值歐幾里得平面的上方。
執行以下程式碼:
euclideanPlane = new plane(200, 200) euclideanPlane.draw(disk(new point(0, 0), 50), 'disk')
這裡disk是id帆布:
<canvas id="disk">Your browser does not support HTML5 canvas.</canvas>
給出以下結果:
繪製水平和垂直半平面
甲水平或垂直半平面或者是兩個子集到其中的平面將歐幾里德空間。甲水平半平面或者是兩個子集到其中的平面垂直通過與所述的線劃分的歐幾里得空間的Y軸如上面的圖中。甲垂直半平面或者是兩個子集到其中的平面通過管線垂直與劃分歐幾里得空間的X軸。
在本節中,我們將設定水平和垂直半平面的特徵函式,在HTML5中繪製它們,看看如果我們將它們與磁碟子集組合,我們可以做些什麼。
我們HorizontalHalfPlane是特色功能一的水平半平面。HorizontalHalfPlaneJavaScript中的實現如下:
horizontalHalfPlane = function(y, isLowerThan){return function(p)
{ return isLowerThan ? p.y <= y : p.y >= y}}
因此,執行以下程式碼:
euclideanPlane.draw(horizontalHalfPlane(0, true), 'hhp')
這裡hhp是id帆布:
<canvas id="hhp">Your browser does not support HTML5 canvas.</canvas>
給出以下結果:
我們VerticalHalfPlane是特色功能一的垂直半平面。VerticalHalfPlaneJavaScript中的實現如下:
verticalHalfPlane = function(x, isLowerThan){return function(p) { return isLowerThan ? p.x <= x : p.x >= x}}
因此,執行以下程式碼:
euclideanPlane.draw(verticalHalfPlane(0, false), 'vhp')
這裡vhp是id帆布
<canvas id="vhd">Your browser does not support HTML5 canvas.</canvas>
給出以下原始碼結果:
在本文的第一部分中,我們在集合上設定了基本的二進位制操作。因此,通過組合a disk和a 的交集half-plane,我們可以繪製半盤子集。
因此,執行以下示例:
euclideanPlane.draw(intersection(disk(new point(0, 0), 50), verticalHalfPlane(0, false)), 'hd')
這裡hd是id帆布:
<canvas id="hd">Your browser does not support HTML5 canvas.</canvas>
給出以下結果:
功能
本節介紹歐幾里德平面上的集合的函式。
翻譯

我們translatePoint是翻譯在平面上的點的功能。在歐幾里德幾何中,translatePoint是一個將給定點在指定方向上移動恆定距離的函式。因此,JavaScript中的實現如下:
translatePoint = function(deltax, deltay){return function(p)
{ return new point(p.x + deltax, p.y + deltay)}}
其中(deltax, deltay)是翻譯的常量向量。
我們translate是轉化平面中的設定功能。這個函式在JavaScript中簡單地實現如下:
translate = function(e, deltax, deltay){return function(p)
{ return e(translatePoint(-deltax, -deltay)(p))}}
translate取deltax第一歐幾里德維度中的delta距離作為引數,其是deltay第二歐幾里德維度中的delta距離。如果點P(x,y)在集合S中被平移,則其座標將變為(x',y')=(x + delatx,y + deltay)。因此,點(X ' - delatx,Y' - DELTAY)將始終屬於集合小號。在集合代數中,translate稱為同構,換句話說,所有翻譯的集合形成翻譯組T,其與空間本身同構。這解釋了該功能的主要邏輯。
因此,執行以下程式碼:
var deltay = 0
setInterval(function(){
deltay = deltay <= euclideanPlane.height ? deltay + 20 : 0
euclideanPlane.draw(translate(disk(new point(0, -50), 50), 0, deltay) , 'ep_op')
}, 1000)
這裡ep_op是id帆布:
<canvas id="ep_op">Your browser does not support HTML5 canvas.</canvas>
給出以下結果:

位似
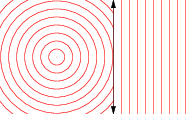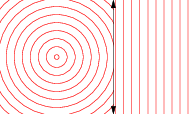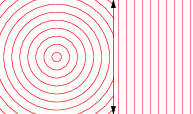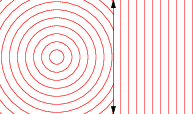
讓scalePoint是傳送的任何點的功能中號到另一點Ñ使得段SN是在同一行作為SM,而是由一個因子縮放拉姆達。在集的代數中,Scale表述如下:
因此,JavaScript中的實現如下:
scalePoint = function(lambdax, lambday, deltax, deltay)
{return function(p){ return new point(lambdax * p.x + deltax, lambday * p.y + deltay)}}
其中(deltax, deltay)是平移的常數向量,(lambdax, lambday)是lambda向量。
讓我們scale在計劃中的集合上應用同一性的功能。這個函式在JavaScript中簡單地實現如下:
scale = function(e, lambdax, lambday, deltax, deltay)
{return function(p){ return e(scalePoint(1/lambdax, 1/lambday,
-deltax/lambdax, -deltay/lambday)(p))}}
scale取deltax第一歐幾里德維度中的Δ距離作為引數,該第一歐幾里德維度deltay是第二歐幾里德維度中的Δ距離,並且(lambdax, lambday)是恆定因子向量λ。如果點P(x,y)scale在集合S中變換,則其座標將變為(x',y')=(lambdax * x + delatx,lambday * y + deltay)。因此,點((x'- delatx)/ lambdax,(y' - deltay)/ lambday)將始終屬於集合S,當然,如果lambda不同於向量0。在集合的代數中,scale稱為同構,換句話說,所有同態的集合形成Homothety組H,與空間本身\ {0}同構。這解釋了該功能的主要邏輯。
因此,執行以下程式碼:
var deltay = 0, lambday = 0.05
setInterval(function(){
deltay = deltay <= euclideanPlane.height ? deltay + 20 : 0
lambday = deltay <= euclideanPlane.height ? lambday + 0.05 : 0.05
euclideanPlane.draw(scale(disk(new point(0, -50), 50), 1, lambday, 0, deltay), 'ep_op')
}, 1000)
給出以下結果:

旋轉
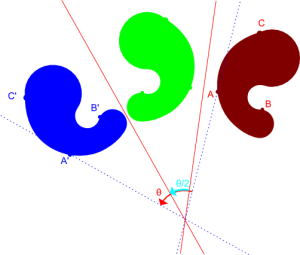
我們rotatePoint是用旋轉的角度2θ位置的點的功能。在矩陣代數中,rotatePoint表述如下:
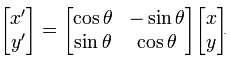
其中(x',y')是旋轉後點的座標,x'和y'的公式如下:
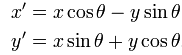
這個公式的演示非常簡單。看看這個輪換。
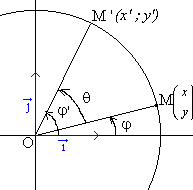
以下是演示:
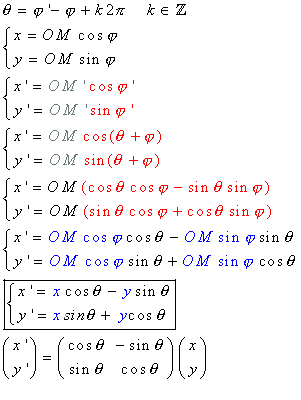
因此,JavaScript中的實現如下:
rotatePoint = function(theta){ return function(p)
{ return new point(p.x*Math.cos(theta)-p.y*Math.sin(theta),
p.x*Math.sin(theta)+p.y*Math.cos(theta))}}
我們rotate是在與角度theta平面一套適用的旋轉功能。這個函式在JavaScript中簡單地實現如下。
rotate = function(e, theta){ return function(p){return e(rotatePoint(-theta)(p))}}
rotate是一個作為引數的函式,theta它是旋轉的角度。如果點P(x,y)rotate在集合S中變換,那麼它的座標將變為(x',y')=(x * cos(theta) - y * sin(theta),x * sin( theta)+ y * cos(theta))。因此,點(X '* COS(THETA)+ Y' * SIN(THETA),Y '* COS(THETA) - X' * SIN(THETA))將永遠屬於一套小號。在集合的代數中,rotate稱為同構,換句話說,所有旋轉的集合形成旋轉組R,其與空間本身同構。這解釋了該功能的主要邏輯。
因此,執行以下程式碼:
var theta = 0
setInterval(function(){
euclideanPlane.draw(rotate(horizontalHalfPlane(-90, true), theta), 'ep_op')
theta = (theta + Math.PI/2)%(2*Math.PI)
}, 1000)
給出以下結果:

對於那些想要更進一步的人
很簡單,不是嗎?對於那些想要更進一步的人,你可以探索這些:
- 橢圓
- 三維歐氏空間
- Ellipsoide
- 拋物面
- 雙曲面
- 球諧波
- Superellipsoid
- 妊神星
- 同形體
- Focaloid
分形

分形是具有通常超過其拓撲維度並且可能落在整數之間的分形維數的集合。例如,Mandelbrot集是由一系列複數二次多項式定義的分形:
Pc(z) = z^2 + c
哪裡c是複雜的。所述曼德爾布羅分形被定義為所有點的集合c,使得上述序列不逃逸到無窮遠。在集合的代數中,這表達如下:
Fractals(抽象資料型別)總是可以在JavaScript中表示如下:
function fractal() {}
複數和繪圖
為了能夠繪製分形,我需要操縱複數。因此,我建立了complex以下類:
complex = function(r, i){
this.x = r
this.y = i
}
complex.prototype.toString = function(){
return this.x + ' + i * ' + this.y
}
complex.prototype.abs = function(){
return Math.sqrt(this.x*this.x+this.y*this.y)
}
complex.add = function(z1, z2){
return new complex(z1.x+z2.x, z1.y+z2.y)
}
complex.substract = function(z1, z2){
return new complex(z1.x-z2.x, z1.y-z2.y)
}
complex.multiply = function(z1, z2){
return new complex(z1.x*z2.x - z1.y * z2.y, z1.x * z2.y+ z1.y * z2.x)
}
complex.zero = new complex(0, 0)
Mandelbrot分形
我建立了一個Mandelbrot Fractal(抽象資料型別表示)P(z) = z^2 + c,可在下面找到。
mandelbrot = function(c, z){return complex.add(complex.multiply(z, z), c)}
為了能夠繪製複數,我建立了一個complexPlane類。以下是JavaScript中的實現。
/*
* Plane
*
*/
complexPlane = function(width, height, real_min, real_max,
imaginary_min, imaginary_max, boundary, fractalIterationsPerPixel, canvasId) {
/**
* Plane width in pixels
*
*/
this.width = width
/**
* Plane height in pixels
*
*/
this.height = height
/**
* Real axis minimum value
*
*/
this.real_min = real_min
/**
* Real axis maximum value
*
*/
this.real_max = real_max
/**
* Imaginary axis minimum value
*
*/
this.imaginary_min = imaginary_min
/**
* Imaginary axis maximum value
*
*/
this.imaginary_max = imaginary_max
/**
* Boudary
*
*/
this.boundary = boundary
/**
* Number of Zn iterations per pixel
*
*/
this.fractalIterationsPerPixel = fractalIterationsPerPixel
/**
* Canvas Identifier
*
*/
this.canvasId = canvasId
/*
* Draws a fractal
*
*/
this.draw = function (fractal){
var canvas = document.getElementById(this.canvasId)
canvas.width = this.width
canvas.height = this.height
var context = canvas.getContext('2d')
context.fillStyle = 'yellow'
for(var x = 0; x < this.width; x++){
var xp = this.real_min + x * (this.real_max - this.real_min) / this.width
for(var y = 0; y < this.height; y++) {
var yp = this.imaginary_max - y *
(this.imaginary_max - this.imaginary_min) / this.height
var c = new complex(xp, yp)
var z = complex.zero
for(var k=0; k< this.fractalIterationsPerPixel;k++) z = fractal(c, z)
if(z.abs() < this.boundary) context.fillRect(x, y, 1, 1)
}
}
}
/*
* Displays 'Please wait...' at the center of the canvas
*
*/
this.pleaseWait = function(){
var canvas = document.getElementById(this.canvasId)
canvas.width = this.width
canvas.height = this.height
var context = canvas.getContext('2d')
context.fillStyle = 'yellow'
context.fillText('Please wait...', this.width/2 - 30, this.height/2)
}
}
因此,執行以下程式碼:
complexPlane = new complexPlane(300, 300, -1.5, 1.5, -1.5, 1.5, 1.5, 20, 'fractal')
mandelbrot = function(c, z){return complex.add(complex.multiply(z, z), c)}
complexPlane.pleaseWait()
setTimeout(function(){ complexPlane.draw(mandelbrot) }, 500)
這裡fractal是id帆布:
<canvas id="fractal">Your browser does not support HTML5 canvas.</canvas>
給出以下結果:
相關推薦
通過代數,數字,歐幾里得平面和分形討論JavaScript中的函數語言程式設計
本文是對函數語言程式設計正規化的系列文章從而拉開了與以下延續一個。 介紹 在JavaScript中,函式只是物件。因此,可以建構函式,作為引數傳遞,從函式返回或分配給變數。因此,JavaScript具有一流的功能。更準確地說,JavaScript支援以下內容: 高階函式引數 產生高階函式 巢狀函式 匿名
歐幾里得演算法和擴充套件歐幾里得演算法的簡單例子
歐幾里得演算法: #include <cstdio> #include <cstdlib> /* * 挑戰。。。p113 */ struct point{ //格點
LG 的數學計劃 ---- 第三步 歐幾里得演算法和擴充套件歐幾里得
於是,我們在完成神奇的前兩步之後,來到了這個神奇的地方——歐幾里得演算法和擴充套件歐幾里得演算法。 那麼,這是用來幹什麼的演算法呢? 算最大公約數(GCD)~~~ 好吧,考慮到有一些同學可能還不知道這是怎樣一種神奇的東西,那麼我就把這個東西的定義放到下面來
JavaScript ES6函數語言程式設計(二):柯里化、偏應用、組合、管道
上一篇介紹了閉包和高階函式,這是函數語言程式設計的基礎核心。這一篇來看看高階函式的實戰場景。 首先強調兩點: 注意閉包的生成位置,清楚作用域鏈,知道閉包生成後快取了哪些變數 高階函式思想:以變數作用域作為根基,以閉包為工具來實現各種功能 柯里化(curry) 定義:柯里化是把一個多引數函式轉換為一個巢狀的
演算法複習——擴充套件歐幾里得演算法(擴充套件歐幾里得,逆元,整除)
①歐幾里得演算法 就是求gcd的有趣的輾轉相除法,不再贅述啦0v0 程式碼: int gcd(int a,int b) { if(b==0) return a; else return gcd(b,a%b); } ②擴充套件歐幾里得演算法 需要解決這樣的問題:兩個非0整數a,b
數論-模運算,歐幾里得,擴充套件歐幾里得
一:模運算 1:餘數:a對b取模的結果就是a除以b的餘數,記作a%b。例如24%5 == 4 2:性質: \[ (a+b)\%p=(a\%p+b\%p)\%p \] \[ (a-b)\%p=(a\%p-b\%p+p)\%p \] \[ (a*b)\%p=(a\%p)*(b\%p)\%p \] 二:
ZOJ ~ 3609 ~ Modular Inverse (擴充套件歐幾里得,乘法逆元)
題意 求a*x ≡ 1(mod m),求最小的正整數 x ,如果沒有解輸出 “Not Exist”。 思路 求乘法逆元。a*x ≡ 1(mod m)轉化為 ,求最小的正!整數 x 。 #
ZOJ ~ 3593 ~ One Person Game (擴充套件歐幾里得,不定方程)
題意 你要從A走到B,你每次可以走a步,b步,a+b步問最小需要走多少步?無法到達輸出 -1。 題解 先不考慮a+b步的情況,那麼我們要求解的就是:,如果,證明無解。 假設原方程一組解為x0,y0,那麼通解(x,y)為:,。 其實也就是兩條直線:, 取一條平行於
逆元的幾種求法(擴充套件歐幾里得,費馬小定理或尤拉定理,特例,打表等)
乘法逆元 對於縮系中的元素,每個數a均有唯一的與之對應的乘法逆元x,使得ax≡1(mod n) 一個數有逆元的充分必要條件是gcd(a,n)=1,此時逆元唯一存在 逆元的含義:模n意義下,1個數a
除法取模逆元,擴充套件歐幾里得,費馬小定理[數學]
一、除法取模逆元 在演算法設計中,常會遇到求 a/b mod m的計算,當a很大,或者b很大,使得a/b的值無法直接計算的時候,通常採用逆元的方法,化除法為乘法。(逆元的概念在離散數學中 有學習) a
擴充套件歐幾里得,線性同餘方程 poj1845
定理:對於任意整數a,b存在一堆整數x,y,滿足ax+by=gcd(a,b) int exgcd(int a,int b,int &x,int &y){ if(b==0){x=1,y=0;return a;} int d=exgcd(b,a%b,x,y)
擴充套件歐幾里得演算法,解模線性方程,解ax+by=c的解集
typedef long long LL; LL exgcd(LL a,LL b,LL &x,LL &y){ if(a==0&&b==0) return -1
歐幾里得演算法(輾轉相除法)描述,證明和python實現
greatest common divisor 又稱輾轉相除法 演算法描述:給定兩個正整數m和n,求他們的最大公因子,即能夠同時整除m和n的最大正整數。 演算法步驟: 若m<n,那麼m↔n,為了確保m>n。 求m除以n得到的餘數r。 若r為0,演算法
歐幾里得演算法,也稱輾轉相除法,求公約數
#include <stdio.h> #include <stdlib.h> int main() { int a,b,r; printf("輸入兩個整數a,b:"); scanf("%d%d",&a,&
一點初等數論(擴充套件歐幾里得,求逆元的三種方法)
以前遇到數論題直接懵逼,今天開始好好搞搞基礎的數論知識。 一下內容證明我可能會省略,畢竟我太弱了…. . . . . . 1.模運算 幾個常用的定律: ( a + b ) mod p = ( a mod p + b mod p ) mod
CFF 1028 判斷互質(求最大公約數),歐幾里得演算法,輾轉相除法
題目: 輸入兩個正整數m和n,判斷m和n是否互質(即最大公約數為1),是則輸出Yes,否則輸出No。 輸入輸出: 輸入兩個整數m和n,中間用空格隔開。 如互質輸出Yes,否則輸出No。 樣例: 36 56 No 7 9 Yes 資
python常用演算法(6)——貪心演算法,歐幾里得演算法
1,貪心演算法 貪心演算法(又稱貪婪演算法)是指,在對問題求解時,總是做出在當前看來是最好的選擇。也就是說,不從整體最優上加以考慮,他所做出的的時在某種意義上的區域性最優解。 貪心演算法並不保證會得到最優解,但是在某些問題上貪心演算法的解就是最優解。要會判斷一個問題能否用貪心演算法來計算。貪心演算法和
歐幾裏得,擴展歐幾裏得(模板)
blank space string ref 返回 color quest ostream include 1 int gcd(int a,int b) 2 { 3 return b?gcd(b,a%b):a;//最後返回的a為最大公約數 4 } 擴展
bzoj 1938 - 類歐幾里得+線段樹
題目連結:https://darkbzoj.cf/problem/1938 解題思路; 對於區間更新: 前半部分可以用線段樹求等差數列和,後半部分可以用類歐幾里得演算法求出值 類歐幾里得 然後是要對區間離散化,其中有個問題在於對於區間(l,r)分裂為(
歐幾里得+擴充套件歐幾里得
歐幾里得演算法 歐幾里德演算法又稱輾轉相除法,用於計算兩個正整數a,b的最大公約數(gcd)。 其計算原理依賴於下面的定理: 定理:gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不為0) 證明:a可以表示成a = kb + r,則r = a