通俗地說決策樹演算法(二)例項解析
前情提要:
通俗地說決策樹演算法(一)基礎概念介紹
一. 概述
上一節,我們介紹了決策樹的一些基本概念,包括樹的基本知識以及資訊熵的相關內容,那麼這次,我們就通過一個例子,來具體展示決策樹的工作原理,以及資訊熵在其中承擔的角色。
有一點得先說一下,決策樹在優化過程中,有3個經典的演算法,分別是ID3,C4.5,和CART。後面的演算法都是基於前面演算法的一些不足進行改進的,我們這次就先講ID3演算法,後面會再說說它的不足與改進。
二. 一個例子
眾所周知,早上要不要賴床是一個很深刻的問題。它取決於多個變數,下面就讓我們看看小明的賴床習慣吧。
| 季節 | 時間已過 8 點 | 風力情況 | 要不要賴床 |
|---|---|---|---|
| spring | no | breeze | yes |
| winter | no | no wind | yes |
| autumn | yes | breeze | yes |
| winter | no | no wind | yes |
| summer | no | breeze | yes |
| winter | yes | breeze | yes |
| winter | no | gale | yes |
| winter | no | no wind | yes |
| spring | yes | no wind | no |
| summer | yes | gale | no |
| summer | no | gale | no |
| autumn | yes | breeze | no |
OK,我們隨機抽了一年中14天小明的賴床情況。現在我們可以根據這些資料來構建一顆決策樹。
可以發現,資料中有三個屬性會影響到最終的結果,分別是,季節,時間是否過8點,風力情況。
要構建一顆決策樹,首先我們要找到它的根,按照上一節所說,我們需要計算每一個屬性的資訊熵。
在計算每一個屬性的資訊熵之前,我們需要先根據歷史資料,計算沒有任何屬性影響下的賴床資訊熵。從資料我們可以知道,14天中,有賴床為8天,不賴床為6天。則
p(賴床) = 8 / 12.
p(不賴床) = 6 / 12.資訊熵為
H(賴床) = -(p(賴床) * log(p(賴床)) + p(不賴床) * log(p(不賴床))) = 0.89接下來就可以來計算每個屬性的資訊熵了,這裡有三個屬性,即季節,是否過早上8點,風力情況,我們需要計算三個屬性的每個屬性在不同情況下,賴床和不賴床的概率,以及熵值。
說得有點繞,我們先以風力情況這一屬性來計算它的資訊熵是多少,風力情況有三種,我們分別計算三種情況下的熵值。
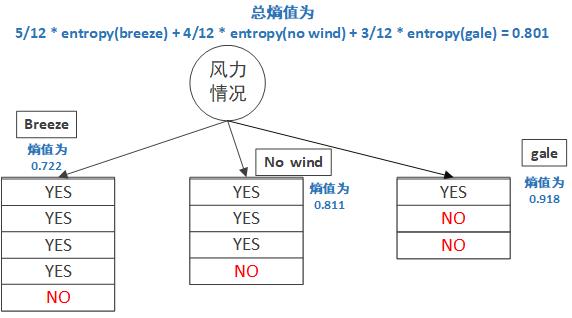
風力情況為 breeze 時,有 4 / 5 的概率會賴床,而 1 / 5 的概率不會賴床,它的熵為 entropy(breeze) = -(p(breeze,賴床) * log(p(breeze,賴床)) + p(breeze,不賴床) * log(p(breeze,不賴床))) 0.722。
風力情況為 no wind 時,和上面一樣的計算,熵值為 entropy(no wind) = 0.811
風力情況為 gale 時,熵值為 entropy(gale) = 0.918最終,風力情況這一屬性的熵值為其對應各個值的熵值乘以這些值對應頻率。
H(風力情況) = 5/12 * entropy(breeze) + 4/12 * entropy(no wind) + 3/12 * entropy(gale) = 0.801還記得嗎,一開始什麼屬性沒有,賴床的熵是H(賴床)=0.89。現在加入風力情況這一屬性後,賴床的熵下降到了0.801。這說明資訊變得更加清晰,我們的分類效果越來越好。
以同樣的計算方式,我們可以求出另外兩個屬性的資訊熵:
H(季節) = 0.56
H(是否過 8 點) = 0.748通過它們的資訊熵,我們可以計算出每個屬性的資訊增益。沒錯,這裡又出現一個新名詞,資訊增益。不過它不難理解,資訊增益就是拿上一步的資訊熵(這裡就是最原始賴床情況的資訊熵)減去選定屬性的資訊熵,即
資訊增益 g(季節) = H(賴床) - H(季節) = 0.33
這樣我們就能計算每個屬性的資訊增益,然後選取資訊增益最大的那個作為根節點就行了,在這個例子中,很明顯,資訊增益最大的是季節這個屬性。
選完根節點怎麼辦?把每個節點當作一顆新的樹,挑選剩下的屬性,重複上面的步驟就可以啦。
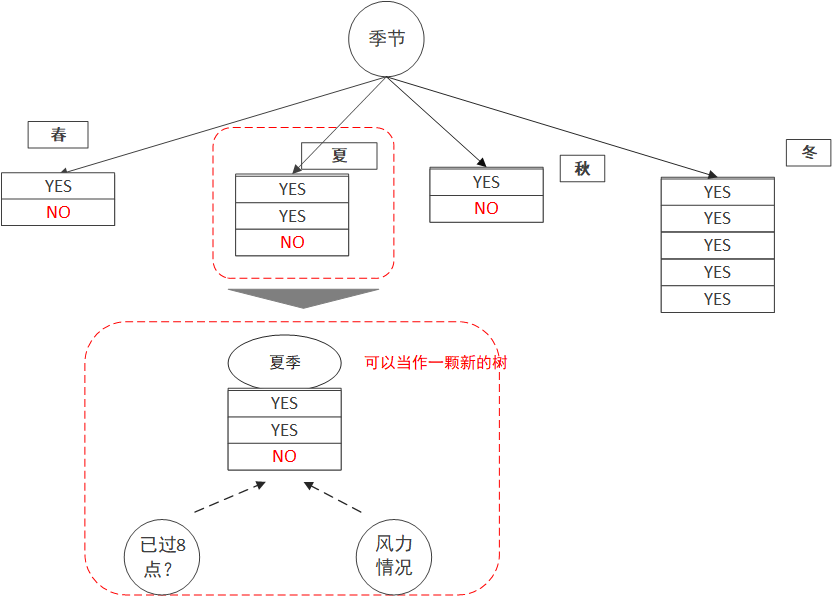
當全部都遍歷完之後,一顆完整的樹也就構建出來了,這個例子中,我們最終構造的樹會是這個樣子的:
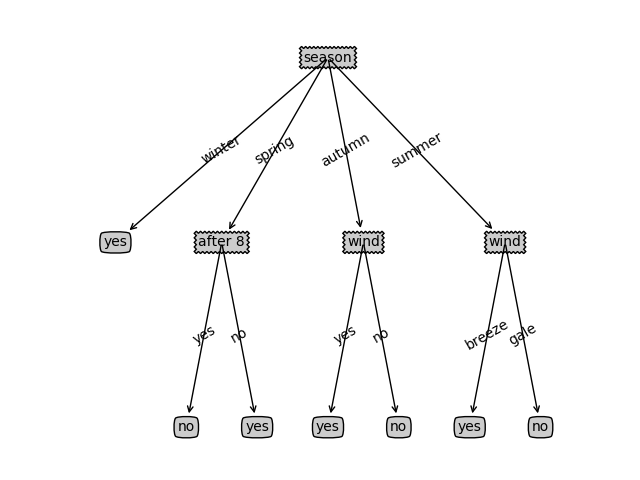
三. 過擬合與剪枝
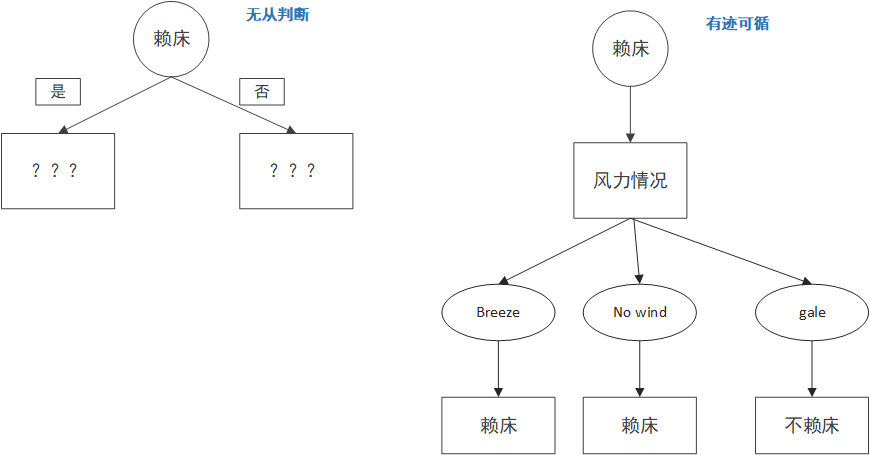
在構建決策樹的時候,我們的期望是構建一顆最矮的決策樹,為什麼需要構建最矮呢?這是因為我們要避免過擬合的情況。
什麼是過擬合呢,下圖是一個分類問題的小例子,左邊是正常的分類結果,右邊是過擬合的分類結果。
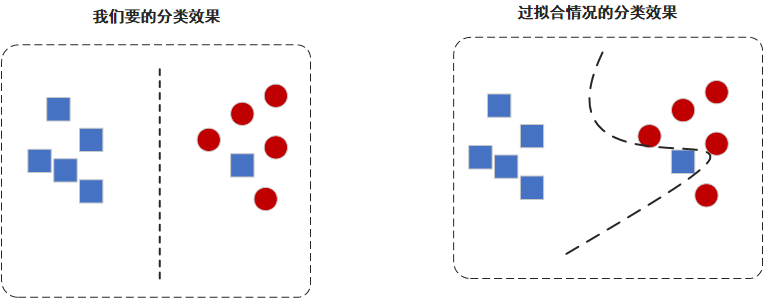
在現實世界中,我們的資料通常不會很完美,資料集裡面可能會有一些錯誤的資料,或是一些比較奇葩的資料。如上圖中的藍色方塊,正常情況下我們是允許一定的誤差,追求的是普適性,就是要適應大多數情況。但過擬合的時候,會過度追求正確性,導致普適性很差。
剪枝,即減少樹的高度就是為了解決過擬合,你想想看,過擬合的情況下,決策樹是能夠對給定樣本中的每一個屬性有一個精準的分類的,但太過精準就會導致上面圖中的那種情況,喪失了普適性。
而剪枝又分兩種方法,預剪枝幹,和後剪枝。這兩種方法其實還是蠻好理解的,一種是自頂向下,一種是自底向上。我們分別來看看。
預剪枝
預剪枝其實你可以想象成是一種自頂向下的方法。在構建過程中,我們會設定一個高度,當達構建的樹達到那個高度的時候呢,我們就停止建立決策樹,這就是預剪枝的基本原理。
後剪枝
後剪枝呢,其實就是一種自底向上的方法。它會先任由決策樹構建完成,構建完成後呢,就會從底部開始,判斷哪些枝幹是應該剪掉的。
注意到預剪枝和後剪枝的最大區別沒有,預剪枝是提前停止,而後剪枝是讓決策樹構建完成的,所以從效能上說,預剪枝是會更塊一些,後剪枝呢則可以更加精確。
ID3決策樹演算法的不足與改進
ID3決策樹不足
用ID3演算法來構建決策樹固然比較簡單,但這個演算法卻有一個問題,ID3構建的決策樹會偏袒取值較多的屬性。為什麼會有這種現象呢?還是舉上面的例子,假如我們加入了一個屬性,日期。一年有365天,如果我們真的以這個屬性作為劃分依據的話,那麼每一天會不會賴床的結果就會很清晰,因為每一天的樣本很少,會顯得一目瞭然。這樣一來資訊增益會很大,但會出現上面說的過擬合情況,你覺得這種情況可以泛化到其他情況嗎?顯然是不行的!
C4.5決策樹
針對ID3決策樹的這個問題,提出了另一種演算法C4.5構建決策樹。
C4.5決策樹中引入了一個新的概念,之前不是用資訊增益來選哪個屬性來作為枝幹嘛,現在我們用增益率來選!

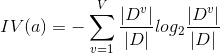
這裡面,IV(a)這個,當屬性可選的值越多(比如一年可取365個日期)的時候,它的值越大。
而IV(a)值越大,增益率顯然更小,這就出現新問題了。C4.5決策樹跟ID3決策樹反過來,它更偏袒屬性可選值少的屬性。這就很麻煩了,那麼有沒有一種更加公正客觀的決策樹演算法呢?有的!!
CART 決策樹
上面說到,ID3決策樹用資訊增益作為屬性選取,C4.5用增益率作為屬性選取。但它們都有各自的缺陷,所以最終提出了CART,目前sklearn中用到的決策樹演算法也是CART。CART決策樹用的是另一個東西作為屬性選取的標準,那就是基尼係數。
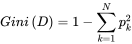
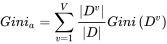
第一條公式中pk表示的是每個屬性的可選值,將這些可選值計算後累加。這條公式和資訊增益的結果其實是類似的,當屬性分佈越平均,也就是資訊越模糊的時候,基尼係數值會更大,反之則更小。但這種計算方法,每次都只用二分分類的方式進行計算。比如說上面例子中的季節屬性,有春夏秋冬四個可選值(春,夏,秋,冬)。那麼計算春季的時候就會按二分的方式計算(春,(夏,秋,冬))。而後面其他步驟與ID3類似。通過這種計算,可以較好得規避ID3決策樹的缺陷。
所以如果用CART演算法訓練出來的決策樹,會和我們上面ID3訓練出來的決策樹有些不一樣。在下一篇文章就會用sklearn來使用CART演算法訓練一顆決策樹,並且會將結果通過畫圖的方式展現。
推薦閱讀:
Scala 函數語言程式設計指南(一) 函式式思想介紹
Actor併發程式設計模型淺析
大資料儲存的進化史 --從 RAID 到 Hadoop Hdfs
C,java,Python,這些名字背後的江湖
