0 引言

  決策樹是一種基本的分類和迴歸方法。決策樹模型呈樹形結構，在分類問題中，表示基於特徵對例項進行分類的過程。可以認為是if-then規則的集合，也可以認定是定義在特徵空間與類空間上的條件概率分佈。其主要特點是模型具有可讀性，分類速度快。學習時，利用訓練資料，根據損失函式最小化的原則建立決策樹模型。預測時，對新的資料，利用決策樹模型進行分類。決策樹學習通常包括3個步驟：特徵選取、決策樹的生成和決策樹的修剪。

1 決策樹模型與學習

1.1 決策樹模型

  定義1：分類決策樹模型是一種描述對例項進行分類的樹形結構。決策樹有結點和有向邊組成。結點有兩種型別：內部結點和葉結點。內部結點表示一個特徵或屬性，葉結點表示一個類。
  用決策樹分類，從根結點開始，對例項的某一特徵進行測試，根據測試結果，將例項分配到其子結點；這時，每一個子結點對應著該特徵的一個取值，如此遞迴地對例項進行測試分配，直至達到葉結點。最後將例項分到葉結點的類中。
  圖1展示了一個決策樹的示意圖，圖中圓和方框分別表示內部結點和葉結點。
  

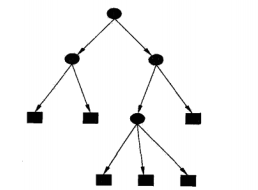
圖1 決策樹模型

1.2 決策樹與if-then規則

  可以將決策樹看成一個if-then規則的集合，見決策樹轉換為if-then規則的過程是這樣的：有決策樹的根結點到葉結點的每一天路徑構建一條規則；路徑上內部結點的特徵對應著規則的條件，而葉結點的類對應著規則的結論。決策樹的路徑或去對應的if-then規則集合有一個重要的性質：互斥並且完備。這就是說，每一個例項都被一條路徑或一條規則所覆蓋，而且只被一條路徑或一條規則所覆蓋。這裡的覆蓋是指例項的特徵與路徑上的特徵一致或例項滿足規則的條件。

1.3 決策樹與條件概率分佈

  決策樹還表示給定特徵條件下類的概率分佈，這一條件概率分佈定義在特徵區間的一個劃分上。將特徵區間劃分為互不相交的單元或區域，並在每個單元定義的一個類的概率分佈就構成了一個條件概率分佈。決策樹的一條路徑對應於劃分中的一個單元。決策樹所表示的條件概率分佈由各個單元給定條件下類的條件概率分佈組成。假設$X$

X為表示特徵的隨機變數，$Y$表示類的隨機變數，那麼這個條件概率分佈可以表示為$P(Y|X)$。$X$取值與給定劃分下單元的集合，$Y$取值於類的集合。各葉結點（單元）上的條件概率往往偏向於某一類，即屬於某一類的概率較大。決策樹分類時將該結點的例項強行分到條件概率大的那一類去。

1.4 決策樹學習

  決策樹學習，假設給定訓練資料集
$D=\{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\}$
其中，$x_i=(x_i^{\left(1\right)},x_i^{}$

(2),…,xi(n))Tx_i=(x_i^{(1)},x_i^{(2)},\dots,x_i^{(n)})^T為輸入例項（特徵向量），$n$為特徵個數，$y_i\in\{1,2,\dots,K\}$為類標記，$i=1,2,\dots,N$，$N$為樣本容量。學習的目標是根據訓練資料集構建一個決策樹模型，使它能夠對例項進行正確的分類。
  決策樹學習本質上是從訓練資料集中歸納出一組分類規則，與訓練資料集不相矛盾的決策樹（即能對訓練資料進行正確分類的決策樹）可能有多個，也可能一個都沒有。我們需要的是一個與訓練資料矛盾較小的決策樹，同時具有很好的泛化能力。從另一個角度看，決策樹學習是由訓練資料集估計條件概率模型。基於特徵空間劃分的類的條件概率模型有無窮多個。我們選擇的條件概率模型應該不僅對訓練資料有很好的擬合，而且對未知資料有很好的預測。
  決策樹學習用損失函式表示這一目標。如下所述，決策樹學習的損失函式通常是正則化的極大似然函式。決策樹學習的策略是以損失函式為目標函式的最小化。當損失函式確定以後，學習問題就變成為在損失函式意義下選擇最優決策樹的問題。因為從所有可能的決策樹中選取最優決策樹中選取最優決策樹是NP完全問題，所以現實中決策樹學習演算法通常採用啟發式方法，近似求解這一最優化問題。這樣得到的決策樹是次最優的。
  決策樹學習的演算法通常是一個遞迴地選擇最優特徵，並根據該特徵對訓練資料進行分割，使得對各個子資料集有一個最好的分類的過程。這一過程對應著特徵空間的劃分，也對應著決策樹的構建。開始，構建根結點，將所有訓練資料都放在根結點。選擇一個最優特徵，按照這一特徵將訓練資料集分割成子集，使得各個子集有一個在當前條件下最好的分類。如果這些子集已經能夠被基本正確分類，那麼構建葉結點，並將這些子集分到所對應的葉結點中去；如果還有子集不能被基本正確分類，那麼就對這些子集選擇新的最優特徵，繼續對其進行分割，構建相應的結點，如此遞迴地進行下去，直至所有訓練資料子集被基本正確分類，或者沒有合適的特徵為止。最後每個子集都被分到葉結點上，即都有了明確的類，這就生成了一顆決策樹。
  以上方法生成的決策樹可能對訓練資料有很好的分類能力，但對未知的測試資料卻未必有很好的分類能力，即可能發生過擬合現象。我們需要對已生成的樹自下而上進行剪枝，將樹變得簡單，從而使它有很好的泛化能力。具體地，就是去掉過於細分的葉結點，使其回退到父節點，甚至更高的結點，然後將父節點或者更高的結點改為新的葉結點。
  如果特徵數量很多，也可以在決策樹學習開始的時候，對特徵進行選擇，只留下對訓練資料有足夠分類能力的特徵。
  可以看出，決策樹學習演算法包含特徵選擇、決策樹的生成與決策樹的剪枝過程。由於決策樹表示一個條件概率分佈，所以深淺不同的決策樹對應著不同複雜度的概率模型，決策樹的生成對應於模型的區域性選擇，決策樹的剪枝對應於模型的全域性選擇，決策樹的生成只考慮區域性最優，相對地，決策樹的剪枝則會考慮全域性最優。決策樹學習的常用演算法有ID3，C4.5與CART演算法。

2 特徵選取

  特徵選擇在於選取對訓練資料具有分類能力的特徵。這樣可以提高決策樹學習效率。如果利用一個特徵進行分類的結果與隨機分類的結果沒有很大差別，則稱這個特徵時沒有分類能力的。經驗上扔掉這樣的特徵對決策樹學習的精度影響不大。通常特徵選擇的準則是資訊增益或者資訊增益比。

2.1 資訊增益

  先來介紹一下資訊理論中熵和條件熵的概念。
  熵（entropy）是用來表示隨機變數不確定性的度量。設$X$是一個取有限個值的離散隨機變數，其概率分佈為
$P(X=x_i)=p_i，i=1,2,\dots,n$
則隨機變數$X$的熵定義為
$H(X)=-\sum_{i=1}^n {p_i\log{p_i}} \tag1$
在式(1)中，若$p_i=0$，則定義$0\log0=0$。通常，式(1）中的對數以2為底或以e為底（自然對數），這是熵的單位分別稱作位元（bit）或納特（nat）。由定義可知，熵只依賴於$X$的分佈，而與$X$的取值無關，所以也可以將$X$的熵記作$H(p)$，即
$H(p)=-\sum_{i=1}^n {p_i}\log{p_i}\tag2$
  熵越大，隨機變數的不確定性就越大。從定義可驗證
$0\leq H(p)\leq \log n\tag3$
  當隨機變數只取兩個值，例如1,0時，即X的分佈為
$P(X=1)=p, P(X=0)=1-p, 0\leq p \leq 1$
熵為
$H(p)=-p \log_2{p}-(1-p)\log_2(1-p)\tag4$
這時，熵$H(p)$隨概率$p$的變化曲線如下圖所示（單位為位元）：
  

圖2 分佈為貝努力分佈時熵與概率的關係
  當$p=0$或者$p=1$時，$H(p)$為0，隨機變數完全沒有不確定性，當$p=0.5$時，$H(p)=1$，熵取值最大，隨機變數不確定性最大。
  設有隨機變數$(X,Y)$，其聯合概率分佈為
$P(X=x_i,Y=y_j)=p_{ij}, i=1,2,\dots,n;j=1,2,\dots,m$
條件熵$H(Y|X)$表示在已知隨機變數$X$的條件下隨機變數$Y$的不確定性。隨機變數$X$給定的條件下隨機變數$Y$的條件熵$H(Y|X)$，定義為$X$給定條件下Y的條件概率分佈的熵對$X$的數學期望
$H(Y|X)=\sum_i^np_iH(Y|X=x_i)\tag5$
這裡，$p_i=P(X=x_i),i=1,2,\dots,n.$
  當熵和條件熵中的概率由資料估計（特別是極大似然估計）得到時，所對應的熵與條件熵分別稱為經驗熵和經驗條件熵。此時，如果有0概率，令$0\log0=0$。
資訊增益表示得知特徵$X$的資訊而使得類$Y$的資訊的不確定性減少的程度。
  定義2（資訊增益） 特徵A對訓練資料集D的資訊增益g(D,A)，定義為集合D的經驗熵H(D)與特徵A給定條件下D的經驗條件熵H(D|A)之差，即
$g(D,A)=H(D)-H(D|A)\tag6$
  一般地，熵H(Y)與H(Y|X)之差稱為互資訊，決策樹學習中的資訊增益等價於訓練資料集中類與特徵的互資訊。
  根據資訊增益準則的特徵選擇方法是：對訓練資料集（或子集）D，計算其每個特徵的資訊增益，並比較它們的大小，選擇資訊增益最大的特徵。
  設訓練資料集為$D$，$|D|$表示其樣本容量，即樣本個數。設有$K$個類$C_k，k=1,2,\dots,K，|C_k|$的樣本個數，$\sum_{k=1}^K |C_k|=|D|$。設特徵$A$有n個不同的取值$\{a_1,a_2,\dots,a_n\}$