2019.9.17 初級資料結構——並查集及其應用
一、並查集基礎
(一)引入
我們先來看一個問題。
某學校有N個學生,形成M個俱樂部。每個俱樂部裡的學生有著一定相似的興趣愛好,形成一個朋友圈。一個學生可以同時屬於若干個不同的俱樂部。根據“我的朋友的朋友也是我的朋友”這個推論可以得出,如果A和B是朋友,且B和C是朋友,則A和C也是朋友。請編寫程式計算最大朋友圈中有多少人。
輸入格式:
輸入的第一行包含兩個正整數N(≤30000)和M(≤1000),分別代表學校的學生總數和俱樂部的個數。後面的M行每行按以下格式給出1個俱樂部的資訊,其中學生從1~N編號:
第i個俱樂部的人數Mi(空格)學生1(空格)學生2 … 學生Mi
輸出格式:
輸出給出一個整數,表示在最大朋友圈中有多少人。
輸入樣例:
7 4
3 1 2 3
2 1 4
3 5 6 7
1 6
輸出樣例:
4
我們把這個題抽象化:
現在有n個數,它們按照一定規律合併,形成一些集合,求最大集合的元素個數。
這個合併規律如下:
(1)同一個俱樂部的所有人屬於同一個集合;
(2)若兩個俱樂部包含同一個人,則這兩個俱樂部屬於同一個集合。
按照正常做法,我們對於每一個人按照上述規律掃描剩餘的人,運行復雜度O(n^很大)。
這個方法顯然過不了。
我們重新分析這個題目,主要難點有兩個:
第一,對於第一條,同一個俱樂部的所有人如何儲存它們所在同一個集合內。
這個很好解決,我們再開一個book陣列,對於每一個人i,假設它在cnt集合內,我們標記book[i]=cnt。
如果這樣標記,對於第二個合併規律,我們掃描另一個俱樂部的所有人,我們把每一個book[i]都置成要合併到的俱樂部,總複雜度O(nm)。
但這樣還是過不了,所以我們考慮把第二個合併步驟的複雜度優化到O(1),也就是說我們只需要修改一個數就可以修改整個集合。
對於這樣的修改方式,我們可以想到一種資料結構——樹。
利用樹儲存每個集合有兩個好處:
第一,每棵樹只有一個樹根(也就是查詢樹根就可以查詢整棵樹)
第二,兩棵樹合併只需要把一棵樹的樹根接到另一棵上(所以修改的複雜度是O(1))。
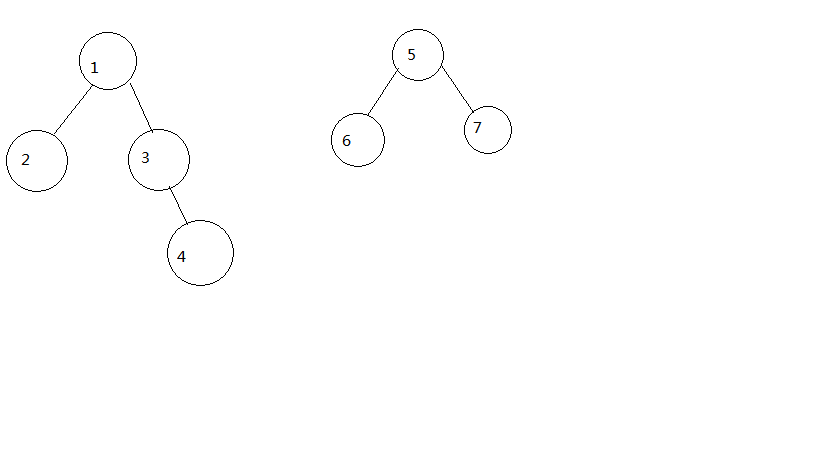
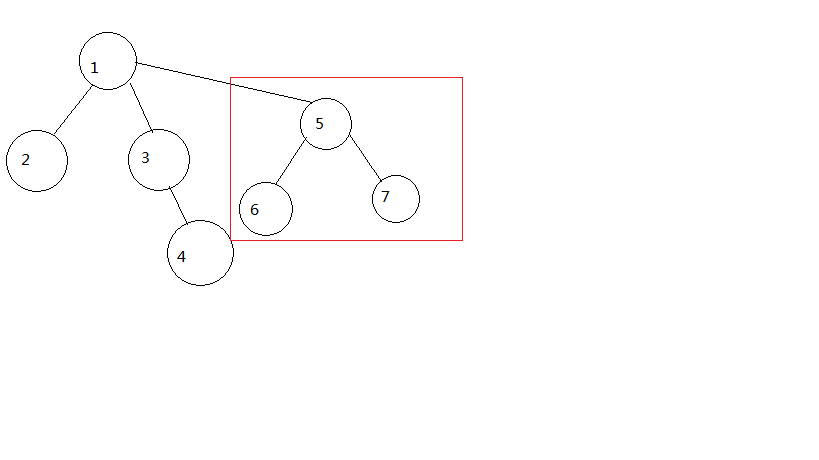
大概就是上面這麼合併
也就是說我們可以用樹優化查詢和合並集合的過程,其本質就是對樹之間的處理。
又因為,這一類題的根本步驟就是查詢與合併,所以我們把這樣的資料結構叫做並查集。
(二)並查集的基本操作
剛才我們已經知道,並查集中合併兩個元素實際上是合併他們所在樹的祖先。
為了查詢這兩個點是否在一棵樹上,我們首先要找到他們兩個點的祖先分別是誰,並判斷他們的祖先是否是同一個點即可。
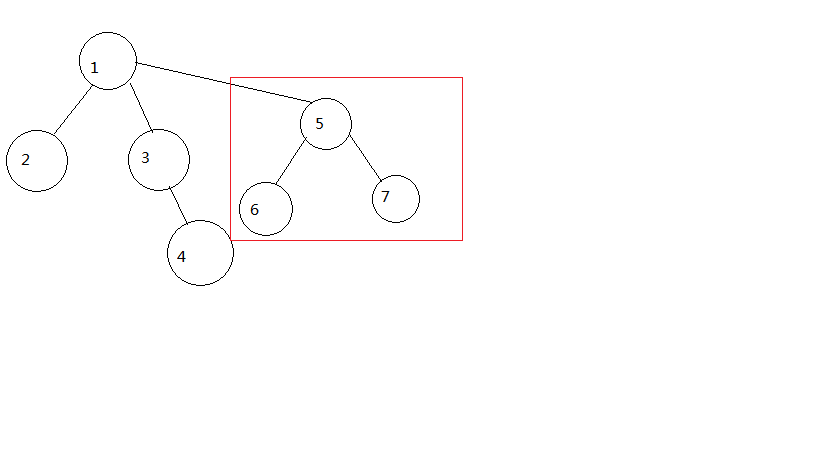
但是因為樹會退化成一條鏈,所以我們在查詢祖先時要把下圖的第一個樹變成第二個樹,這是後話。


第二個圖的意思就是所有的點都連到根節點上。
我們暫且不提怎麼查詢一個點的祖先,在我們查詢兩個點祖先之後,判斷他們的祖先是不是同一個點,如果不是同一個點合併即可。
所以我們用fa[x]表示x的父親,則程式碼如下:
void u(int a,int b)
{
int c=f(a),d=f(b);
if(fa[c]!=fa[d])
{
fa[min(c,d)]=fa[max(c,d)];
return;
}
}
一定要注意的是,絕對不能讓fa[min(a,b]直接等於fa[max(a,b)],因為這樣只合並了兩個點,而不是其所在的樹。
同時,注意合併時要按照一定的大小順序,所以這裡是按小往大合的。
所以這是合併兩個點的方法。
關於查詢祖先的方法,有一個非常絕妙的方法:
int f(int o)
{
if(fa[o]==o)return o;
return fa[o]=f(fa[o]);
}
第一行非常容易理解,如果o的祖先時自己則它自己就是這棵樹的祖先。
第二行我們把它分解成兩部分:
(1)f(fa[o])找到fa[o]的祖先。
(2)return fa[o]=f(fa[o]) 將o的父親置為其父親的祖先
也就是說 我們成功把一棵近似於一條鏈的樹 弄成了一棵最多隻有三層的樹。
這個過程換句話說是這樣:
(1)遞迴地找點o每一級祖先o',直到找到它真正的祖先o1;
(2)回溯,對於每一個o',將fa[o]置為o1.
也就是說 通過這個步驟,這棵樹的每一個點都直接連線到了祖先上
所以回到這章開始的部分,對於那兩棵樹之間的變化,有一種方法就是上面說的更改每個點與祖先的連線方式,這種方式叫作路徑壓縮。
其實還有一個稍微好實現一點的方法,對於每個樹根,我們記錄它所在的樹的高度,把這個高度叫作這棵樹的秩。
對於每個合併操作(不是路徑壓縮時的查詢操作),我們把秩小的樹合到秩大的樹上,這樣可以保證合出來的新樹的秩不大於原來任何一棵樹。
若兩棵樹的秩一樣,則新樹的秩是原樹的秩+1.
這種方法也叫按秩合併。
最後記得一開始初始化,令fa[x]=x。
上個板子:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int fa[100050];
int f(int o)
{
if(fa[o]==o)return o;
return fa[o]=f(fa[o]);
}
void u(int a,int b)
{
int c=f(a),d=f(b);
if(c!=d)fa[min(c,d)]=fa[max(c,d)];
return;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++)
{
int x,y,opt;
scanf("%d%d%d",&x,&y,&opt);
if(!opt)u(x,y);
else
{
if(f(x)!=f(y))puts("NO");
else puts("YES");
}
}
return 0;
}
高階用法待填坑。
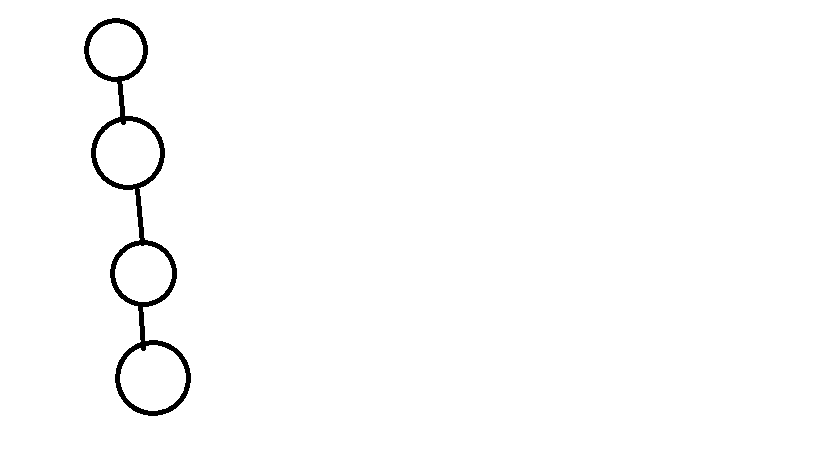

&n
