直觀理解為什麼分類問題用交叉熵損失而不用均方誤差損失?
目錄
- 交叉熵損失與均方誤差損失
- 損失函式角度
- softmax反向傳播角度
- 參考
部落格:blog.shinelee.me | 部落格園 | CSDN
交叉熵損失與均方誤差損失
常規分類網路最後的softmax層如下圖所示,傳統機器學習方法以此類比,
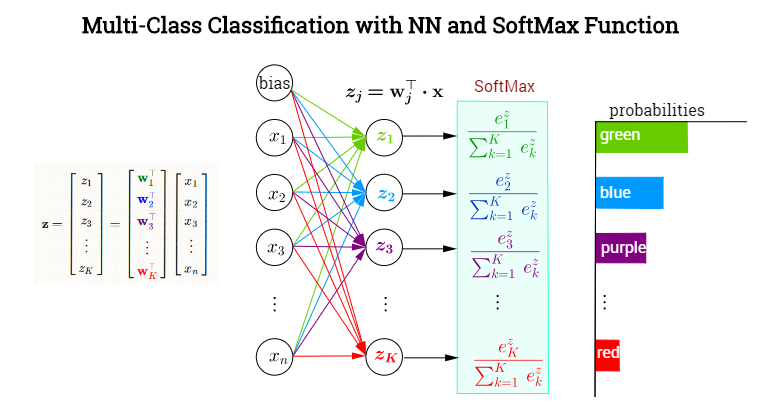
一共有\(K\)類,令網路的輸出為\([\hat{y}_1,\dots, \hat{y}_K]\),對應每個類別的概率,令label為 \([y_1, \dots, y_K]\)。對某個屬於\(p\)類的樣本,其label中\(y_p=1\),\(y_1, \dots, y_{p-1}, y_{p+1}, \dots, y_K\)均為0。
對這個樣本,交叉熵(cross entropy)損失為
\[
\begin{aligned}L &= - (y_1 \log \hat{y}_1 + \dots + y_K \log \hat{y}_K) \\&= -y_p \log \hat{y}_p \\ &= - \log \hat{y}_p\end{aligned}
\]
均方誤差損失(mean squared error,MSE)為
\[
\begin{aligned}L &= (y_1 - \hat{y}_1)^2 + \dots + (y_K - \hat{y}_K)^2 \\&= (1 - \hat{y}_p)^2 + (\hat{y}_1^2 + \dots + \hat{y}_{p-1}^2 + \hat{y}_{p+1}^2 + \dots + \hat{y}_K^2)\end{aligned}
\]
\[ \ell = \frac{1}{m} \sum_{i=1}^m L_i \]
對比交叉熵損失與均方誤差損失,只看單個樣本的損失即可,下面從兩個角度進行分析。
損失函式角度
損失函式是網路學習的指揮棒,它引導著網路學習的方向——能讓損失函式變小的引數就是好引數。
所以,損失函式的選擇和設計要能表達你希望模型具有的性質與傾向。
對比交叉熵和均方誤差損失,可以發現,兩者均在\(\hat{y} = y = 1\)時取得最小值0,但在實踐中\(\hat{y}_p\)只會趨近於1而不是恰好等於1,在\(\hat{y}_p < 1\)的情況下,
- 交叉熵只與label類別有關,\(\hat{y}_p\)越趨近於1越好
- 均方誤差不僅與\(\hat{y}_p\)有關,還與其他項有關,它希望\(\hat{y}_1, \dots, \hat{y}_{p-1}, \hat{y}_{p+1}, \dots, \hat{y}_K\)越平均越好,即在\(\frac{1-\hat{y}_p}{K-1}\)時取得最小值
分類問題中,對於類別之間的相關性,我們缺乏先驗。
雖然我們知道,與“狗”相比,“貓”和“老虎”之間的相似度更高,但是這種關係在樣本標記之初是難以量化的,所以label都是one hot。
在這個前提下,均方誤差損失可能會給出錯誤的指示,比如貓、老虎、狗的3分類問題,label為\([1, 0, 0]\),在均方誤差看來,預測為\([0.8, 0.1, 0.1]\)要比\([0.8, 0.15, 0.05]\)要好,即認為平均總比有傾向性要好,但這有悖我們的常識。
而對交叉熵損失,既然類別間複雜的相似度矩陣是難以量化的,索性只能關注樣本所屬的類別,只要\(\hat{y}_p\)越接近於1就好,這顯示是更合理的。
softmax反向傳播角度
softmax的作用是將\((-\infty, +\infty)\)的幾個實數對映到\((0,1)\)之間且之和為1,以獲得某種概率解釋。
令softmax函式的輸入為\(z\),輸出為\(\hat{y}\),對結點\(p\)有,
\[
\hat{y}_p = \frac{e^{z_p}}{\sum_{k=1}^K e^{z_k}}
\]
\(\hat{y}_p\)不僅與\(z_p\)有關,還與\(\{z_k | k\neq p\}\)有關,這裡僅看$z_p $,則有
\[
\frac{\partial \hat{y}_p}{\partial z_p} = \hat{y}_p(1-\hat{y}_p)
\]
\(\hat{y}_p\)為正確分類的概率,為0時表示分類完全錯誤,越接近於1表示越正確。根據鏈式法則,按理來講,對與\(z_p\)相連的權重,損失函式的偏導會含有\(\hat{y}_p(1-\hat{y}_p)\)這一因子項,\(\hat{y}_p = 0\)時分類錯誤,但偏導為0,權重不會更新,這顯然不對——分類越錯誤越需要對權重進行更新。
對交叉熵損失,
\[
\frac{\partial L}{\partial \hat{y}_p} = -\frac{1}{\hat{y}_p}
\]
則有
\[
\frac{\partial L}{\partial \hat{z}_p} = \frac{\partial L}{\partial \hat{y}_p} \cdot \frac{\partial \hat{y}_p}{\partial z_p} = \hat{y}_p - 1
\]
恰好將\(\hat{y}_p(1-\hat{y}_p)\)中的\(\hat{y}_p\)消掉,避免了上述情形的發生,且\(\hat{y}_p\)越接近於1,偏導越接近於0,即分類越正確越不需要更新權重,這與我們的期望相符。
而對均方誤差損失,
\[
\frac{\partial L}{\partial \hat{y}_p} = -2(1-\hat{y}_p)=2(\hat{y}_p - 1)
\]
則有,
\[
\frac{\partial L}{\partial \hat{z}_p} = \frac{\partial L}{\partial \hat{y}_p} \cdot \frac{\partial \hat{y}_p}{\partial z_p} = -2 \hat{y}_p (1 - \hat{y}_p)^2
\]
顯然,仍會發生上面所說的情況——\(\hat{y}_p = 0\),分類錯誤,但不更新權重。
綜上,對分類問題而言,無論從損失函式角度還是softmax反向傳播角度,交叉熵都比均方誤差要好。
參考
- Loss Functions
- Why You Should Use Cross-Entropy Error Instead Of Classification Error Or Mean Squared Error For Neural Network Classifier Training
