大家還好嗎？
背景就不用多說了吧？本來我是初四上班的，現在延長到2月10日了。這是我工作以來時間最長的一個假期了。可惜哪也去不了。待在家裡，沒啥事，就用python模擬預測一下新冠病毒肺炎的資料吧。要宣告的是本文純屬個人自娛自樂，不代表真實情況。
採用SIR模型，S代表易感者，I表示感染者，R表示恢復者。染病人群為傳染源，通過一定機率把傳染病傳給易感人群，ta自己也有一定的機率被治癒並免疫，或死亡。易感人群一旦感染即成為新的傳染源。
模型假設:
①不考慮人口出生、死亡、流動等情況，即人口數量保持常數。
②一個病人一旦與易感者接觸就必然具有一定的傳染力。假設 t 時刻單位時間內，一個病人能傳染的易感者數目與此環境內易感者總數s(t)成正比，比例係數為β，從而在t時刻單位時間內被所有病人傳染的人數為βs(t)i(t)。
③ t 時刻，單位時間內從染病者中移出的人數與病人數量成正比，比例係數為γ，單位時間內移出者的數量為γi(t)。
模型為

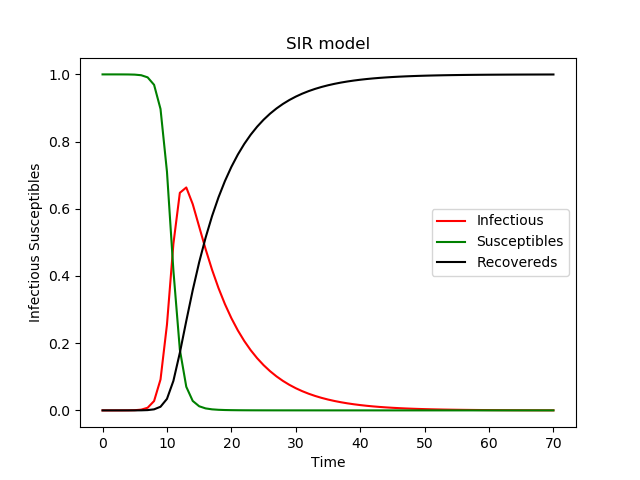
現在的問題就是利用現有的資料找到新冠肺炎的β值，γ值等資料了。先把資料拔下來吧。從[3]上扒資料，由於資料不多，就手工完成吧。儲存到csv檔案裡。
然後把資料作圖

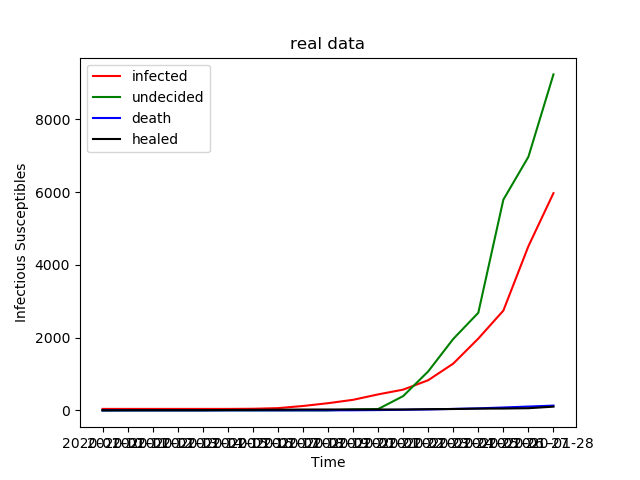
還有一個指標是再生數R0=β/γ，大於1時人群中大部分才被感染[4]。世衛組織1月23日的估計是R0在1.4到2.5之間[5]，最新的根據前425例發病資料的估計值為2.2[6]。
文章[7]中的按一般病毒性肺炎恢復期25天計算得到的γ值為0.04。
關於β值和初始易感人群，[7]的作者採用的方法是先估計一個區間，然後用最小二乘法找到最佳引數，β≈3.57*10^-5。S[0]的範圍為5000-30000人。[7]文章裡有matlab程式碼，我用python改寫一下，由於對最小二乘法法的實現比較陌生，嘗試了半天，最後我決定用最笨的辦法——窮舉法。就是用兩個巢狀迴圈將範圍內所有β值和S0值都試一遍，計算每次嘗試結果與實際資料之間差值的平方和，平方和最小的一組β值和S0值用來做預測。程式碼如下:
γ值設定為0.04，即一般病程25天
用最小二乘法估計β值和初始易感人數

gamma = 0.04
S0 = [i for i in range(20000, 40000, 1000)]
beta = [f for f in np.arange(1e-7, 1e-4, 1e-7)]
# 定義偏差函式
def error(res):
    err = (data["感染者"] - res)**2
    errsum = sum(err)
    return errsum

# 窮舉法，找出與實際資料差的平方和最小的S0和beta值
minSum = 1e10
minS0 = 0.0
minBeta = 0.0
bestRes = None

for S in S0:
    for b in beta:
        # 模型的差分方程
        def diff_eqs_2(INP, t):
            Y = np.zeros((3))
            V = INP
            Y[0] = -b * V[0] * V[1]
            Y[1] = b * V[0] * V[1] - gamma * V[1]
            Y[2] = gamma * V[1]
            return Y

        # 數值解模型方程
        INPUT = [S, I0, 0.0]
        RES = spi.odeint(diff_eqs_2, INPUT, t_range)
        errsum = error(RES[:21, 1])
        if errsum < minSum:
            minSum = errsum
            minS0 = S
            minBeta = b
            bestRes = RES
            print("S0=%d beta=%f minErr=%f" % (S, b, errsum))
print("S0 = %d β = %f" % (minS0, minBeta))
 

結果 S0 = 39000, β = 8e-6
上述程式耗時較長，只在探索時執行，完了就註釋掉，用最優引數進行預測。

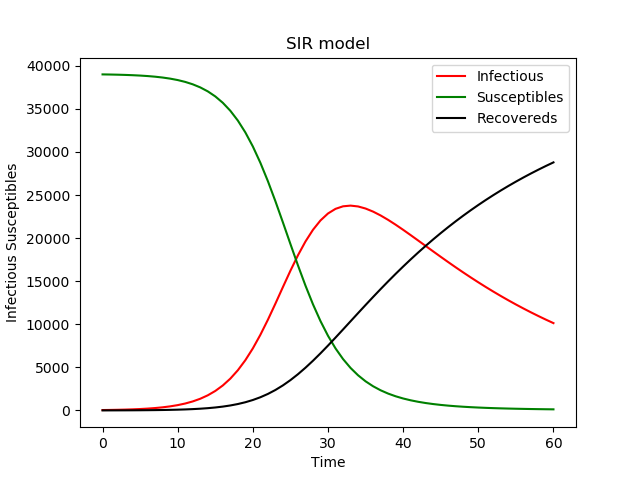
預測最大感染人數:23769 時間是在1月10日的33天后，也就是2月12日。
本文程式碼:https://github.com/zwdnet/2019-nCov-SIRmodel

再次宣告:本文只是我個人在家無聊的遊戲作品，不是正兒八經的預測。我也不是流行病學專業人士。祝疫情早日結束！武漢加油！中國加油！

參考文獻:
[1]SIR模型實現, https://blog.csdn.net/huozi07/article/details/50450433
[2]百度百科SIR模型詞條, https://baike.baidu.com/item/SIR%E6%A8%A1%E5%9E%8B
[3]疫情通報.http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml
[4]計算流行病學. https://www.csdn.net/article/1970-01-01/2816565
[5]關於新型冠狀病毒（2019-nCoV）疫情的《國際衛 生條例（2005）》突發事件委員會會議的宣告. https://www.who.int/zh/news-room/detail/23-01-2020-statement-on-the-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov)
[6]Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. https://www.nejm.org/doi/full/10.1056/NEJMoa2001316?query=featured_home
[7]基於SIR模型對新型冠狀病毒疫情趨勢的簡單分析.https://zhuanlan.zhihu.com/p/104379096

我發文章的四個地方，歡迎大家在朋友圈等地方分享，歡迎點“在看”。
我的個人部落格地址：https://zwdnet.github.io
我的知乎文章地址： https://www.zhihu.com/people/zhao-you-min/posts
我的部落格園部落格地址： https://www.cnblogs.com/zwdnet/
我的微信個人訂閱號：趙瑜敏的口腔醫學學習園