二叉樹的性質
二叉樹的性質
- \(二叉樹的每個節點最多隻有 2 個子樹 (不存在度 >2 的節點) 有左右之分,不可以顛倒\)
- \(二叉樹的第 i 層最多有 2^{i-1}個結點\)
- \(設二叉樹的深度為 k 則: 二叉樹最多有 2^{k}-1 個結點\)
- \(對任何一棵二叉樹 T ,設其葉節點數為 n_{0} 其度為 2 的結點個數為 n_{2} 則:n_{0} = n{2} + 1\)
某些特殊的二叉樹
滿二叉樹:
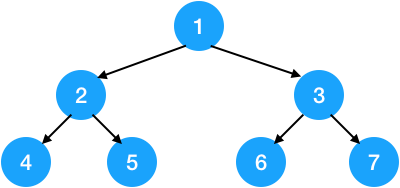
滿二叉樹示意圖
\(深度為 k 且有 2^{k}-1 個結點,就是一棵滿二叉樹,滿二叉樹的每一層都是滿的\)完全二叉樹:
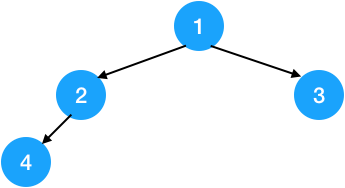
完全二叉樹示意圖
\(除最後一層外,其他層都是滿的,或在右邊連續缺少若干結點,就是一棵完全二叉樹,設有 n 個結點的完全二叉樹的深度為log_{2}(n+1)\)\(深度為 k 的完全二叉樹,至少 2^{k-1} 個結點,最多 2^{k}-1 個結點\)- 二叉搜尋樹:
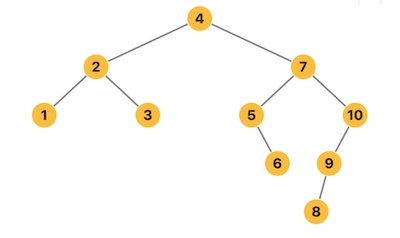
二叉搜尋樹示意圖
排序二叉樹有如下性質- \(若左子樹不空,則左子樹上所有節點均小於根節點的值\)
- \(若右子樹不空,則右子樹上所有節點均大於根節點的值\)
- \(左右子樹也都是二叉搜尋樹\)
- \(二叉搜尋樹可以為空樹\)
遍歷二叉樹
- 先序遍歷 $先序遍歷是指先訪問根節點,再依次訪問左子樹和右子樹$ - 中序遍歷 $中序遍歷是指先訪問左子樹,再依次訪問根節點和右子樹$ - 後序遍歷 $先序遍歷是指先訪問左子樹和右子樹,最後再訪問根節點$ - 層次遍歷 $跟“擴充套件式廣度優先搜尋(俗稱“廣搜”)相同”$ - 四種遍歷參考程式碼: ```cpp
int son[N][2], root;
vector
//先序遍歷
void preorder(int u) {
if (u == 0) return;
v1.push_back(u);
preorder(son[u][0]);
preorder(son[u][1]);
}
//中序遍歷
void inorder(int u) {
if (u == 0) return;
inorder(son[u][0]);
v2.push_back(u);
inorder(son[u][1]);
}
//後序遍歷
void postorder(int u) {
if (u == 0) return;
postorder(son[u][1]);
v3.push_back(u);
}
//層次遍歷
void levelorder() {
queue
if (root != 0) q.push(root);
while (!q.empty()) {
int u = q.front();
q.pop();
v4.push_back(u);
if (son[u][0] != 0) q.push(son[u][0]);
if (son[u][1] != 0) q.push(son[u][1]);
}
}
```
根據遍歷結果復原二叉樹:
注意!先序遍歷和後序遍歷不能確定唯一的二叉樹!
對於先序遍歷和中序遍歷,我們只需在先序遍歷中確定根節點,並且靠中序遍歷找出其位置,再依次還原左子樹和右子樹,即可確定二叉樹。
對於後序遍歷和中序遍歷,也可按照同樣的方法進行還原,確定唯一的二叉樹。
參考程式碼:
// a陣列為中序遍歷,b陣列為先序遍歷
// x1、y1為當前子樹在a陣列中下標的範圍,x2為前子樹在b陣列中下標的起點
int a[N], b[N], son[N][2];
void dfs(int x1, int y1, int x2) {
int pos = x1;
while (a[pos] != b[x2]) { // 在中序遍歷裡找到當前子樹的根
pos++;
}
int len1 = pos - x1, len2 = y1 - pos; // 在中序遍歷裡確定當前子樹的左子樹和右子樹大小
if (len1 > 0) { // 如果有左子樹,那麼根據先序遍歷確定這個節點的左孩子
son[b[x2]][0] = b[x2 + 1];
dfs(x1, pos - 1, x2 + 1); // 遞迴進入左子樹
}
if (len2 > 0) { // 如果有右子樹,那麼根據先序遍歷確定這個節點的右孩子
son[b[x2]][1] = b[x2 + 1 + len1];
dfs(pos + 1, y1, x2 + 1 + len1); // 遞迴進入右子樹
}
}
