【機器學習】演算法原理詳細推導與實現(六):k-means演算法

之前幾個章節都是介紹有監督學習，這個章節介紹無監督學習，這是一個被稱為k-means的聚類演算法，也叫做k均值聚類演算法。

聚類演算法

在講監督學習的時候，通常會畫這樣一張圖：

這時候需要用logistic迴歸或者SVM將這些資料分成正負兩類，這個過程稱之為監督學習，是因為對於每一個訓練樣本都給出了正確的類標籤。

在無監督學習中，經常會研究一些不同的問題。假如給定若干個點組成的資料集合：

所有的點都沒有像監督學習那樣給出類標籤和所謂的學習樣本，這時候需要依靠演算法本身來發現資料中的結構。在上面的這張圖中，可以很明顯的發現這些資料被分成了兩簇，所以一個無監督學習演算法將會是聚類演算法，演算法會將這樣的資料聚整合幾個不同的類。

聚類演算法很多應用場景，舉幾個最常用的：

1. 在生物學應用中，經常需要對不同的東西進行聚類，假設有很多基因的資料，你希望對它們進行聚類以便更好的理解不同種類的基因對應的生物功能
2. 在市場調查中，假設你有一個數據庫，裡面儲存了不同顧客的行為，如果對這些資料進行聚類，可以將市場分為幾個不同的部分從而可以對不同的部分指定相應的銷售策略
3. 在圖片的應用中，可以將一幅照片分成若干個一致的畫素子集，去嘗試理解照片的內容
4. 等等...

聚類的基本思想是：給定一組資料集合，聚整合若干個屬性一致的類。

k-means聚類

這個演算法被稱之為k-means聚類演算法，用於尋找資料集合中的類，演算法的輸入是一個無標記的資料集合\({x^{(1)},x^{(2)},...,x^{(m)}}\)，因為這是無監督學習演算法，所以在集合中只能看到\(x\)，沒有類標記\(y\)。k-means

step 1 隨機選取k個聚類質心點(cluster centroids)，那麼就等於存在了\(k\)個簇\(c^{(k)}\)：

\[ \mu_1,\mu_2,...,\mu_k \in R^n \]

step 2 對於每一個\(x^{(i)}\)，需要計算與每個質心\(\mu_j\)的距離，\(x^{(i)}\)則屬於與他距離最近質心\(\mu_j\)的簇\(c^{(j)}\)：

\[ c^{(j)}:=argmin_j||x^{(i)}-\mu_j||^2,j \in 1,2,...,k \]

step 3 對於每一個類\(c^{(j)}\)，重新計算該簇質心的值：

\[ \mu_j:=\frac{\sum^m_{i=1}l\{c^{(i)}=j\}x^{(i)}}{\sum^m_{i=1}l\{c^{(i)}=j\}} \]

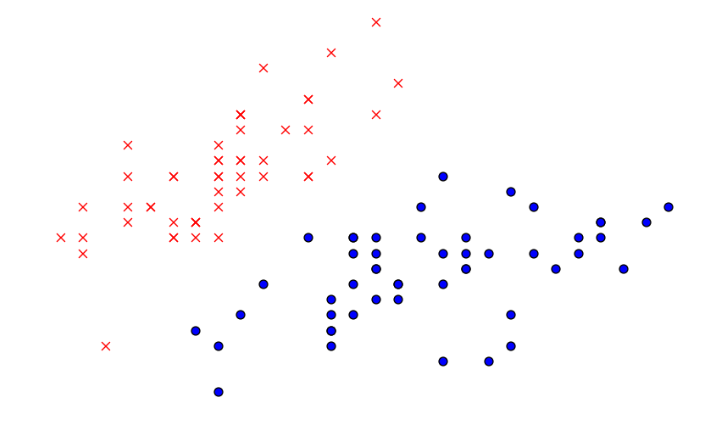
之後需要重複step 2和step 3直到演算法收斂，下面圖中對上述步驟進行解釋，存在資料點如下所示：

假設我們取\(k=2\)，那麼會在資料集合中隨機選取兩個點作為質心，即下圖中紅色的點\(\mu_1\)和藍色的點\(\mu_2\)：

分別計算每一個\(x^{(i)}\)和質心\(\mu_1\)、\(\mu_2\)的距離，\(x^{(i)}\)離哪個\(\mu_j\)更近，那麼\(x^{(i)}\)就屬於哪個\(c^{(j)}\)，即哪些點離紅色\(\mu_1\)近則屬於\(c^{(1)}\)，離藍色近則屬於\(c^{(2)}\)。第一次將\(x^{(i)}\)分類後效果如下：

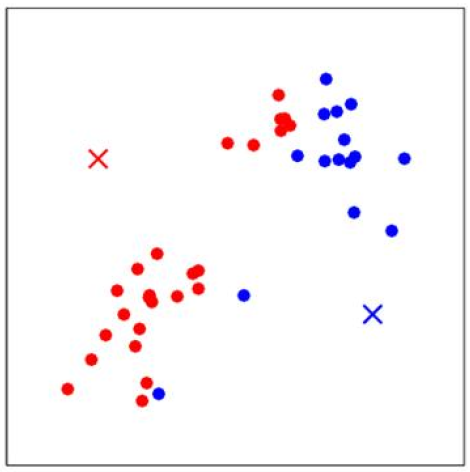
下一步是更新簇\(c^{(j)}\)的質心，計算所有紅色點的平均值，得到新的質心\(\mu_{1\_new}\)；計算所有藍色點的平均值，得到新的質心\(\mu_{2\_new}\)，如下圖所示：

再次重複計算每一個\(x^{(i)}\)和質心的距離，更新質心的值。多次迭代收斂後，即使進行更多次的迭代，\(x^{(i)}\)的類別和質心的值都不會再改變了：

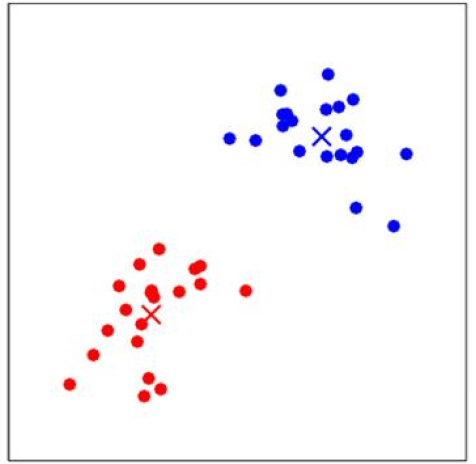
這裡涉及到一個問題，如何保證k-means是收斂的？前面演算法強調的是結束條件是收斂，為了保證演算法完全收斂，這裡引入畸變函式(distortion function)：

\[ J(c,\mu)=\sum^m_{i=1}||x^{(i)}-\mu_{c^{(i)}}||^2 \]

\(J(c,\mu)\)表示每個樣本點\(x^{(i)}\)到其質心距離的平方和，當\(J(c,\mu)\)沒有達到最小值，可以固定\(c^{(j)}\)更新每個簇的質心\(\mu_j\)，質心變化後固定質心的值\(\mu_j\)重新劃分簇\(c^{(j)}\)也變化，不斷迭代。當\(J(c,\mu)\)達到最小值時，\(\mu_j\)和\(c^{(j)}\)也同時收斂。(這個過程和前面【機器學習】演算法原理詳細推導與實現(五):支援向量機(下)中的SMO優化演算法演算法的過程很相似，都是固定一組值或者一個值，更新另外一組或者一個值，使其函式優化到極值，這個過程叫做座標上升，這裡不作推導)。實際上可能會有多組\(\mu\)和\(c\)能夠使得\(J(c,\mu)\)取得最小值，但是這種情況並不多見。

由於畸變函式\(J(c,\mu)\)是非凸函式，所以意味著不能保證取的最小值是全域性最小值，也就是說k-means對隨機取的質心的初始位置比較敏感。一般達到區域性最優已經滿足分類的需求了，如果比較介意的話，可以多跑幾次k-means演算法，然後取\(J(c,\mu)\)最小值的\(\mu\)和\(c\)。

k值確定

很多人不知道怎麼確定資料集需要分多少個類(簇)，因為資料是無監督學習演算法，k值需要認為的去設定。所以這裡會提供兩種方法去確定k值。

第一種方法：

觀察法，本文的例子可以看出，把資料集畫在圖中顯示，就能很明顯的看到應該劃分2個類(簇)：

並非所有的資料都像上面的資料一樣，一眼可以看出來分2個類(簇)，所以介紹一般比較常用的第二種方法。

第二種方法：

輪廓係數（Silhouette Coefficient），是聚類效果好壞的一種評價方式。最早由 Peter J. Rousseeuw 在 1986 提出。它結合內聚度和分離度兩種因素。可以用來在相同原始資料的基礎上用來評價不同演算法、或者演算法不同執行方式對聚類結果所產生的影響。

按照上面計算k-means演算法的步驟計算完後，假設\(x^{(i)}\)屬於簇\(c^{(i)}\)，那麼需要計算如下兩個值：

1. \(a(i)\)，計算\(x^{(i)}\)與同一簇中其他點的平均距離，代表\(x^{(i)}\)與同一簇中其他點不相似的程度
2. \(b(i)\)，計算\(x^{(i)}\)與另一個與\(x^{(i)}\)最近的簇\(c\)，與簇\(c\)內所有點平均距離，代表\(x^{(i)}\)與最相鄰簇\(c\)的不相似程度

最終輪廓係數的計算公式為：

\[ S(i)=\frac{b(i)-a(i)}{max(a(i),b(i))} \]

輪廓係數的範圍為\([-1, 1]\)，越趨近於1代表內聚度和分離度都相對較優。

所以可以在k-means演算法開始的時候，先設定k值的範圍\(k \in [2, n]\)，從而計算k取每一個值的輪廓係數，輪廓係數最小的那個k值就是最優的分類總數。

例項

假設存在資料集為如下樣式：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn import metrics

# figsize繪圖的寬度和高度，也就是畫素
plt.figure(figsize=(8, 10))
x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
# print(X)

# x,y軸的繪圖範圍
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('sample')
plt.scatter(x1, x2)
# 點的顏色
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'b']
# 點的形狀
markers = ['o', 's', 'D', 'v', '^', 'p', '*', '+']
plt.show()

雖然觀察法可以知道這個資料集合只要設定\(k=3\)就好了，但是這裡還是想用輪廓係數來搜尋最佳的k值。假設不知道的情況下，這裡取\(k \in [2, 3, 4, 5, 8]\)：

# 測試的k值
tests = [2, 3, 4, 5, 8]
subplot_counter = 1
for t in tests:
    subplot_counter += 1
    plt.subplot(3, 2, subplot_counter)
    kmeans_model = KMeans(n_clusters=t).fit(X)
    for i, l in enumerate(kmeans_model.labels_):
        plt.plot(x1[i], x2[i], color=colors[l], marker=markers[l], ls='None')
        # 每個點對應的標籤值
        # print(kmeans_model.labels_)
        plt.xlim([0, 10])
        plt.ylim([0, 10])
        plt.title('K = %s, Silhouette Coefficient = %.03f' % (t, metrics.silhouette_score(X, kmeans_model.labels_, metric='euclidean')))

得到的結果為：

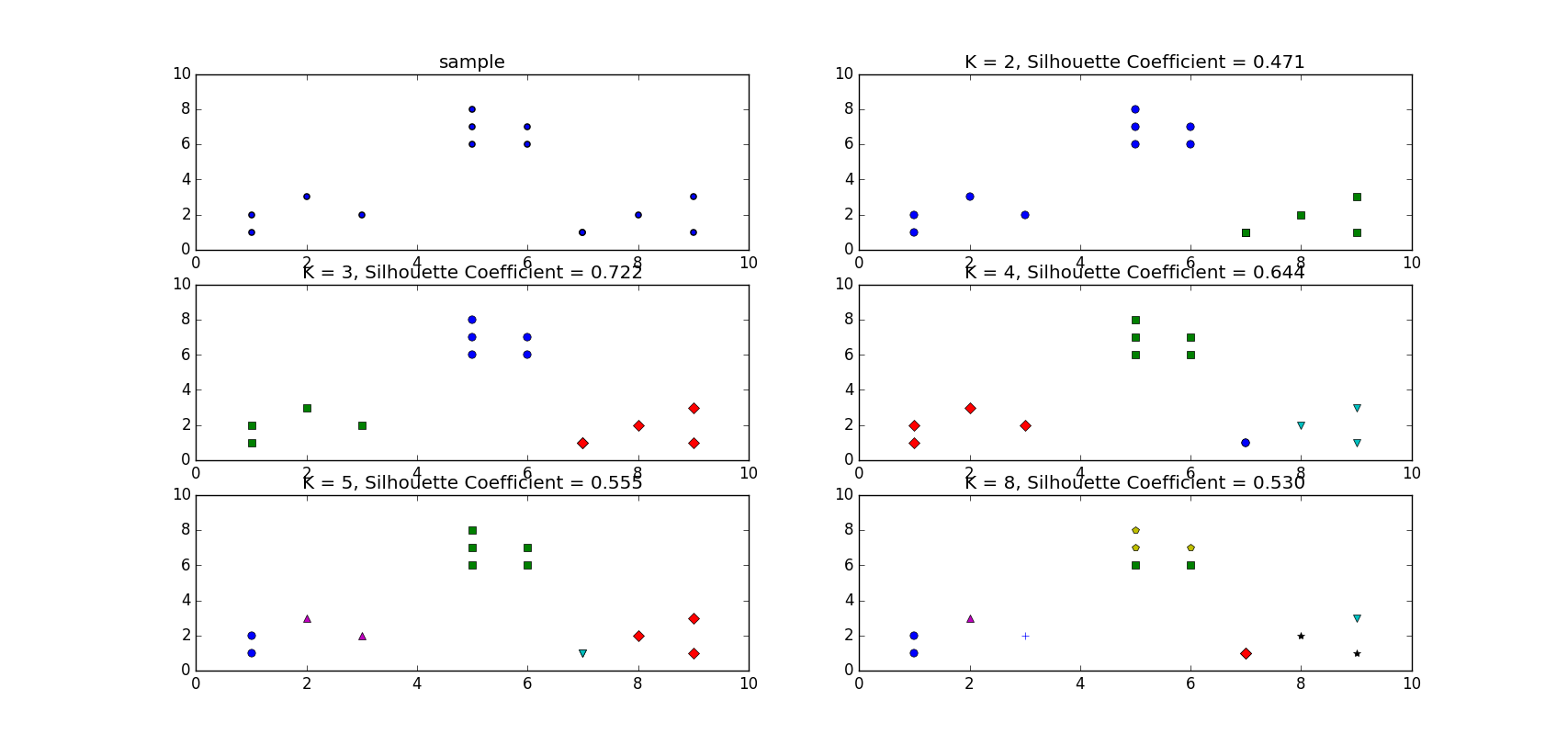
可以看到當\(k=3\)時輪廓係數最大為0.722

資料和程式碼下載請關注公眾號【 機器學習和大資料探勘 】，後臺回覆【 機器學習 】即可獲