剛開學便被拉去參加了研究生數模比賽，賽題是一個航班排班的優化問題，所以第一反映便是遺傳演算法，比賽期間三個問題都使用單目標遺傳演算法，趁著還比較熟悉，特此記錄，以便後續複習。本篇文章使用Python進行實現。 ## 啟發式演算法 > 啟發式演算法是一種技術，這種技術使得在可接受的計算成本內去搜尋最好的解，但不一定能保證所得的可行解和最優解，甚至在多數情況下，無法闡述所得解同最優解的近似程度。 就是說這種演算法的全域性最優解只是理論上可行，大多數情況下都是一個區域性最優解。啟發式演算法用的比較多的有模擬退火演算法(SA)、遺傳演算法(GA)、列表搜尋演算法(ST)、進化規劃(EP)、進化策略(ES)、蟻群演算法(ACA)、人工神經網路(ANN)。這裡重點介紹一下遺傳演算法(GA)。 ## 遺傳演算法準備 > 遺傳演算法（Genetic Algorithm, GA）起源於對生物系統所進行的計算機模擬研究。它是模仿自然界生物進化機制發展起來的隨機全域性搜尋和優化方法，借鑑了達爾文的進化論和孟德爾的遺傳學說。其本質是一種高效、並行、全域性搜尋的方法，能在搜尋過程中自動獲取和積累有關搜尋空間的知識，並自適應地控制搜尋過程以求得最佳解。 具體來說，在寫演算法之前，有四個很重要的步驟： 1. 確定編碼方式 2. 如何設計編碼 3. 確定約束條件 4. 如何實現約束 ### 確定編碼方式 對於編碼方式來說，影響到交叉運算元、變異運算元等遺傳運算元的運算方法，大很大程度上決定了遺傳進化的效率。 總的來說，編碼方式可以分為三大類：二進位制編碼法、浮點編碼法、符號編碼法。 1. 二進位制編碼法：將求解的數從十進位制轉換成二進位制表示，這樣便於編碼與解碼，方便交叉和變異運算元的實現，但對於一些連續函式的優化問題，由於其隨機性使得其區域性搜尋能力較差，如對於一些高精度的問題，當迭代接近最優解後，由於其變異後表現型變化很大，不連續，所以會遠離最優解，達不到穩定。而格雷碼能有效地防止這類現象。 2. 格雷碼編碼法：我們先來複習一下格雷碼： ``` 十進位制　格雷碼 二進位制 0 0000 0000 1 0001 0001 2 0011 0010 3 0010 0011 4 0110 0100 5 0111 0101 6 0101 0110 7 0100 0111 8 1100 1000 9 1101 1001 10 1111 1010 ``` 維基百科對格雷碼解決誤碼的說明: > 傳統的二進位系統例如數字3的表示法為011，要切換為鄰近的數字4，也就是100時，裝置中的三個位元都得要轉換，因此於未完全轉換的過程時裝置會經歷短暫的，010,001,101,110,111等其中數種狀態，也就是代表著2、1、5、6、7，因此此種數字編碼方法於鄰近數字轉換時有比較大的誤差可能範圍。葛雷碼的發明即是用來將誤差之可能性縮減至最小，編碼的方式定義為每個鄰近數字都只相差一個位元，因此也稱為最小差異碼，可以使裝置做數字步進時只更動最少的位元數以提高穩定性。 連續兩個整數所對應的編碼值之間僅僅只有一個碼位是不同的，當迭代次數很多接近最優值時，相鄰兩個值之間變化是最大的，當一個染色體變異後，它原來的表現現和現在的表現型是連續的，這樣可以將誤差的可能性縮減至最小。 格雷碼的轉換為: G為格雷碼，B為二進位制碼，n為當前計算位，$\oplus$為異或 就有$G(n) = B(n+1) \oplus B(n)$ 即$G(n) = B(n+1) + B(n)$ 3. 浮點編碼法 對於一些多維、高精度要求的連續函式優化問題，使用二進位制編碼來表示個體時將會有一些不利之處。 二進位制編碼存在著連續函式離散化時的對映誤差。個體長度較知時，可能達不到精度要求，而個體編碼長度較長時，雖然能提高精度，但卻使遺傳演算法的搜尋空間急劇擴大。 所謂浮點法，是指個體的每個基因值用某一範圍內的一個浮點數來表示。在浮點數編碼方法中，必須保證基因值在給定的區間限制範圍內，遺傳演算法中所使用的交叉、變異等遺傳運算元也必須保證其運算結果所產生的新個體的基因值也在這個區間限制範圍內。 4. 符號編碼法 這種編碼法其實在解決實際問題時問題時是用的最多的，例如這次的航班優化問題我就使用的這種方法，這種方法要結合實際問題來進行編碼，然後交叉和變異也要結合實際進行編寫，這裡我就舉個具體例子來講解一下符號編碼法。 ### 如何設計編碼 對於一般的數學函式優化問題都是將求解的值轉換成二進位制或者格雷碼進行迭代然後計算適應度(fitness)即可，這裡我主要講解一下如果不是一個傳入值直接求解方程的問題解決。 舉個栗子 假如我有10架航班(a,b,c,...)，和5個登機口(1,2,3,4,5)，我現在要讓排班更加緊湊，使得使用的登機口數儘量少。每架飛機有個一個出發時間(departure_time)，在出發時間之前45分鐘飛機必須到達登機口，於是我們設計的一個最小化函式即為 $$ F = \sum_{i=0}^5\sum_{j=0}^{10}S_{ij}$$ 這裡i即為登機口數，j為航班數，這樣$S_ij$就是對應登機口的航班與上一架航班的時間之差，使得時間和最小我們可以使得安排更加緊湊。 那我就可以這樣進行編碼  10個染色體就是對應的10架航班，裡面的內容就是其對應的登機口號，這樣我們就可以計算同一登機口的相鄰飛機的起飛間隔時間差了。 例如2號登機口對應的就是飛機a，飛機i，那麼我們使用$ i_{arrival\_time} - a_{arrival\_time}$就可以得到對應的時間差了，統計計算1號，3號，4號和5號，加在一起就是我們的目標函式的值了。 ### 確定約束條件 對於不同的問題求解會有不同的約束方式，常見的約束方式有 - 範圍限制 - 條件限制 **範圍限制**，例如我們的求值只可在(0,0.3]與[0.5,0.8)之間，那麼我們在求解的時候要麼加入懲罰項，即計算到非對應範圍的時候乘上一個很大的值來限制，要不就在對應交叉和變異的時候先判斷在交叉變異進行限制。 **條件限制**，例如上題，我們假如約束條件，即為飛機有寬與窄之分，我們的登機口也有對應的寬窄之分，對應的飛機只能停到對應的登機口處，所以這裡我們編碼時也要在滿足約束進行編碼，編寫交叉變異時也針對此進行編寫。 ### 如何實現約束 實現約束即在三個地方實現，分別為 1. 基因可行解初始化(inital) 2. 基因交叉(crossover) 3. 基因變異(mutate) 這裡簡單講解一下可行解初始化的約束如何實現，我們可以寫一個簡單的while迴圈來找到可行解: ```python POP_SIZE = 100 # 可行解數目 DNA_SIZE = 10 #dna長度，這裡為航班數量，即為10 all_airport_id = [1,2,3,4,5] # 登機口id aircraft_to_airport_dict = { 1:[1,2,3], 2:[2,3,4], ... }# 這裡是每架飛機對應的登機口id,這裡我就簡寫了 def inital(self): pop = [] # 可行解list while len(pop) != POP_SIZE: dna = [0 for i in range(DNA_SIZE)] all_aircraft_id = list(range(1, 11)) # 所有飛機id temp_airport_id_set = set() # 遍歷過的儲存飛機對應的可行的飛機場 for aircraft_id in all_aircraft_id: workable_airport = aircraft_to_airport_dict[aircraft_id] #可行的登機口id while 1: #直到要找到合適的機場停機 airport_id = random.choice(list(workable_airport)) # 隨機生成一個登機口id temp_airport_id_set.add(airport_id) if len(temp_airport_id_set) == len(workable_airport): dna[aircraft_id-1] = 0 #如果全都不合適，就跳出 break if constraint(aircraft_id, airport_id): #如果滿足約束 dna[aircraft_id-1] = airport_id ``` 這裡的constraint約束函式可以是很多約束，比如時間約束，區域約束等等。 ## 遺傳演算法實現 個人認為遺傳演算法總體分為5個部分: 1. 初始化可行解 2. 目標函式，即計算適應度(fitness) 3. 適者生存 4. 交叉進化 5. 變異 具體流程為: ``` 生成n組可行解dna 迭代m次： 計算每個dna的fitness 適者生存 迴圈n個dna: 交叉進化 變異 ``` 接下來主要講一下適者生存、交叉進化和變異 ### 適者生存 > 物競天擇，適者生存 適者生存的意思就是通過計算fitness，然後作為隨機選擇的概率，這樣概率越大的就被選擇到概率越大。具體實現如下，我對fitness做了個倒數，這裡是因為我計算的是最小化，所以越小對於我來說是最優的，所以取倒數再計算概率才符合邏輯。 ```python def select(self, pop, fitness): fitness = 1 / fitness idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True, p=fitness/fitness.sum()) return pop[idx] ``` ### 交叉進化 交叉進化有很多種方式，具體可以看這篇文章[遺傳演算法中幾種交叉運算元小結](https://blog.csdn.net/u012750702/article/details/54563515),講的已經很全了。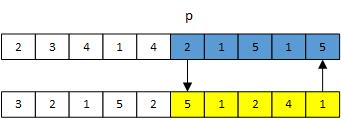 這裡我主要講一下單點交叉，即隨機在雙親(parent)dna上選擇一個點p，然後與孩子(child)dna上p點後的基因進行交換，實現起來也十分簡單。如下圖，o點為2，然後就將將藍色部分與黃色部分互相交換。  ```python CROSS_RATE = 0.8 #交叉概率 def crossover(self, parent, pop): if np.random.rand() < CROSS_RATE: i_ = random.randint(0, POP_SIZE - 1) # 孩子基因,child p = np.random.randint(0, DNA_SIZE) # 單點交叉 parent[p:DNA_SIZE] = pop[i_][p:DNA_SIZE] return parent return parent ``` ### 變異 > 人間總有那麼多出其不意的突變，很難說我們怎樣才算是到了窮途末路，人只要一息尚存，對什麼都可抱有希望。 > > ——蒙田《蒙田隨筆全集》 > 許多突變都是中性的，但有些可能會對後代造成損傷，而有些則可能是有益的。控制基因的突變可以對生物體造成極大的影響。有益的基因突變可以幫助生物更好地適應環境，並很可能遺傳給後代。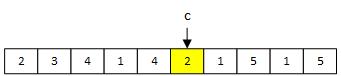 變異就是在dna上隨機選擇一個點進行基因變異，這樣做的原因是防止區域性最優，因為如果這個世界有人突變，那麼就不排除會比我們現在更加適應這個世界的可能。c點就是變異點。  ```python MUTATION_RATE = 0.01 #突變概率 def mutate(self, child): for c in range(DNA_SIZE): if np.random.rand() < MUTATION_RATE: workable_airport = aircraft_to_airport_dict[aircraft_id] #可行的登機口id random_airport_id = random.choice(workable_airport) #隨機一個機場 child[c] = random_airport