《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》論文閱讀
背景簡介
GCN的提出是為了處理非結構化資料(相對於image畫素點而言)。CNN處理規則矩形的網格畫素點已經十分成熟,其最大的特點就是利用卷積進行①引數共享②區域性連線,如下圖:
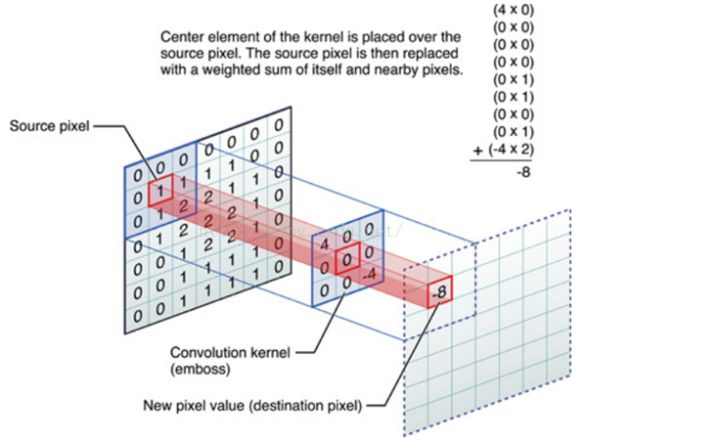
那麼類比到非結構資料圖(graph),CNN能直接對非結構資料進行同樣類似的操作嗎?如果不能,我們又該採用其他什麼方式呢?
首先思考能不能,答案是不能。至少我們無法將graph結構的資料規整到如上圖所示的矩形方格中,否則結點之間的邊無法很好表示。還可以考慮卷積核這一點,我們知道不管我的圖(image)如何變化(圖片變大或變小,圖中狗數量多一隻),我們設計好的提取特徵的卷積核都不需要變化,但是試想,graph還能這樣嗎,照貓畫虎(就是隨意猜想),如果我們也設計和圖一樣的卷積核,如下圖。可見怎麼設計可複用發提取有效特徵的卷積核就不能單純從拓撲結構上考慮。
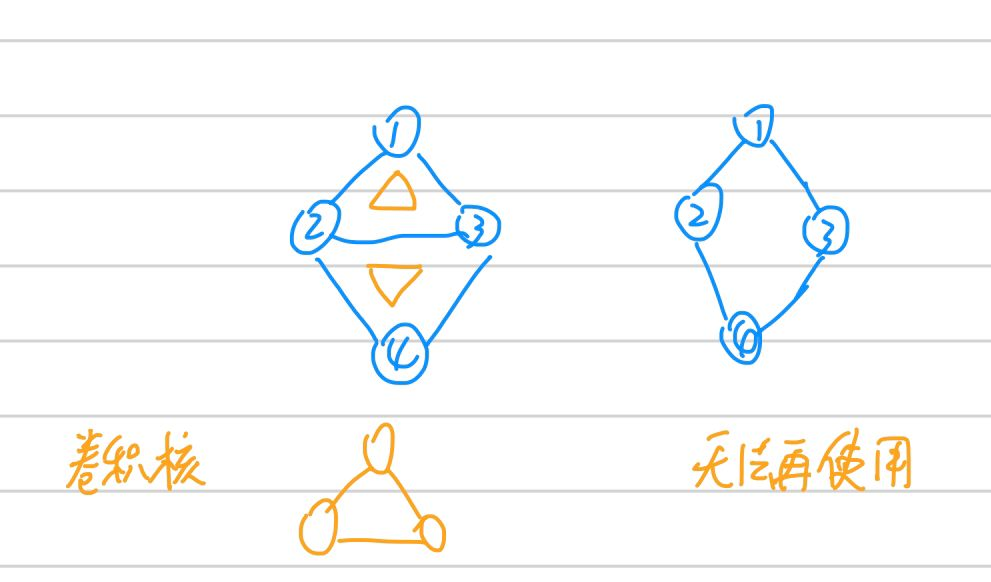
GCN卷積思路
那麼人們(這方面的研究在很早之前就有,這篇文章也算是“集大成者+新的idea”)如何考慮在Graph上進行卷積呢?總的來說分為兩種
①spatial domain
大致瞭解了下,抽象來看,和CNN算是有點異曲同工的味道。具體論文還沒看過,先不展開細說。
②spectral domain
這篇論文就是從譜方法展開的,這就同spatial角度差了挺遠的了。其靈感應該是從訊號處理的傅立葉變換時域與頻域轉換而來,後文詳細說明。
傅立葉變換
回顧高數中的傅立葉變換,傅立葉的理論依據就是任何週期非週期(即週期無窮)的的函式都可以由一組正交基($cosx,sinx$)函式通過線性組合表示。然後通過尤拉公式,進一步轉換得到如下傅立葉變換和逆變換:

其中逆變換中$F(w)$就是$f(t)$第一個等式基函式的係數。
從訊號處理角度來說,可以理解成將一個周期函式,從時域角度分解成了頻域角度,如下動圖
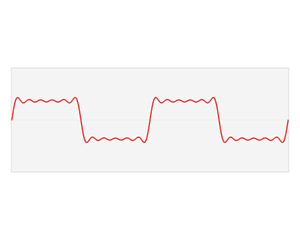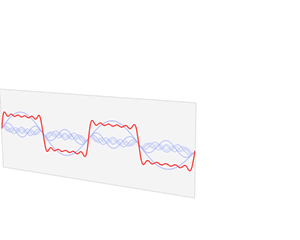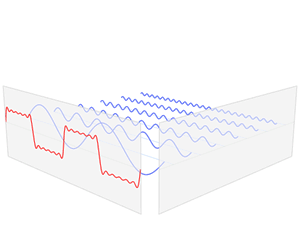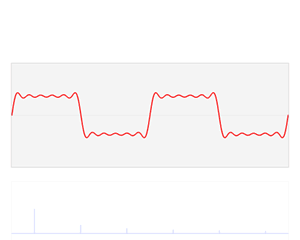

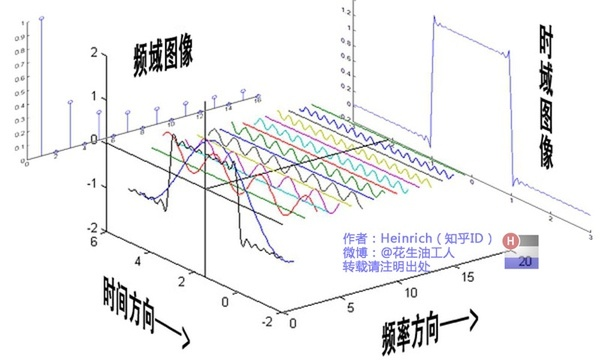
傅立葉變換函式的基
傅立葉變換的關鍵點就是,我們通過一組函式的基:三角函式系。類似於空間向量中,我們通過一組基的線性組合,可以表示改空間相中的任何一個向量。

以上,我們只需要知道的就是傅立葉變換是什麼,使用了基本函式基的原理
卷積定理
卷積定理:卷積定理是傅立葉變換滿足的一個重要性質。卷積定理指出,函式卷積的傅立葉變換是函式傅立葉變換的乘積。換句話說,$$F(f\star g)
$$F^{-1}{\begin{Bmatrix}
F(f\star g)
\end{Bmatrix}}
=F^{-1}\begin{Bmatrix}
F(f)\cdot F(g)
\end{Bmatrix} \\
f\star g
=F^{-1}\begin{Bmatrix}
F(f)\cdot F(g)
\end{Bmatrix}$$
所以,我們求兩個函式的卷積的時候,可以分別求兩個函式的傅立葉變換,然後再做一次逆傅立葉變換得到
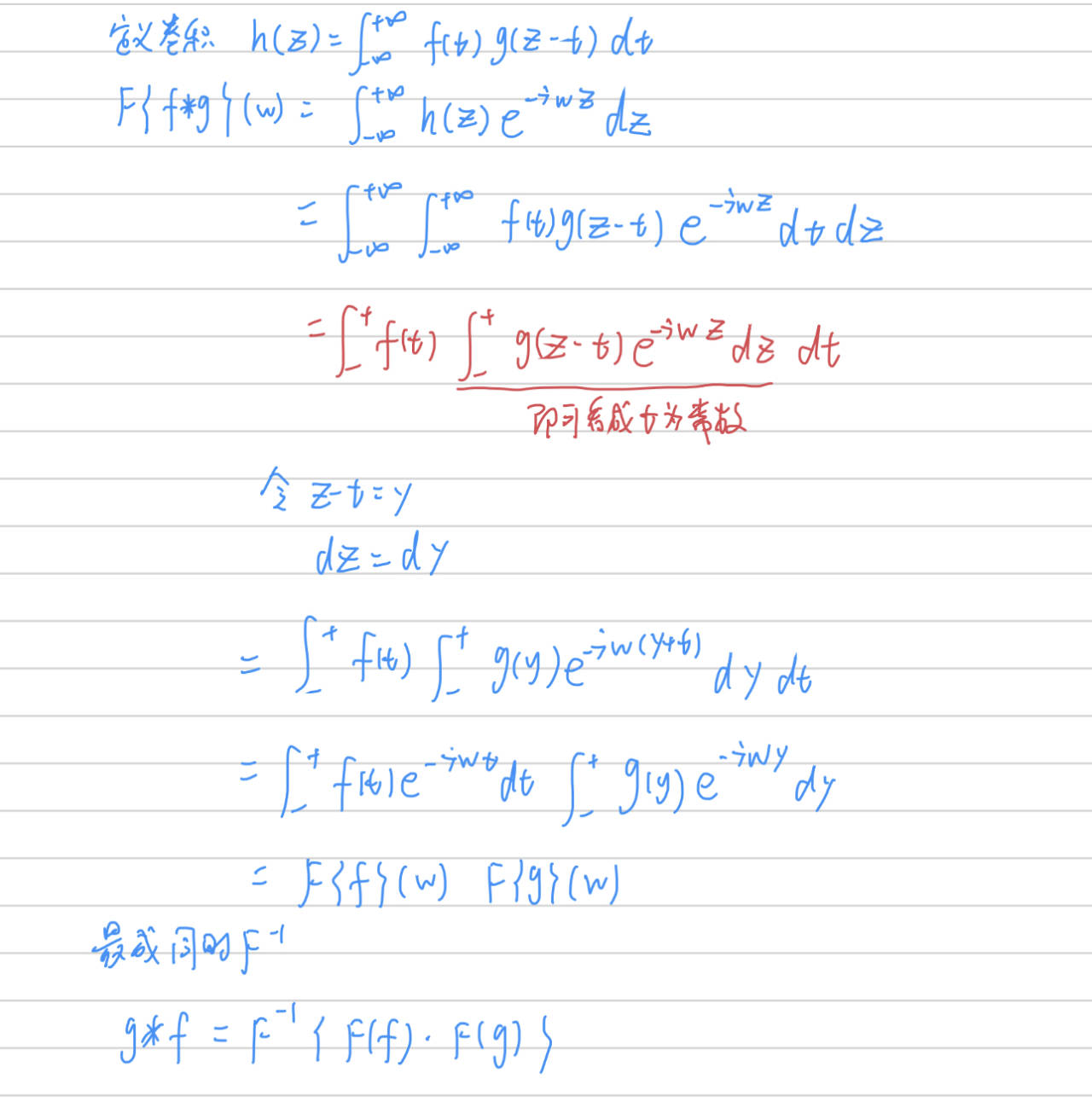
拉普拉斯矩陣
拉普拉斯矩陣的由來是從譜聚類說起,下面是幾種場見的拉普拉斯矩陣形式
拉普拉斯矩陣定義
對於圖$G=(V, E)$,拉普拉斯的普通形式是$$L=D-A$$,其中$D$是對角頂點度矩陣(零階矩陣的一行和),$A$是圖的鄰接矩陣,如下圖

$L$中的元素分別為:
$$L_{i,j}=\left\{\begin{matrix}
&diag(v_{i}) &i=j \\
&-1 &i\neq j\,\,and\,\,v_{i}\,\,is\,\,adjacent\,\,to\,\,v_{j} \\
&0 &otherwise
\end{matrix}\right.$$
對稱歸一化的拉普拉斯矩陣(Symmetric normalized Laplacian)
$$L^{sys}=D^{-1/2}LD^{-1/2}=I-D^{-1/2}AD^{-1/2}$$
其中$L$的各項內容為:
$$L^{sys}_{i,j}=\left\{\begin{matrix}
&1 &i=j\,and\,\,diag(v_{i})\neq 0 \\
&-\frac{1}{\sqrt{diag(v_{i})diag(v_{j})}} \,\,\,\,&i\neq j\,\,and\,\,v_{i}\,\,is\,\,adjacent\,\,to\,\,v_{j} \\
&0 &otherwise
\end{matrix}\right.$$
隨機遊走歸一化拉普拉斯矩陣(Random walk normalized Laplacian)
$$L^{rw}=D^{-1}L=I-D^{-1}A$$
其中$L$的各項內容為:
$$L^{rw}_{i,j}=\left\{\begin{matrix}
&1 &i\neq j\,and\,\,diag(v_{i})\neq 0 \\
&-\frac{1}{diag(v_{i})} \,\,\,\,&i\neq j\,\,and\,\,v_{i}\,\,is\,\,adjacent\,\,to\,\,v_{j} \\
&0 &otherwise
\end{matrix}\right.$$
無向圖拉普拉斯的性質
①拉普拉斯矩陣是實對稱矩陣,可以對角化
②拉普拉斯矩陣是半正定的(譜聚類中可以根據定義證明$f(x)=x^{T}Ax$,對於任意$x\neq 0$,均有$f(x)\geq 0$)
③最小特徵值是0(半正定),對於的特徵向量是$1$,容易驗證$L1=01$
拉普拉斯矩陣譜分解
根據上一條拉普拉斯矩陣的性質,是對稱的,所以一定可以進行對角化,也就是找到一堆正交基
$$L=U\begin{pmatrix}
&\lambda _{1} & &\\
& &\ddots &\\
& & &\lambda _{n}
\end{pmatrix}U^{-1}$$
且其中$U$是單位矩陣,$$UU^{T}=I$$
拉普拉斯運算元
拉普拉斯運算元的定義是:
$$\bigtriangleup f=\sum \frac{\partial f}{\partial ^{2}x}$$
是由散度推導而來的,上式是$f$對$x$求二階偏導。那麼回憶數字影象處理中離散情況下:
| $f(x-1,y)$ | ||
| $f(x,y-1)$ | $f(x,y)$ | $f(x,y+1)$ |
| $f(x+1,y)$ |
$$\begin{aligned} \Delta f &= \frac{\partial f}{\partial ^{2}x} + \frac{\partial f}{\partial ^{2}y} \\ &=f(x+1,y) + f(x-1,y) - 2f(x,y) + f(x, y+1)+f(x,y-1)-2f(x,y) \\ & = f(x+1,y) + f(x-1,y) + f(x, y+1)+f(x,y-1)-4f(x,y) \end{aligned}$$
也就是說,拉普拉斯運算元可以描述某個結點進行擾動之後,相鄰結點變化的總收益
那麼進行推廣:我們希望能將拉普拉斯運算元用到graph中,希望能衡量一個結點變化之後,對其他相鄰結點的干擾總收益
所以,當某點發生變化時,只需要將所有相鄰的點相加再減去該中心點*相鄰個數(與上面方格計算二階偏導類似) 。

而拉普拉斯矩陣$L=D-W$,所以$$\Delta f=(D-W)f=L\cdot f$$,其中$f$是$N*M$代表$N$個結點和每個結點$M$維特徵。
而圖$D-W=L$恰好是拉普拉斯矩陣。這就是為什麼GCN中使用拉普拉斯矩陣$L=D-W$(差負號)的原因:需要對圖$f$做拉普拉斯變換,等同於$L\cdot f$
$\Delta = L = D-W$
圖上的傅立葉變換
首先,我們的目標始終是要對圖 $f$ 做卷積操作,假設卷積核為 $g$,而根據卷積定理有$$ f\star g =F^{-1}\begin{Bmatrix} F(f)\cdot F(g) \end{Bmatrix}$$所以,我們重點需要計算$F(f)$,而$F(g)$就可以當作引數去訓練,那麼如何計算出前者呢?
類比數學上傅立葉的思路,是需要找到一組正交的函式基,那麼同理現在對於圖(graph) $f$ , 我們也需要找到一組定義在圖上的正交基,而上文已經解釋了圖上的拉普拉斯矩陣$L$ 天然可譜分解,也就是對角化找到一組正交基
$$LU=\lambda U \,\,\,\,\,\,\,UU^{T}=UU^{-1}=I$$
同時可以證明$$\Delta e^{-iwt} = \frac{\partial e^{-iwt}}{\partial ^{2}t} = - w^2 e^{-iwt} $$
$e^{-iwt}$ 就是變換 $\Delta $ 的特徵函式,$w$和特徵值密切相關。而又因為$LU=\lambda U$,所以我們類比 $U$ 等同於 $e^{-iwt} $,也就是找到了圖上的一組正交基($L$的特徵向量)。
$$ F(\lambda _{l})=\hat{f}(\lambda _{l})=\sum_{i=1}^{N}f(i)u^{*}_{l}(i)$$
$f$ 是 graph 上的 $N$ 維向量,$f(i)$ 與graph的頂點一一對應,$u_{l}(i)$ 表示第 $l$ 個特徵向量的第 $i$ 個分量。那麼特徵值(頻率)$\lambda _{l}$ 下的,$f$ 的graph 傅立葉變換就是與 $\lambda _{l}$ 對於的特徵向量 $u_{l}$ 進行內積運算。所以圖$f*u^{*}_{l}$ 得到一個離散的值,如我們常見到的頻域下的一個幅度值。
===>推廣到矩陣下形式:

其中左邊的是傅立葉變換,右邊的$u_{i}(j) $表示第 $i$ 個特徵向量的第 $j$ 維,所以圖 $f$ 的傅立葉變換可以寫成$$\hat{f} = U^{T} f$$,其中$U^T$是$L$的特徵向量,也即是當前空間的一組基
圖上的逆傅立葉變換

內容彙總:拉普拉斯矩陣/運算元,傅立葉變換,GCN
前面介紹了傅立葉變換,又提到了拉普拉斯矩陣/運算元,這和GCN有什麼關係呢?
現在我們可以進一步考慮具體的卷積了,也就是 $$ f\star g =F^{-1}\begin{Bmatrix} F(f)\cdot F(g) \end{Bmatrix}$$
其中$$F(f) = \hat{f} = U^Tf$$
而 $F(g)$ 是卷積核$g$ 的傅立葉變換,我們可以寫成對角線形式(為了矩陣相乘),$\bigl(\begin{smallmatrix}
\hat{h}(\lambda 1) & & &\\
& & \ddots & \\
& & &\hat{h}(\lambda n)
\end{smallmatrix}\bigr)$
其中
所以兩者的傅立葉變換乘機為: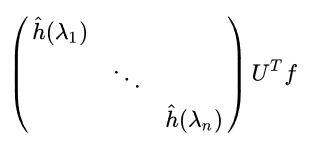
再照顧最外層的$F^{-1}{}$,那就是再左乘$U$:$$(f\star g)=U\begin{pmatrix}
&\hat{h}(\lambda_{1}) & \\
& &\ddots \\
& & &\hat{h}(\lambda_{n})
\end{pmatrix}U^{T}f$$

以上,我們算是完整得到了如何再圖上做卷積的公式:先得到圖的拉普拉斯矩陣$L$,得到$L$的對應特徵向量$U$
圖卷積的改進
上文我們已經知道了 $f\star g$的計算,但是其中一個問題就是$L$矩陣的特徵向量$U$計算是費時的複雜度太高
所以提出如下近似多項式形式$$\hat{h}(\lambda_{l})\approx \sum_{K}^{j=0}\alpha _{j}\lambda^{j}_{l}$$
也就是:

最後卷積變成了:
$$y_{out}= \sigma(\sum_{j=0}^{K-1} \alpha _{j}L^{j}x)$$
這樣就不需要進行特徵值分解,直接使用$L^{j}$,即拉普拉斯矩陣的階數
改進一
其實是進一步簡化,將上式$L^{j}$使用切比雪夫展開式來近似,首先將上式$$\boldsymbol{g}_{\boldsymbol{\theta^{\prime}}}(\boldsymbol{\Lambda}) \approx \sum_{k=0}^K \theta_k^{\prime} T_k(\tilde{\boldsymbol{\Lambda}})$$
其中$\tilde{\boldsymbol{\Lambda}}=\frac{2}{\lambda_{max}}\boldsymbol{\Lambda}-\boldsymbol{I}_n$,$\lambda _{max}$ 是矩陣$L$的最大特徵值(譜半徑)。再利用切比雪夫多項式遞推公式:
$$T_k(x)=2xT_{k-1}(x)-T_{k-2}(x)$$
$$T_0(x)=1,T_1(x)=x$$
所以有因為$L^{j}x$,那麼
$$\begin{aligned} \boldsymbol{g(\wedge )}_{\boldsymbol{\theta^{\prime}}} * \boldsymbol{x} &\approx \boldsymbol{U} \sum_{k=0}^K \theta_k^{\prime} T_k(\tilde{\boldsymbol{\Lambda}}) \boldsymbol{U}^T \boldsymbol{x} \ \\ &= \sum_{k=0}^K \theta_k^{\prime} (\boldsymbol{U} T_k(\tilde{\boldsymbol{\Lambda}}) \boldsymbol{U}^T) \boldsymbol{x} \\ &=\sum_{k=0}^K \theta_k^{\prime} T_k(\tilde{\boldsymbol{L}}) \boldsymbol{x} \end{aligned}$$
其中$\tilde{\boldsymbol{L}}=\frac{2}{\lambda_{max}} \boldsymbol{L}- \boldsymbol{I}_n$
所以有$$\boldsymbol{y}_{output} = \sigma(\sum_{k=0}^K \theta_k^{\prime} T_k(\tilde{\boldsymbol{L}}) \boldsymbol{x})$$
改進二
主要對上式做了簡化處理,取 $K=1$,設定$\lambda_{max}\approx 2$,帶入簡化模型:
$$\begin{aligned} \boldsymbol{g}_{\boldsymbol{\theta^{\prime}}} * \boldsymbol{x} &\approx \theta_0^{\prime} \boldsymbol{x} + \theta_1^{\prime}(\boldsymbol{L}- \boldsymbol{I}_n) \boldsymbol{x} \\ &= \theta_0^{\prime} \boldsymbol{x} - \theta_1^{\prime}(\boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2}) \boldsymbol{x} \end{aligned}$$
上述用到了歸一化的拉普拉斯矩陣,$$\boldsymbol{L}=\boldsymbol{D}^{-1/2}(\boldsymbol{D}-\boldsymbol{W})\boldsymbol{D}^{-1/2}=\boldsymbol{I_n}-\boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2}$$
進一步假設$\theta_0^{\prime}=-\theta_1^{\prime}$
$$\boldsymbol{g}_{\boldsymbol{\theta^{\prime}}} * \boldsymbol{x} = \theta(\boldsymbol{I_n} + \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2}) \boldsymbol{x}$$
但是考慮到$\boldsymbol{I_n} + \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2}$的特徵值範圍是$[0, 2]$,會引起梯度消失問題(這點暫不清楚why),所以再修改為:
$$\boldsymbol{I_n} + \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2} \rightarrow \tilde{\boldsymbol{D}}^{-1/2}\tilde{\boldsymbol{W}} \tilde{\boldsymbol{D}}^{-1/2}$$
$\tilde{\boldsymbol{W}}=\boldsymbol{W}+\boldsymbol{I}_n$ 相當於鄰接矩陣中對叫上加了$1$
最後就是論文中提到的形式:
$$\boldsymbol{Z}_{\mathbb{R}^{N \times F}} = (\tilde{\boldsymbol{D}}^{-1/2}\tilde{\boldsymbol{W}} \tilde{\boldsymbol{D}}^{-1/2})_{\mathbb{R}^{N \times N}} \boldsymbol{X}_{\mathbb{R}^{N \times C}} \ \ \boldsymbol{\Theta}_{\mathbb{R}^{C \times F}}$$
GCN定義
簡單來說,網路的輸入是$\mathcal{G}=(\mathcal{V}, \mathcal{E})$,可以得到$N\times D$的輸入矩陣$X$($N$個頂點,每個結點$D$維),和鄰接矩陣$A$,一層的輸出是$Z$($N\times F$,F是輸出結點的維度),其中每一層可以寫成一個非線性函式:

一種簡單的形式
直覺來說如果沒有上文複雜的$ (\tilde{\boldsymbol{D}}^{-1/2}\tilde{\boldsymbol{W}} \tilde{\boldsymbol{D}}^{-1/2})_{\mathbb{R}^{N \times N}}$ 推導,那麼我們會設計成如下形式,$A$為鄰接矩陣,$H^{(l)}$為結點再$l$層的特徵表示。

這種設計一個明顯可以提到的地方就是$A$矩陣對角為0(導致每下一層丟失了自己的資訊),所以可以改進為,$\tilde{A}=A+I$。還有一個不好的是,沒有歸一化$A$,會出現對$W$求導的時候,$A$的元素≥1,有梯度消失的隱患——那麼就做一個歸一化咯,得到$D^{-1}A$,(我覺得可以了),但是作者說:dynamics get more interesting when we use a symmetric normalization——所以使用了$D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$的歸一化形式。【$D^{-1}A$當然不等同於$D^{-1/2}AD^{-1/2}$,不要被兩個$-1/2$就是$-1$迷惑。是容易驗證的】
所以,直覺上,有了:$$f(H^{(l)}, A) = \sigma\left( \hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) \, $$
但是理論的推導其實是從上文大篇幅的介紹而來的。
參考文獻:
https://www.zhihu.com/question/54504471
http://tkipf.github.io/graph-convolutional-networks/
https://www.davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/#
https://arxiv.org/abs/1609.0
