目錄

• Node Embedding
• Random Walk
• node2vec
• TransE
• Embedding Entire Graph
  • Anonymous Walk
• Reference

轉自本人：https://blog.csdn.net/New2World/article/details/105536633

Node Embedding

上一講介紹了對圖中節點進行分類的方法，涉及了節點自身的特徵以及圖的結構資訊。然而當特徵這個概念出現就說明需要做特徵工程，這是相當費時費力的工作。最後的結果還不一定理想，因為或多或少會丟失一些資訊。因此我們希望能讓演算法自己學習節點特徵，雖然這樣的到的特徵向量並不像傳統意義上的特徵那樣每一列有明確的意義，而更有一種對節點進行編碼(embedding)的味道。其中最簡單的例子就是 one-hot，但這種簡單 embedding 的方式存在很多問題，比如泛化性差，維度高，資訊缺失等。因此我們希望得到的 embedding 有一些很好的性質，比如 embedding 的相似度能反映節點在網路中的相似度。這裡的相似度是根據不同應用場景進行定義的，可以是拓撲結構上的相鄰，也可以是之前提到的相同的角色。embedding 的相似度計算也需要針對不用應用場景或需求來定義，但一般情況下采用的還是向量的內積。
有了這個大體思路我們就可以將這個學習節點 embedding 的過程簡單分為 3 步：

1. 定義一個編碼器
2. 定義節點的相似度
3. 對編碼器的引數進行優化，使得 \(similarity(u,v)\approx z_v^Tz_u\)

Random Walk

隨機遊走，正如這個名字描述的那樣，節點從一個點開始沿著圖中的邊“亂”跑，途經的節點的 multiset(節點可重複) 就是我們想要的東西。為什麼我們要這種看似無章可循的“亂”生成的結果？這其實是定義節點相似度的一種方法。假設現在我們需要節點 \(u\) 的 embedding，且我們希望節點相似度定義為結構上較為接近的點具有更高相似度。那最容易想到的方法就是鄰接節點，這些點的相似度一定很高，這要能最大化這一部分點的 embedding 相似度就好了。想法很好也很正確，但是這樣做存在兩個問題。首先，如果只找鄰接節點，那獲得的資訊就只有 \(1\) hop，這樣得到的結果太侷限了。再說直觀上也說不通，就好比和節點 \(u\) 直接相連的節點和 \(u\) 很類似，而 \(u\) 鄰接點的鄰接點就和 \(u\) 完全沒有關係了。那可能就有人說，大不了我多迭代幾次，考慮跑個 \(k\) hop。那麼這就涉及到第二個問題，對於大規模的網路一部分節點的度很高，例如微軟 MSN 的網路最高的度是指數級別的，因此找所有鄰接節點代價太高更別說還要找鄰接點的鄰接點了。
這麼一來，這個隨機遊走看起來是不是就很漂亮了。首先它隨機傳播，只要我們控制好傳播距離就能實現多 hop。其次它不要求遍歷所有鄰接點，但只要隨機次數足夠它還是能覆蓋大部分鄰接點。
然後根據隨機遊走的結果來定義相似度就很簡單了，即節點 \(u\) 和 \(v\) 的 embedding 相似度和這兩個節點同時出現在隨機遊走的結果中的概率成正比。你細品是不是這個道理。
有了相似度，接下來就是優化的過程。我們用 log-likelihood 來做。這裡將隨機遊走的結果記為 \(N_R(u)\)

\[\begin{aligned} \min L&=-\sum_{u\in v}\log P(N_R(u)|z_u) \\ &=\sum_{u\in V}\sum_{v\in N_R(u)}-\log P(v|z_u) \end{aligned}\]

然後因為是概率，所以我們用 softmax 來定義 \(P(v|z_u)\)

\[P(v|z_u)=\frac{\exp(z_u^Tz_v)}{\sum_{n\in V}\exp(z_u^Tz_n)} \]

為什麼是 softmax ？
因為 \(\sum_i\exp(x_i)\approx\max_i\exp(x_i)\)

然而就算 numpy 再方便再快也經不起套娃的 sum 那 \(O(|V|^2)\) 的複雜度呀。於是採用了 negative sampling 的方法取代每次計算所有節點相似度和的步驟。negative sampling 說白了就是從所有節點中按照分佈 \(P_V\) 隨機選點。在這個場景下，每個點被選中的概率和它自身的 degree 成正比。

\[\log(\frac{\exp(z_u^Tz_v)}{\sum_{n\in V}\exp(z_u^Tz_n)})\approx\log\sigma(z_u^Tz_v)-\sum\limits_{i=1}^k\log\sigma(z_u^Tz_{n_i}) \]

隨機選一些點不是會損失很多精度嗎？看起來是的，但實際上這樣做沒什麼問題。為什麼？這個過程很複雜，有空我再去看，paper 連結先放這兒 https://arxiv.org/pdf/1402.3722.pdf
這裡的 \(k\) 是 negative sampling 選點的超引數，一般來說 \(k\) 取 \(5\)~\(20\)。太高的 \(k\) 雖然能得到更穩定的結果，但 bias 會增加，因為選點概率和度成正比。

node2vec

上面提到的這種是長度固定的無偏隨機遊走。它的約束太強了導致得到的 embedding 泛化能力有限。這也是一個很重要的點，即更寬鬆的約束條件下得到的 embedding 更豐富。接下來介紹的這個也是隨機遊走，但它的規則不一樣。slide 裡介紹的這是一個有偏的二階隨機遊走，有偏會在下面介紹，但這裡我是沒看出來哪裡體現了二階。
node2vec 裡有兩個關鍵超引數，return \(p\) 和 in-out \(q\)。下圖很直觀地展示了這兩個引數的用途。首先從 \(s_1\) 出發到達 \(w\) 後需要決定下一步走哪裡，我們按 \(1/p\) 的相對概率回到 \(s_1\)，\(1\) 的相對概率進行 BFS 即 \(s_1\) 的下一個鄰接節點，或者按 \(1/q\) 的相對概率傳播出去即 DFS。如此一來就能 capture 到區域性和全域性特徵了。這種方法在節點分類任務裡效果很好。
注意，這裡並不是概率，而是相對概率關係。

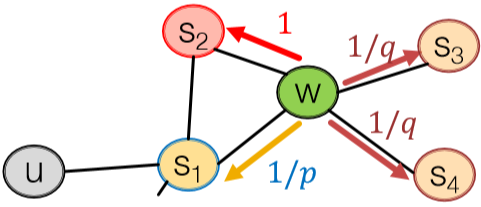
接下來就是用 SGD 做優化了。

TransE

TransE 其實也是一個學習節點 embedding 的演算法。我對這個演算法比較感興趣，因為我一直想涉足知識圖譜領域，而且我本科導師帶的研究生就在做 TransE 相關的東西，我也或多或少了解過一點它的神奇特性。比如現在我們的圖譜裡有幾個實體：“北京”，“中國”，“華盛頓”，“美國”；同時還有關係：“中國”\(\rightarrow\)“北京”，“美國”\(\rightarrow\)“華盛頓”。顯而易見這個關係其實是“首都”的含義，那麼 TransE 能做到 “中國” - “北京” = “美國” - “華盛頓” = “首都” (當然，其實並沒有“首都”這麼一個實體，只是方便解釋)。而這一特性就能完成 link prediction 的任務。比如我現在有“巴黎”和“法國”但沒有這兩個實體見的關係，那我們可以做的就是計算出 “法國” - “首都” 然後計算得到的結果和其它城市實體的相似度，而最終會發現“巴黎”的相似度最高。
之所以 TransE 能做到這一點，跟它的計算方式有關。它並非採用的隨機遊走的方法，而是採用上面說到的這種特性來做的優化。首先將實體和關係定義為三元組 \((h,l,t)\)，分別表示頭實體、關係和尾實體 (有向)。然後

由此可見，隨機遊走並不是生成節點 embedding 的唯一方法，條條大路通羅馬。

Embedding Entire Graph

最後一部分對整個圖做 embedding 講得很匆忙，我之前也沒有太多關心過這個問題。不過根據 slide 自己理解了下。大致有三種方法

1. 暴力求和
2. 虛擬點表示圖或子圖，然後用標準的 embedding 方法來做。參考 Li et al., 2016
3. Anonymous walk

Anonymous Walk

這個玩意兒很神奇。它的定義和國內小學語文題類似，比如寫出形如 AABB 的詞語。但是這樣的話有個疑惑，圖中的 ABCDE 是怎麼標的？事先有標籤？還是怎麼做？不是無監督學習嗎？這需要看看論文再回來解決。

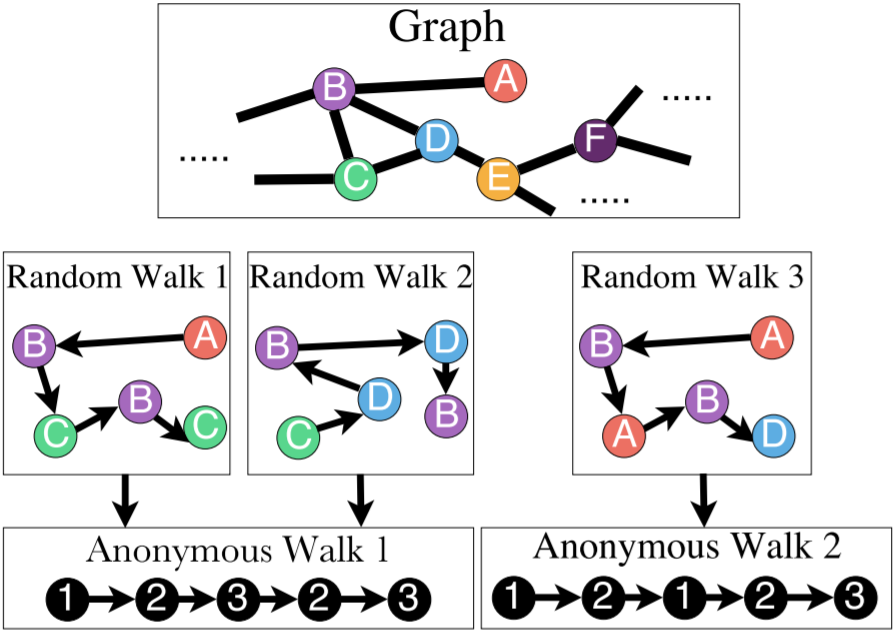
利用 anon. walk 也有幾種方法來 embed 整個圖。

第一種方法，我們先枚舉出長度為 \(l\) 的所有 anon. walk，然後將圖的 embedding 表示為這些遊走的概率分佈。比如長度為 \(3\) 的話就有 \(5\) 中排列，那麼圖的 embedding 就是一個 5D 向量。

第二種方法，我們生成 \(m\) 個隨機遊走的結果，然後根據這個結果計算經驗分佈。而這個 \(m\) 的取值是有下界的，我們希望誤差大於 \(\varepsilon\) 的概率小於 \(\delta\) 的話

\[m=\lceil\frac2{\varepsilon^2}(\log(2^\eta-2)-\log(\delta)\rceil \]

其中 \(\eta\) 是長度為 \(l\) 的 anon. walk 的個數。

第三種方法，既然是機器學習那何不連遊走過程一起學了？這裡的 idea 是希望能編碼遊走過程使得下一個遊走能被預測，即 \(P(w_t^u|w_{t-\Delta}^u,...,w_{t-1}^u)\) 這裡的 \(w_t^u\) 是從節點 \(u\) 出發的第 \(t\) 個隨機遊走。

1. 從節點 \(u\) 開始跑 \(T\) 次 Rnd walk 得到 \(N_R(u)=\{w_1^u,w_2^u,...,w_T^u\}\)
2. 然後給定長度為 \(Delta\) 的滑窗，讓演算法學著預測在滑窗內同時出現的 walk

\[\begin{aligned} \max\frac1T\sum\limits_{t=\Delta}^T\log P(w_t|w_{t-\Delta},...,w_{t-1}) \\ P(w_t|w_{t-\Delta},...,w_{t-1})=\frac{\exp(y(w_t))}{\sum_i^n\exp(y(w_i))} \\ y(w_t)=b+U(\frac1{\Delta}\sum\limits_{i=1}^{\Delta}z_i) \end{aligned}\]

這裡 \(b\in\R\)，\(U\in\R^D\)，\(z_i\) 是 anon. walk 的 embedding。詳細參考 Anonymous Walk Embeddings, ICML 2018

Reference

[1]: 這兒有一篇關於各種 embedding 方法的 survey：Goyal and Ferrara, 2