[toc] 轉自本人：[https://blog.csdn.net/New2World/article/details/106265878](https://blog.csdn.net/New2World/article/details/106265878) 我們研究網路，不僅是為了提取網路結構的特徵或對節點進行分類。更多的是為了研究網路上的傳播過程，比如訊息在社交網路中的傳播，以及傳染病在人群中的傳播。而現實世界中的網路是不會顯式地表現出傳播過程的，而是通過時間先後的關係展示出傳播性的。 ## Decision Based Model of Diffusion 現在有兩種選擇 A 和 B，一個人現在要決定要麼選 A 要麼選 B。如果你的朋友和你做出同樣的選擇那麼能得到一定的獎勵，否則沒有獎勵。就像分系統的手遊，你用 IOS 你可以和你周圍用 IOS 的朋友一起玩，開心；但這樣就失去了 Android 的朋友。那麼用數學來描述就是，選 A 能得到 a 的 payoff，B 能得到 b。然後你有 d 個朋友，他們之中選擇 A 的佔比例 p，那麼 $$payoff = \begin{cases}a\cdot p\cdot d\ \ \ \ choose A\\ b\cdot (1-p)\cdot d\end{cases}\ \ \ \ choose B$$ 其實通過 a 和 b 的大小就能判斷出為了將利益最大化是應該選 A 還是選 B。先定義一個閾值 $q = \frac b{a+b}$，如果 p 大於這個閾值就說明選擇 A 更有利，而當小於閾值時選擇 B 得到的回報更多。那麼為了簡化問題，我們假設 $a = b-\epsilon$ 即 a b 基本相等，且 $q = 1/2$。這就變成了一個“從眾”的問題了，即選哪個的人多我選哪個。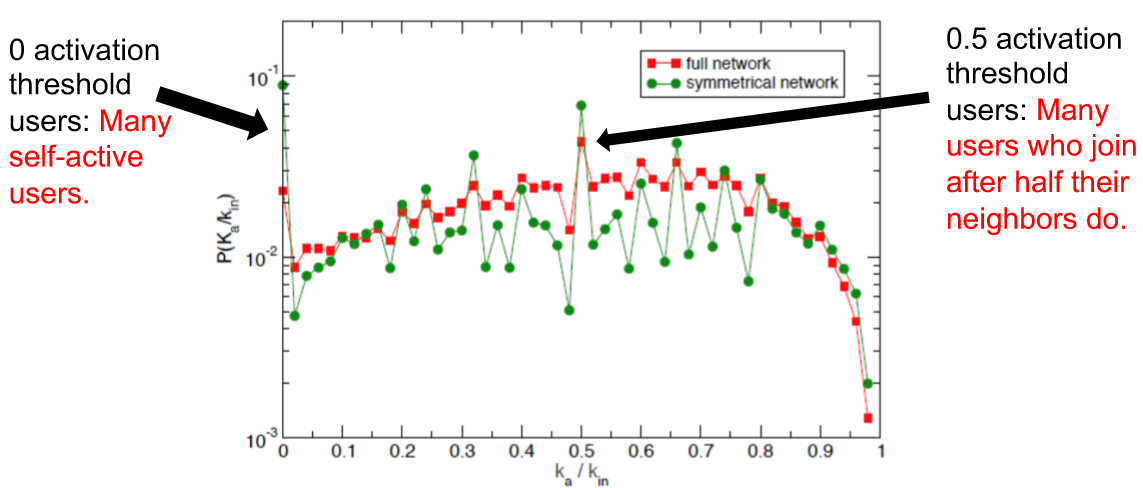 這裡選擇了 2011 年 Twitter 上西班牙在經濟危機期間爆發的大規模抗議的話題為例。對使用了對應話題的 hashtag 的使用者及使用者間關係進行分析。定義兩個符號 $k_{in}$ 表示當一個使用者開始參加抗議活動時他有多少好友，以及 $k_a$ 此刻他有多少已經參加抗議了的朋友。然後將兩個值的比定義為 activation threshold $k_a/k_{in}$ 表示參加抗議的朋友佔多大比例的時候，一個人可能會跟著一起參加。如果這個閾值趨近 $0$ 說明他可能是發起者之一；而如果趨近 $1$ 說明他受到了很大的“社會壓力”，可能是“被迫”參加的抗議。下面這張圖能看出很多人在超過半數的朋友參加後參加的，也有很多人是自發參加的。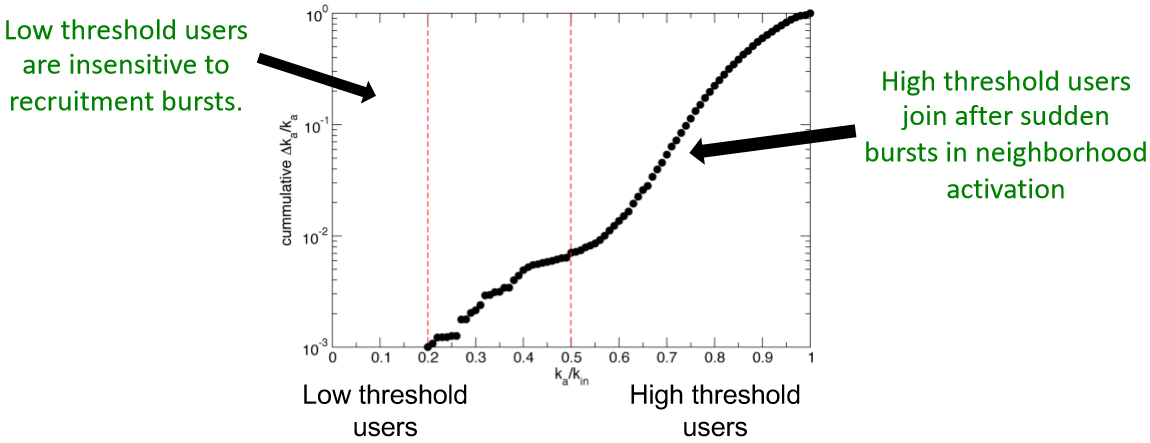  另一個假說是當很多朋友在短時間內都參加了抗議那這個使用者大概率也會參加。而下面這個圖有印證了這一點。注意縱座標是累計的 $\Delta k_a/k_a=(k_a^{t+1}-k_a^t)/k_a^{t+1}$，也就是說圖中曲線上升快則表示短時間加入的人多。  ### Large Cascades 一個規律：規模很大的、“成功的” cascade 其實很少，大部分 cascade 都是中小規模的，那這些“成功的” cascade 是有誰或者哪一些人發起的呢？引入一種研究方法：k-core decomposition。所有節點都有至少 k 個 degree 的最大連通子圖。如下圖所示，k 越大說明這些節點更挨近“中心位置”。而大規模的 cascade 一般由這些靠近中心的節點發起。這種方法相比於 degree distribution 的優點是它能告訴我們哪些節點很有“影響力”的且相互連線。  ## Extending the Model 上面的模型只考慮了單選，如果一個個體能同時選擇兩個呢？比如我既買 IOS 也買 Android，那我既能跟 IOS 的好友玩也能跟 Android 的朋友玩，豈不美哉。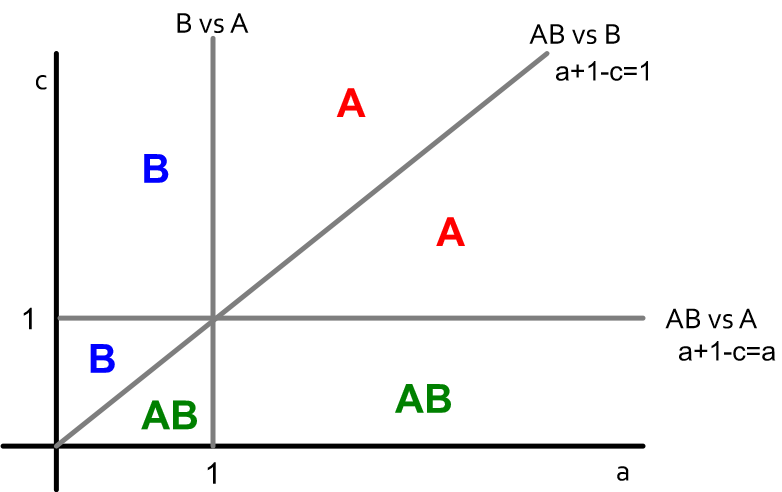然而，這樣的話我得付出一定“代價” c，即我得買倆手機，氪兩份金…… 還是用符號來表示的話就是 - AB - A / A - A: gets a - AB - B / B - B: gets b - AB - AB: gets $max(a,b)-c$ 簡化我們的網路結構，針對一條鏈進行分析。假如我們要確定中間節點的決策，那現在就有兩種需要討論的情況：(為了方便，設 $b=1$) 1. 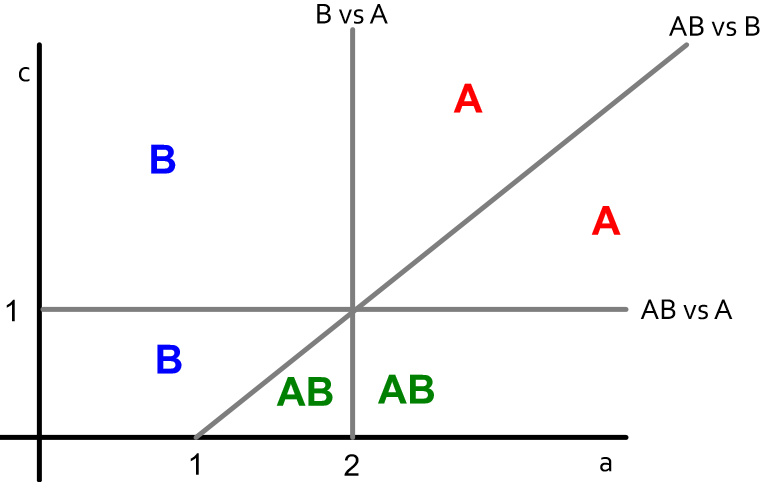兩邊的相鄰節點為不同的單一選擇，那麼中間節點的選擇對應的回報是：A - a, B - 1, AB - a+1-c  2. 其中一邊為多選，另一邊單選，那中間節點的選擇：A - a, B - 1+1, AB - max(a,1)+1-c  ## Probabilistic Spreading Models 上面講了基於決策的模型，但現實生活中有些事情並不是人們的意願能控制的，比如疾病傳播。並不是說一個人過半數的朋友沒被傳染這個人就很安全，也並不是說當你的人際關係中半數以上的朋友感染了你就一定會感染，這只是概率大小的問題。 假設一個病人平均和 $d$ 個人接觸過，並且以概率 $q>0$ 傳染給其他人。那我們要研究的是當 $d$ 和 $q$ 取什麼值或者滿足什麼條件的時候，這個病毒會持續傳播直到感染所有人。如果將病毒傳播看成一棵樹，那麼從0號病人開始向下展開，樹的每一層就是一代感染/傳播者，那麼上述問題就轉換為了在 $d$ $q$ 滿足什麼條件的情況下 $$\lim_{h\rightarrow\infty} P[a\ node\ at\ depth\ h\ is\ infected]\begin{cases} > 0,\ \ \ \ run\ forever \\= 0,\ \ \ \ die\ out\end{cases}$$ 對於深度為 $h$ 的節點，不被感染的概率為 $(1-q\cdot p_{h-1})^d$，即 $h-1$ 的節點不傳染給他接觸的 $d$ 個人中的任意一個。那麼反過來 $1-(1-q\cdot p_{h-1})^d$ 就是深度為 $h$ 的節點存在被感染的概率。寫成迭代的形式就是 $f(x) = 1-(1-q\cdot x)^d$。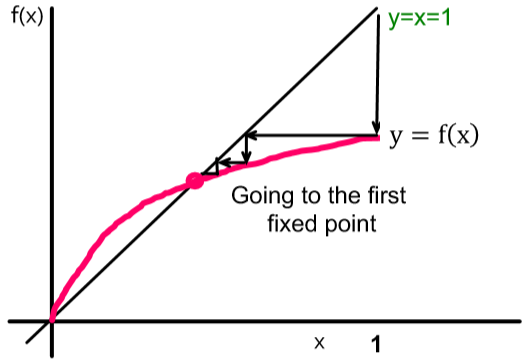  因為 x 的初始值為 1，即0號病人，那麼接下來函式 $f(x)$ 的一系列變化可以從上圖中直觀看出來是個向左遞減的過程。而這條曲線和 $f(x) = x$ 這條線的交點代表從某一深度開始節點被感染的概率都相等且為一個固定值了。 > 這張圖如果視為函式影象的話是沒有問題的；但作為這裡的傳播概率的話，從 $x=1$ 到 $f(x)=x$ 的 fixed point 之後就不會再往左畫了，即曲線只存在於 $f(x)=x$ 下面。 那麼我們想讓這個傳播在一定深度後 die out，就是讓這個 fixed point 落在原點上。通過分析梯度不難發現整個函式是單增的，但其梯度是單調非遞增的，即函式增加趨勢漸弱。於是考慮 $f(\cdot)$ 在原點的梯度為 $f'(0)=q\cdot d$，因此只要 $f'(0) < 1$ 就能保證這個 fixed point 在原點上。這就是傳染病學中判斷病毒傳播能力的 $R_0$ 值，它的物理意義也很直觀：$q\cdot d$ 表示一個人平均能傳染多少人。如果 $R_0 \geq 1$ 則說明每個患者至少能傳染一個人，那到最後全世界的人都可能被傳染；但如果 $R_0 < 1$ 則表示病毒可能不會傳染任何一個人，這樣一來可能到最後病毒就消失了。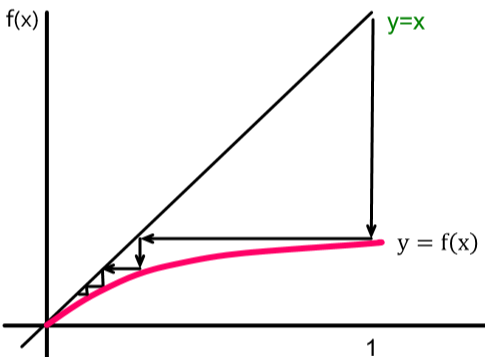  因此控制傳染病的有效手段主要有 1. 降低 $d$：採取隔離措施，減少人與人之間的接觸 2. 降低 $q$：勤洗手，戴口罩 這裡給出了一些傳染病的 $R_0$ 值 1. HIV：2~5 2. 麻疹：12~18 3. 埃博拉：1.5~2 傳染病的傳播能力還受很多因素影響，比如埃博拉的 $R_0$ 看似不高，實則是因為其高死亡率導致病毒傳播效率低。因此 $R_0$ 只是一個作為參考的數值。 然後就有研究者通過對 Flickr 上圖片的點贊來驗證 $R_0$ 值對社交網路的有效性。他們通過 $q\cdot d\cdot \frac{avg(d_i^2)}{(avg d_i)^2}$ (後面的分式是為了矯正度分佈的偏度而加入的) 作為 $R_0$ 的估計值，然後根據時間先後關係對每個使用者點贊圖片的情況直接數他影響到的使用者個數來作為參照。這樣得到的結果的相關係數為 $0.9765$，說明符合度較高。而 $R_0$ 在 1 到 190 間，說明社交網路上的媒體傳播效率相當之高。 ## Epidemic Models 病毒傳播的兩個重要引數 1. birth rate $\beta$：受感染者傳播給未受感染者的概率 2. 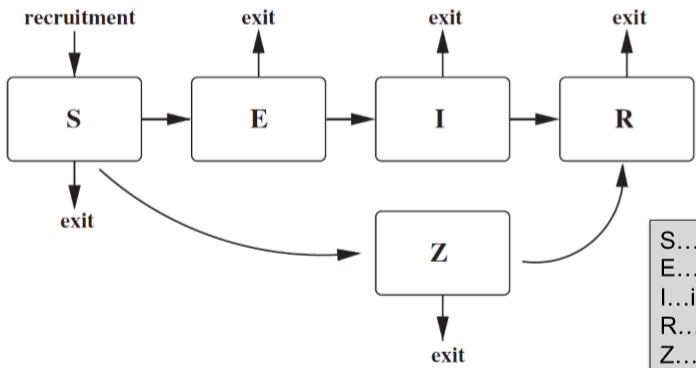death rate $\delta$：受感染者治癒的概率 然後一般遵循 SEIRZ 的模式，即 - S: susceptible - E: exposed - I: infected - R: recovered - Z: immune  這個模型可以只取一部分，比如水痘的模型就是 SIR，即一旦治癒就不會再長水痘。那麼這個模型的動態可以表示為 $$\frac{dS}{dt}=-\beta SI \\ \frac{dR}{dt}=\delta I \\ \frac{dI}{dt}=\beta SI-\delta I$$ 這裡的微分表示對應部分個體數變化速率，不過我沒搞懂為什麼 dS 這裡要乘 I ？ 另一種模型是 SIS，即被治癒的個體有再一次被感染的風險 $$\frac{dS}{dt}=-\beta SI+\delta I \\ \frac{dI}{dt}=\beta SI-\delta I$$ 此時病毒的 strength 為 $\beta / \delta$，且存在一個閾值 $\tau$，如果病毒的感染能力 $\beta / \delta < \tau$，表明這個病毒最終會消失。那這個閾值如何確定？$\tau=1/\lambda_{1,A}$，其中 $\lambda_{1,A}$ 是圖的鄰接矩陣的最大特徵值[^1]。事實表明，這個病毒是否消失與最初有多少人感染無關。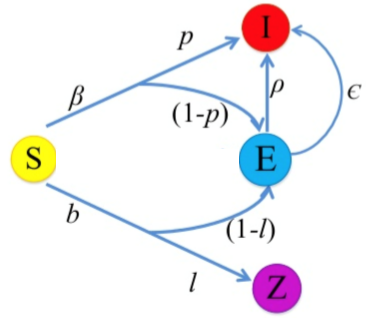 ### Rumor spread modeling using SEIZ 用 SEIZ 分析 twitter 上的謠言 - S: Twitter 賬號 - I: 相信事實 / 謠言，並轉發 - E: 還沒相信 - Z: 質疑，還沒轉發  上圖詳細地描述了各個狀態間的轉移概率。然後通過網格搜尋最小化 $|I(t)-tweets(t)|$ 來訓練模型。具體怎麼訓練……超綱了沒講，有空我去看看，隨緣補充……下圖中的 ODE 是常微分方程。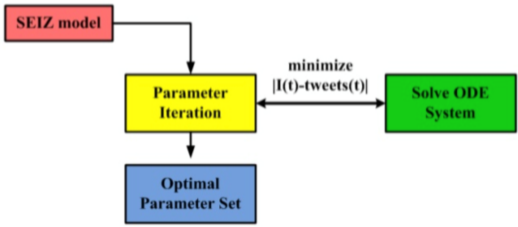  將 SEIZ 用在社交網路上的話，會使用一種新的指標來評估傳播效率 $$R_{SI}=\frac{(1-p)\beta+(1-l)b}{\rho+\epsilon}$$ 這個指標是一種 flux ratio，即通量比。它標明瞭“進入狀態 E 和離開狀態 E 的資料量的比值”。也就是說，$R_{SI}$ 越低說明看到謠言的人多同時轉發的人也多，即傳播效率很高；反之，謠言不流行。 而實驗結果顯示，謠言的接受率驚人地高，可見“愚昧”的人不少，也可能是這些謠言的包裝真的厲害。 [^1]: 為什麼鄰接矩陣的最大特徵值的倒數是閾值？難道它揭示了網路的疏密