《機器學習_07_03_svm_核函式與非線性支援向量機》
阿新 • • 發佈:2020-05-22
### 一.簡介
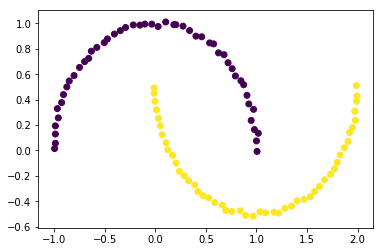
前兩節分別實現了硬間隔支援向量機與軟間隔支援向量機,它們本質上都是線性分類器,只是軟間隔對“異常點”更加寬容,它們對形如如下的螺旋資料都沒法進行良好分類,因為沒法找到一個直線(超平面)能將其分隔開,必須使用曲線(超曲面)才能將其分隔,而核技巧便是處理這類問題的一種常用手段。
```python
import numpy as np
import matplotlib.pyplot as plt
import copy
import random
import os
os.chdir('../')
from ml_models import utils
from ml_models.svm import *
from sklearn import datasets
%matplotlib inline
```
```python
data, target = datasets.make_moons(noise=0.01)
plt.scatter(data[:,0],data[:,1],c=target)
plt.show()
```
### 二.核技巧
核技巧簡單來說分為兩步:
(1)將低維非線性可分資料$x$,通過一個非線性對映函式$\phi$,對映到一個新空間(高維度甚至是無限維空間);
(2)對新空間的資料$\phi(x)$訓練線性分類器
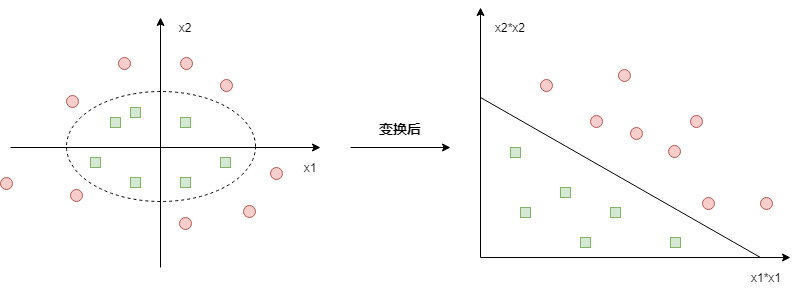
比如如下的情況:
原始資料需要使用一個橢圓才能分隔開,但對原始資料施加一個非線性變換$\phi:(x_1,x_2)->(x_1^2,x_2^2)$變換後,在新空間中就可以線性分隔了
 #### 利用核技巧後的SVM
所以,如果對原始資料施加一個對映,此時軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_i\phi(x_i)^T\phi(x)+b^*)
$$
### 三.核函式
觀察一下上面公式,我們的目的其實是求解$\phi(x_i)^T\phi(x_j)$,有沒有一種函式讓$(x_i,x_j)$只在原始空間做計算就達到$\phi(x_i)^T\phi(x_j)$的效果呢?有的,那就是核函式,即:
$$
K(x_i,x_j)=\phi(x_i)^T\phi(x_j)
$$
#### 怎樣的函式才能做核函式?
要成為核函式必須滿足如下兩點條件:
(1)對稱性:$K(x_i,x_j)=K(x_j,x_i)$
(2)正定性:對任意的$x_i,i=1,2,..,m$,$K(x,z)$對應的Gramm矩陣:
$$
K=[K(x_i,x_j)]_{m\times m}
$$
是半正定矩陣,這裡的$x_i\in$可行域,並不要求一定要屬於樣本集
#### 常見的核函式有哪些?
目前用的比較多的核函式有如下一些:
(1)多項式核函式:
$$
K(x,z)=(x^Tz+1)^p
$$
(2)高斯核函式:
$$
K(x,z)=exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})
$$
顯然,線性可分SVM中使用的是$K(x,z)=x^Tz$也是核函式
#### 利用核函式後的SVM
利用核函式後,軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_iK(x,x_i)+b^*)
$$
### 四.程式碼實現
程式碼實現很簡單,就在軟間隔SVM的基礎上將向量的內積計算$x^Tz$替換為$K(x,z)$即可,首先定義一些核函式:
```python
"""
該部分放到ml_model.kernel_functions中
"""
def linear():
"""
線性核函式
:return:linear function
"""
def _linear(x, y):
return np.dot(x, y)
return _linear
def poly(p=2):
"""
多項式核函式
:param p:
:return: poly function
"""
def _poly(x, y):
return np.power(np.dot(x, y) + 1, p)
return _poly
def rbf(sigma=0.1):
"""
徑向基/高斯核函式
:param sigma:
:return:
"""
def _rbf(x, y):
np_x = np.asarray(x)
if np_x.ndim <= 1:
return np.exp((-1 * np.dot(x - y, x - y) / (2 * sigma * sigma)))
else:
return np.exp((-1 * np.multiply(x - y, x - y).sum(axis=1) / (2 * sigma * sigma)))
return _rbf
```
```python
from ml_models import kernel_functions
class SVC(object):
def __init__(self, epochs=100, C=1.0, tol=1e-3, kernel=None, degree=3, gamma=0.1):
"""
:param epochs: 迭代次數上限
:param C: C越小,對於誤分類的懲罰越小
:param tol:提前中止訓練時的誤差值上限,避免迭代太久
:param kernel:核函式
:param degree:kernel='poly'時生效
:param gamma:kernel='rbf'時生效
"""
self.b = None
self.alpha = None
self.E = None
self.epochs = epochs
self.C = C
self.tol = tol
# 定義核函式
if kernel is None:
self.kernel_function = kernel_functions.linear()
elif kernel == 'poly':
self.kernel_function = kernel_functions.poly(degree)
elif kernel == 'rbf':
self.kernel_function = kernel_functions.rbf(gamma)
else:
self.kernel_function = kernel_functions.linear()
# 記錄支援向量
self.support_vectors = None
# 記錄支援向量的x
self.support_vector_x = []
# 記錄支援向量的y
self.support_vector_y = []
# 記錄支援向量的alpha
self.support_vector_alpha = []
def f(self, x):
"""
:param x:
:return: wx+b
"""
x_np = np.asarray(x)
if len(self.support_vector_x) == 0:
if x_np.ndim <= 1:
return 0
else:
return np.zeros((x_np.shape[:-1]))
else:
if x_np.ndim <= 1:
wx = 0
else:
wx = np.zeros((x_np.shape[:-1]))
for i in range(0, len(self.support_vector_x)):
wx += self.kernel_function(x, self.support_vector_x[i]) * self.support_vector_alpha[i] * \
self.support_vector_y[i]
return wx + self.b
def init_params(self, X, y):
"""
:param X: (n_samples,n_features)
:param y: (n_samples,) y_i\in\{0,1\}
:return:
"""
n_samples, n_features = X.shape
self.b = .0
self.alpha = np.zeros(n_samples)
self.E = np.zeros(n_samples)
# 初始化E
for i in range(0, n_samples):
self.E[i] = self.f(X[i, :]) - y[i]
def _select_j(self, best_i):
"""
選擇j
:param best_i:
:return:
"""
valid_j_list = [i for i in range(0, len(self.alpha)) if self.alpha[i] > 0 and i != best_i]
best_j = -1
# 優先選擇使得|E_i-E_j|最大的j
if len(valid_j_list) > 0:
max_e = 0
for j in valid_j_list:
current_e = np.abs(self.E[best_i] - self.E[j])
if current_e > max_e:
best_j = j
max_e = current_e
else:
# 隨機選擇
l = list(range(len(self.alpha)))
seq = l[: best_i] + l[best_i + 1:]
best_j = random.choice(seq)
return best_j
def _meet_kkt(self, x_i, y_i, alpha_i):
"""
判斷是否滿足KKT條件
:param w:
:param b:
:param x_i:
:param y_i:
:return:
"""
if alpha_i < self.C:
return y_i * self.f(x_i) >= 1 - self.tol
else:
return y_i * self.f(x_i) <= 1 + self.tol
def fit(self, X, y2, show_train_process=False):
"""
:param X:
:param y2:
:param show_train_process: 顯示訓練過程
:return:
"""
y = copy.deepcopy(y2)
y[y == 0] = -1
# 初始化引數
self.init_params(X, y)
for _ in range(0, self.epochs):
if_all_match_kkt = True
for i in range(0, len(self.alpha)):
x_i = X[i, :]
y_i = y[i]
alpha_i_old = self.alpha[i]
E_i_old = self.E[i]
# 外層迴圈:選擇違反KKT條件的點i
if not self._meet_kkt(x_i, y_i, alpha_i_old):
if_all_match_kkt = False
# 內層迴圈,選擇使|Ei-Ej|最大的點j
best_j = self._select_j(i)
alpha_j_old = self.alpha[best_j]
x_j = X[best_j, :]
y_j = y[best_j]
E_j_old = self.E[best_j]
# 進行更新
# 1.首先獲取無裁剪的最優alpha_2
eta = self.kernel_function(x_i, x_i) + self.kernel_function(x_j, x_j) - 2.0 * self.kernel_function(
x_i, x_j)
# 如果x_i和x_j很接近,則跳過
if eta < 1e-3:
continue
alpha_j_unc = alpha_j_old + y_j * (E_i_old - E_j_old) / eta
# 2.裁剪並得到new alpha_2
if y_i == y_j:
L = max(0., alpha_i_old + alpha_j_old - self.C)
H = min(self.C, alpha_i_old + alpha_j_old)
else:
L = max(0, alpha_j_old - alpha_i_old)
H = min(self.C, self.C + alpha_j_old - alpha_i_old)
if alpha_j_unc < L:
alpha_j_new = L
elif alpha_j_unc > H:
alpha_j_new = H
else:
alpha_j_new = alpha_j_unc
# 如果變化不夠大則跳過
if np.abs(alpha_j_new - alpha_j_old) < 1e-5:
continue
# 3.得到alpha_1_new
alpha_i_new = alpha_i_old + y_i * y_j * (alpha_j_old - alpha_j_new)
# 5.更新alpha_1,alpha_2
self.alpha[i] = alpha_i_new
self.alpha[best_j] = alpha_j_new
# 6.更新b
b_i_new = y_i - self.f(x_i) + self.b
b_j_new = y_j - self.f(x_j) + self.b
if self.C > alpha_i_new > 0:
self.b = b_i_new
elif self.C > alpha_j_new > 0:
self.b = b_j_new
else:
self.b = (b_i_new + b_j_new) / 2.0
# 7.更新E
for k in range(0, len(self.E)):
self.E[k] = self.f(X[k, :]) - y[k]
# 8.更新支援向量相關的資訊
self.support_vectors = np.where(self.alpha > 1e-3)[0]
self.support_vector_x = [X[i, :] for i in self.support_vectors]
self.support_vector_y = [y[i] for i in self.support_vectors]
self.support_vector_alpha = [self.alpha[i] for i in self.support_vectors]
# 顯示訓練過程
if show_train_process is True:
utils.plot_decision_function(X, y2, self, [i, best_j])
utils.plt.pause(0.1)
utils.plt.clf()
# 如果所有的點都滿足KKT條件,則中止
if if_all_match_kkt is True:
break
# 顯示最終結果
if show_train_process is True:
utils.plot_decision_function(X, y2, self, self.support_vectors)
utils.plt.show()
def get_params(self):
"""
輸出原始的係數
:return: w
"""
return self.w, self.b
def predict_proba(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
return utils.sigmoid(self.f(x))
def predict(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
proba = self.predict_proba(x)
return (proba >= 0.5).astype(int)
```
### 五.檢視效果
```python
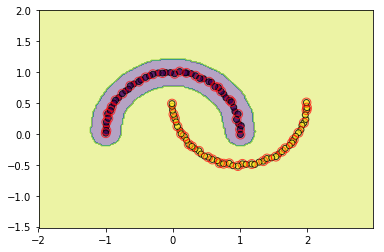
#檢視rbf的效果
svm = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```
```python
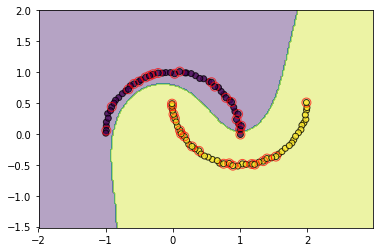
#檢視poly的效果
svm = SVC(C=3.0, kernel='poly',degree=3, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```
### 六.問題討論
#### 1.RBF函式中$\sigma$的不同取值對訓練的影響
為了探索該問題,我們對$\sigma$從小到大取一組數,在另外一個偽資料上檢視效果
```python
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
```
```python
c1 = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.01)
c1.fit(data, target)
c2 = SVC(C=3.0, kernel='rbf',gamma=0.5, epochs=10, tol=0.01)
c2.fit(data, target)
c3 = SVC(C=3.0, kernel='rbf',gamma=2, epochs=10, tol=0.01)
c3.fit(data, target)
```
```python
plt.figure(figsize=(16,4))
plt.subplot(1,3,1)
utils.plot_decision_function(data,target,c1)
plt.subplot(1,3,2)
utils.plot_decision_function(data,target,c2)
plt.subplot(1,3,3)
utils.plot_decision_function(data,target,c3)
```
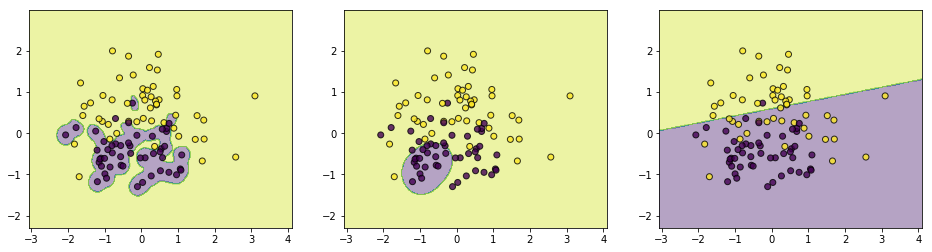
上面$\sigma$分別取值$[0.1,0.5,2]$,通過結果可以簡單總結如下:
(1)如果$\sigma$取值越小,SVM越能抓住個別樣本的資訊,越容易過擬合;
(2)$\sigma$取值越大SVM的泛化能力越強
如何對該結果進行理解呢?可以通過樣本點在對映空間的距離來看,對任意兩個樣本點$x,z$,它們在對映空間中的距離的平方可以表示如下:
$$
||\phi(x)-\phi(z)||^2=(\phi(x)-\phi(z))^T(\phi(x)-\phi(z))\\
=\phi(x)^T\phi(x)+\phi(z)^T\phi(z)-2\phi(x)^T\phi(z)\\
=K(x,x)+K(z,z)-2K(x,z)\\
=2-2\cdot exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})(將K(x,z)替換為RBF函式)
$$
所以:
(1)如果$\sigma\rightarrow 0$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow -\infty$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 0$,那麼$||\phi(x)-\phi(z)||\rightarrow \sqrt 2$
(2)如果$\sigma\rightarrow \infty$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow 0$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 1$,那麼$||\phi(x)-\phi(z)||\rightarrow 0$
我們可以驗證上面的總結,若$\sigma$取值越小,樣本點在對映空間越分散,則在高維空間越容易線性可分,表現在低維空間則越容易過擬合;$\sigma$取值越大,樣本點在對映空間越集中,越不易線性可分,表現在低維空間也是不易線性可分
#### 2.如何理解RBF可將資料對映到無限維空間
原諒自己,這部分公式不想碼了,具體內容參考大神的[知乎帖子>>>](https://zhuanlan.zhihu.com/p/58585604),其中主要需要用到兩個等式變換:
(1)指數函式的泰勒級數:$e^x=\sum_{n=1}^{\infty}\frac{x^n}{n!}$,將RBF函式進行展開;
(2)利用多項式展開定理,將樣本$x$與$z$在原始空間的內積的$n$次方進行展開,假如$x,z\in R^k$,那麼:
$$
(x^Tz)^n=(\sum_{i=1}^kx_iz_i)^n\\
=\sum_{l=1}^L\frac{n!}{n_{l_1}!n_{l_2}!\cdots n_{l_k}!}(x_1z_1)^{n_{l_1}}(x_2z_2)^{n_{l_2}}\cdots (x_kz_k)^{n_{l_k}}
$$
這裡,$\sum_{i=1}^kn_{l_i}=n$,$L=\frac{(n+k-1)!}{n!(k-1)!}$,進一步的,上面等式可以化簡為形如這樣的表示式:$\Phi(x)^T\Phi(z)$,$\Phi(x)=[\Phi_1(x),\Phi_2(x),\cdots ,\Phi
#### 利用核技巧後的SVM
所以,如果對原始資料施加一個對映,此時軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_i\phi(x_i)^T\phi(x)+b^*)
$$
### 三.核函式
觀察一下上面公式,我們的目的其實是求解$\phi(x_i)^T\phi(x_j)$,有沒有一種函式讓$(x_i,x_j)$只在原始空間做計算就達到$\phi(x_i)^T\phi(x_j)$的效果呢?有的,那就是核函式,即:
$$
K(x_i,x_j)=\phi(x_i)^T\phi(x_j)
$$
#### 怎樣的函式才能做核函式?
要成為核函式必須滿足如下兩點條件:
(1)對稱性:$K(x_i,x_j)=K(x_j,x_i)$
(2)正定性:對任意的$x_i,i=1,2,..,m$,$K(x,z)$對應的Gramm矩陣:
$$
K=[K(x_i,x_j)]_{m\times m}
$$
是半正定矩陣,這裡的$x_i\in$可行域,並不要求一定要屬於樣本集
#### 常見的核函式有哪些?
目前用的比較多的核函式有如下一些:
(1)多項式核函式:
$$
K(x,z)=(x^Tz+1)^p
$$
(2)高斯核函式:
$$
K(x,z)=exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})
$$
顯然,線性可分SVM中使用的是$K(x,z)=x^Tz$也是核函式
#### 利用核函式後的SVM
利用核函式後,軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_iK(x,x_i)+b^*)
$$
### 四.程式碼實現
程式碼實現很簡單,就在軟間隔SVM的基礎上將向量的內積計算$x^Tz$替換為$K(x,z)$即可,首先定義一些核函式:
```python
"""
該部分放到ml_model.kernel_functions中
"""
def linear():
"""
線性核函式
:return:linear function
"""
def _linear(x, y):
return np.dot(x, y)
return _linear
def poly(p=2):
"""
多項式核函式
:param p:
:return: poly function
"""
def _poly(x, y):
return np.power(np.dot(x, y) + 1, p)
return _poly
def rbf(sigma=0.1):
"""
徑向基/高斯核函式
:param sigma:
:return:
"""
def _rbf(x, y):
np_x = np.asarray(x)
if np_x.ndim <= 1:
return np.exp((-1 * np.dot(x - y, x - y) / (2 * sigma * sigma)))
else:
return np.exp((-1 * np.multiply(x - y, x - y).sum(axis=1) / (2 * sigma * sigma)))
return _rbf
```
```python
from ml_models import kernel_functions
class SVC(object):
def __init__(self, epochs=100, C=1.0, tol=1e-3, kernel=None, degree=3, gamma=0.1):
"""
:param epochs: 迭代次數上限
:param C: C越小,對於誤分類的懲罰越小
:param tol:提前中止訓練時的誤差值上限,避免迭代太久
:param kernel:核函式
:param degree:kernel='poly'時生效
:param gamma:kernel='rbf'時生效
"""
self.b = None
self.alpha = None
self.E = None
self.epochs = epochs
self.C = C
self.tol = tol
# 定義核函式
if kernel is None:
self.kernel_function = kernel_functions.linear()
elif kernel == 'poly':
self.kernel_function = kernel_functions.poly(degree)
elif kernel == 'rbf':
self.kernel_function = kernel_functions.rbf(gamma)
else:
self.kernel_function = kernel_functions.linear()
# 記錄支援向量
self.support_vectors = None
# 記錄支援向量的x
self.support_vector_x = []
# 記錄支援向量的y
self.support_vector_y = []
# 記錄支援向量的alpha
self.support_vector_alpha = []
def f(self, x):
"""
:param x:
:return: wx+b
"""
x_np = np.asarray(x)
if len(self.support_vector_x) == 0:
if x_np.ndim <= 1:
return 0
else:
return np.zeros((x_np.shape[:-1]))
else:
if x_np.ndim <= 1:
wx = 0
else:
wx = np.zeros((x_np.shape[:-1]))
for i in range(0, len(self.support_vector_x)):
wx += self.kernel_function(x, self.support_vector_x[i]) * self.support_vector_alpha[i] * \
self.support_vector_y[i]
return wx + self.b
def init_params(self, X, y):
"""
:param X: (n_samples,n_features)
:param y: (n_samples,) y_i\in\{0,1\}
:return:
"""
n_samples, n_features = X.shape
self.b = .0
self.alpha = np.zeros(n_samples)
self.E = np.zeros(n_samples)
# 初始化E
for i in range(0, n_samples):
self.E[i] = self.f(X[i, :]) - y[i]
def _select_j(self, best_i):
"""
選擇j
:param best_i:
:return:
"""
valid_j_list = [i for i in range(0, len(self.alpha)) if self.alpha[i] > 0 and i != best_i]
best_j = -1
# 優先選擇使得|E_i-E_j|最大的j
if len(valid_j_list) > 0:
max_e = 0
for j in valid_j_list:
current_e = np.abs(self.E[best_i] - self.E[j])
if current_e > max_e:
best_j = j
max_e = current_e
else:
# 隨機選擇
l = list(range(len(self.alpha)))
seq = l[: best_i] + l[best_i + 1:]
best_j = random.choice(seq)
return best_j
def _meet_kkt(self, x_i, y_i, alpha_i):
"""
判斷是否滿足KKT條件
:param w:
:param b:
:param x_i:
:param y_i:
:return:
"""
if alpha_i < self.C:
return y_i * self.f(x_i) >= 1 - self.tol
else:
return y_i * self.f(x_i) <= 1 + self.tol
def fit(self, X, y2, show_train_process=False):
"""
:param X:
:param y2:
:param show_train_process: 顯示訓練過程
:return:
"""
y = copy.deepcopy(y2)
y[y == 0] = -1
# 初始化引數
self.init_params(X, y)
for _ in range(0, self.epochs):
if_all_match_kkt = True
for i in range(0, len(self.alpha)):
x_i = X[i, :]
y_i = y[i]
alpha_i_old = self.alpha[i]
E_i_old = self.E[i]
# 外層迴圈:選擇違反KKT條件的點i
if not self._meet_kkt(x_i, y_i, alpha_i_old):
if_all_match_kkt = False
# 內層迴圈,選擇使|Ei-Ej|最大的點j
best_j = self._select_j(i)
alpha_j_old = self.alpha[best_j]
x_j = X[best_j, :]
y_j = y[best_j]
E_j_old = self.E[best_j]
# 進行更新
# 1.首先獲取無裁剪的最優alpha_2
eta = self.kernel_function(x_i, x_i) + self.kernel_function(x_j, x_j) - 2.0 * self.kernel_function(
x_i, x_j)
# 如果x_i和x_j很接近,則跳過
if eta < 1e-3:
continue
alpha_j_unc = alpha_j_old + y_j * (E_i_old - E_j_old) / eta
# 2.裁剪並得到new alpha_2
if y_i == y_j:
L = max(0., alpha_i_old + alpha_j_old - self.C)
H = min(self.C, alpha_i_old + alpha_j_old)
else:
L = max(0, alpha_j_old - alpha_i_old)
H = min(self.C, self.C + alpha_j_old - alpha_i_old)
if alpha_j_unc < L:
alpha_j_new = L
elif alpha_j_unc > H:
alpha_j_new = H
else:
alpha_j_new = alpha_j_unc
# 如果變化不夠大則跳過
if np.abs(alpha_j_new - alpha_j_old) < 1e-5:
continue
# 3.得到alpha_1_new
alpha_i_new = alpha_i_old + y_i * y_j * (alpha_j_old - alpha_j_new)
# 5.更新alpha_1,alpha_2
self.alpha[i] = alpha_i_new
self.alpha[best_j] = alpha_j_new
# 6.更新b
b_i_new = y_i - self.f(x_i) + self.b
b_j_new = y_j - self.f(x_j) + self.b
if self.C > alpha_i_new > 0:
self.b = b_i_new
elif self.C > alpha_j_new > 0:
self.b = b_j_new
else:
self.b = (b_i_new + b_j_new) / 2.0
# 7.更新E
for k in range(0, len(self.E)):
self.E[k] = self.f(X[k, :]) - y[k]
# 8.更新支援向量相關的資訊
self.support_vectors = np.where(self.alpha > 1e-3)[0]
self.support_vector_x = [X[i, :] for i in self.support_vectors]
self.support_vector_y = [y[i] for i in self.support_vectors]
self.support_vector_alpha = [self.alpha[i] for i in self.support_vectors]
# 顯示訓練過程
if show_train_process is True:
utils.plot_decision_function(X, y2, self, [i, best_j])
utils.plt.pause(0.1)
utils.plt.clf()
# 如果所有的點都滿足KKT條件,則中止
if if_all_match_kkt is True:
break
# 顯示最終結果
if show_train_process is True:
utils.plot_decision_function(X, y2, self, self.support_vectors)
utils.plt.show()
def get_params(self):
"""
輸出原始的係數
:return: w
"""
return self.w, self.b
def predict_proba(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
return utils.sigmoid(self.f(x))
def predict(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
proba = self.predict_proba(x)
return (proba >= 0.5).astype(int)
```
### 五.檢視效果
```python
#檢視rbf的效果
svm = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```

```python
#檢視poly的效果
svm = SVC(C=3.0, kernel='poly',degree=3, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```

### 六.問題討論
#### 1.RBF函式中$\sigma$的不同取值對訓練的影響
為了探索該問題,我們對$\sigma$從小到大取一組數,在另外一個偽資料上檢視效果
```python
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
```
```python
c1 = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.01)
c1.fit(data, target)
c2 = SVC(C=3.0, kernel='rbf',gamma=0.5, epochs=10, tol=0.01)
c2.fit(data, target)
c3 = SVC(C=3.0, kernel='rbf',gamma=2, epochs=10, tol=0.01)
c3.fit(data, target)
```
```python
plt.figure(figsize=(16,4))
plt.subplot(1,3,1)
utils.plot_decision_function(data,target,c1)
plt.subplot(1,3,2)
utils.plot_decision_function(data,target,c2)
plt.subplot(1,3,3)
utils.plot_decision_function(data,target,c3)
```

上面$\sigma$分別取值$[0.1,0.5,2]$,通過結果可以簡單總結如下:
(1)如果$\sigma$取值越小,SVM越能抓住個別樣本的資訊,越容易過擬合;
(2)$\sigma$取值越大SVM的泛化能力越強
如何對該結果進行理解呢?可以通過樣本點在對映空間的距離來看,對任意兩個樣本點$x,z$,它們在對映空間中的距離的平方可以表示如下:
$$
||\phi(x)-\phi(z)||^2=(\phi(x)-\phi(z))^T(\phi(x)-\phi(z))\\
=\phi(x)^T\phi(x)+\phi(z)^T\phi(z)-2\phi(x)^T\phi(z)\\
=K(x,x)+K(z,z)-2K(x,z)\\
=2-2\cdot exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})(將K(x,z)替換為RBF函式)
$$
所以:
(1)如果$\sigma\rightarrow 0$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow -\infty$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 0$,那麼$||\phi(x)-\phi(z)||\rightarrow \sqrt 2$
(2)如果$\sigma\rightarrow \infty$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow 0$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 1$,那麼$||\phi(x)-\phi(z)||\rightarrow 0$
我們可以驗證上面的總結,若$\sigma$取值越小,樣本點在對映空間越分散,則在高維空間越容易線性可分,表現在低維空間則越容易過擬合;$\sigma$取值越大,樣本點在對映空間越集中,越不易線性可分,表現在低維空間也是不易線性可分
#### 2.如何理解RBF可將資料對映到無限維空間
原諒自己,這部分公式不想碼了,具體內容參考大神的[知乎帖子>>>](https://zhuanlan.zhihu.com/p/58585604),其中主要需要用到兩個等式變換:
(1)指數函式的泰勒級數:$e^x=\sum_{n=1}^{\infty}\frac{x^n}{n!}$,將RBF函式進行展開;
(2)利用多項式展開定理,將樣本$x$與$z$在原始空間的內積的$n$次方進行展開,假如$x,z\in R^k$,那麼:
$$
(x^Tz)^n=(\sum_{i=1}^kx_iz_i)^n\\
=\sum_{l=1}^L\frac{n!}{n_{l_1}!n_{l_2}!\cdots n_{l_k}!}(x_1z_1)^{n_{l_1}}(x_2z_2)^{n_{l_2}}\cdots (x_kz_k)^{n_{l_k}}
$$
這裡,$\sum_{i=1}^kn_{l_i}=n$,$L=\frac{(n+k-1)!}{n!(k-1)!}$,進一步的,上面等式可以化簡為形如這樣的表示式:$\Phi(x)^T\Phi(z)$,$\Phi(x)=[\Phi_1(x),\Phi_2(x),\cdots ,\Phi
 #### 利用核技巧後的SVM
所以,如果對原始資料施加一個對映,此時軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_i\phi(x_i)^T\phi(x)+b^*)
$$
### 三.核函式
觀察一下上面公式,我們的目的其實是求解$\phi(x_i)^T\phi(x_j)$,有沒有一種函式讓$(x_i,x_j)$只在原始空間做計算就達到$\phi(x_i)^T\phi(x_j)$的效果呢?有的,那就是核函式,即:
$$
K(x_i,x_j)=\phi(x_i)^T\phi(x_j)
$$
#### 怎樣的函式才能做核函式?
要成為核函式必須滿足如下兩點條件:
(1)對稱性:$K(x_i,x_j)=K(x_j,x_i)$
(2)正定性:對任意的$x_i,i=1,2,..,m$,$K(x,z)$對應的Gramm矩陣:
$$
K=[K(x_i,x_j)]_{m\times m}
$$
是半正定矩陣,這裡的$x_i\in$可行域,並不要求一定要屬於樣本集
#### 常見的核函式有哪些?
目前用的比較多的核函式有如下一些:
(1)多項式核函式:
$$
K(x,z)=(x^Tz+1)^p
$$
(2)高斯核函式:
$$
K(x,z)=exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})
$$
顯然,線性可分SVM中使用的是$K(x,z)=x^Tz$也是核函式
#### 利用核函式後的SVM
利用核函式後,軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_iK(x,x_i)+b^*)
$$
### 四.程式碼實現
程式碼實現很簡單,就在軟間隔SVM的基礎上將向量的內積計算$x^Tz$替換為$K(x,z)$即可,首先定義一些核函式:
```python
"""
該部分放到ml_model.kernel_functions中
"""
def linear():
"""
線性核函式
:return:linear function
"""
def _linear(x, y):
return np.dot(x, y)
return _linear
def poly(p=2):
"""
多項式核函式
:param p:
:return: poly function
"""
def _poly(x, y):
return np.power(np.dot(x, y) + 1, p)
return _poly
def rbf(sigma=0.1):
"""
徑向基/高斯核函式
:param sigma:
:return:
"""
def _rbf(x, y):
np_x = np.asarray(x)
if np_x.ndim <= 1:
return np.exp((-1 * np.dot(x - y, x - y) / (2 * sigma * sigma)))
else:
return np.exp((-1 * np.multiply(x - y, x - y).sum(axis=1) / (2 * sigma * sigma)))
return _rbf
```
```python
from ml_models import kernel_functions
class SVC(object):
def __init__(self, epochs=100, C=1.0, tol=1e-3, kernel=None, degree=3, gamma=0.1):
"""
:param epochs: 迭代次數上限
:param C: C越小,對於誤分類的懲罰越小
:param tol:提前中止訓練時的誤差值上限,避免迭代太久
:param kernel:核函式
:param degree:kernel='poly'時生效
:param gamma:kernel='rbf'時生效
"""
self.b = None
self.alpha = None
self.E = None
self.epochs = epochs
self.C = C
self.tol = tol
# 定義核函式
if kernel is None:
self.kernel_function = kernel_functions.linear()
elif kernel == 'poly':
self.kernel_function = kernel_functions.poly(degree)
elif kernel == 'rbf':
self.kernel_function = kernel_functions.rbf(gamma)
else:
self.kernel_function = kernel_functions.linear()
# 記錄支援向量
self.support_vectors = None
# 記錄支援向量的x
self.support_vector_x = []
# 記錄支援向量的y
self.support_vector_y = []
# 記錄支援向量的alpha
self.support_vector_alpha = []
def f(self, x):
"""
:param x:
:return: wx+b
"""
x_np = np.asarray(x)
if len(self.support_vector_x) == 0:
if x_np.ndim <= 1:
return 0
else:
return np.zeros((x_np.shape[:-1]))
else:
if x_np.ndim <= 1:
wx = 0
else:
wx = np.zeros((x_np.shape[:-1]))
for i in range(0, len(self.support_vector_x)):
wx += self.kernel_function(x, self.support_vector_x[i]) * self.support_vector_alpha[i] * \
self.support_vector_y[i]
return wx + self.b
def init_params(self, X, y):
"""
:param X: (n_samples,n_features)
:param y: (n_samples,) y_i\in\{0,1\}
:return:
"""
n_samples, n_features = X.shape
self.b = .0
self.alpha = np.zeros(n_samples)
self.E = np.zeros(n_samples)
# 初始化E
for i in range(0, n_samples):
self.E[i] = self.f(X[i, :]) - y[i]
def _select_j(self, best_i):
"""
選擇j
:param best_i:
:return:
"""
valid_j_list = [i for i in range(0, len(self.alpha)) if self.alpha[i] > 0 and i != best_i]
best_j = -1
# 優先選擇使得|E_i-E_j|最大的j
if len(valid_j_list) > 0:
max_e = 0
for j in valid_j_list:
current_e = np.abs(self.E[best_i] - self.E[j])
if current_e > max_e:
best_j = j
max_e = current_e
else:
# 隨機選擇
l = list(range(len(self.alpha)))
seq = l[: best_i] + l[best_i + 1:]
best_j = random.choice(seq)
return best_j
def _meet_kkt(self, x_i, y_i, alpha_i):
"""
判斷是否滿足KKT條件
:param w:
:param b:
:param x_i:
:param y_i:
:return:
"""
if alpha_i < self.C:
return y_i * self.f(x_i) >= 1 - self.tol
else:
return y_i * self.f(x_i) <= 1 + self.tol
def fit(self, X, y2, show_train_process=False):
"""
:param X:
:param y2:
:param show_train_process: 顯示訓練過程
:return:
"""
y = copy.deepcopy(y2)
y[y == 0] = -1
# 初始化引數
self.init_params(X, y)
for _ in range(0, self.epochs):
if_all_match_kkt = True
for i in range(0, len(self.alpha)):
x_i = X[i, :]
y_i = y[i]
alpha_i_old = self.alpha[i]
E_i_old = self.E[i]
# 外層迴圈:選擇違反KKT條件的點i
if not self._meet_kkt(x_i, y_i, alpha_i_old):
if_all_match_kkt = False
# 內層迴圈,選擇使|Ei-Ej|最大的點j
best_j = self._select_j(i)
alpha_j_old = self.alpha[best_j]
x_j = X[best_j, :]
y_j = y[best_j]
E_j_old = self.E[best_j]
# 進行更新
# 1.首先獲取無裁剪的最優alpha_2
eta = self.kernel_function(x_i, x_i) + self.kernel_function(x_j, x_j) - 2.0 * self.kernel_function(
x_i, x_j)
# 如果x_i和x_j很接近,則跳過
if eta < 1e-3:
continue
alpha_j_unc = alpha_j_old + y_j * (E_i_old - E_j_old) / eta
# 2.裁剪並得到new alpha_2
if y_i == y_j:
L = max(0., alpha_i_old + alpha_j_old - self.C)
H = min(self.C, alpha_i_old + alpha_j_old)
else:
L = max(0, alpha_j_old - alpha_i_old)
H = min(self.C, self.C + alpha_j_old - alpha_i_old)
if alpha_j_unc < L:
alpha_j_new = L
elif alpha_j_unc > H:
alpha_j_new = H
else:
alpha_j_new = alpha_j_unc
# 如果變化不夠大則跳過
if np.abs(alpha_j_new - alpha_j_old) < 1e-5:
continue
# 3.得到alpha_1_new
alpha_i_new = alpha_i_old + y_i * y_j * (alpha_j_old - alpha_j_new)
# 5.更新alpha_1,alpha_2
self.alpha[i] = alpha_i_new
self.alpha[best_j] = alpha_j_new
# 6.更新b
b_i_new = y_i - self.f(x_i) + self.b
b_j_new = y_j - self.f(x_j) + self.b
if self.C > alpha_i_new > 0:
self.b = b_i_new
elif self.C > alpha_j_new > 0:
self.b = b_j_new
else:
self.b = (b_i_new + b_j_new) / 2.0
# 7.更新E
for k in range(0, len(self.E)):
self.E[k] = self.f(X[k, :]) - y[k]
# 8.更新支援向量相關的資訊
self.support_vectors = np.where(self.alpha > 1e-3)[0]
self.support_vector_x = [X[i, :] for i in self.support_vectors]
self.support_vector_y = [y[i] for i in self.support_vectors]
self.support_vector_alpha = [self.alpha[i] for i in self.support_vectors]
# 顯示訓練過程
if show_train_process is True:
utils.plot_decision_function(X, y2, self, [i, best_j])
utils.plt.pause(0.1)
utils.plt.clf()
# 如果所有的點都滿足KKT條件,則中止
if if_all_match_kkt is True:
break
# 顯示最終結果
if show_train_process is True:
utils.plot_decision_function(X, y2, self, self.support_vectors)
utils.plt.show()
def get_params(self):
"""
輸出原始的係數
:return: w
"""
return self.w, self.b
def predict_proba(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
return utils.sigmoid(self.f(x))
def predict(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
proba = self.predict_proba(x)
return (proba >= 0.5).astype(int)
```
### 五.檢視效果
```python
#檢視rbf的效果
svm = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```

```python
#檢視poly的效果
svm = SVC(C=3.0, kernel='poly',degree=3, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```

### 六.問題討論
#### 1.RBF函式中$\sigma$的不同取值對訓練的影響
為了探索該問題,我們對$\sigma$從小到大取一組數,在另外一個偽資料上檢視效果
```python
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
```
```python
c1 = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.01)
c1.fit(data, target)
c2 = SVC(C=3.0, kernel='rbf',gamma=0.5, epochs=10, tol=0.01)
c2.fit(data, target)
c3 = SVC(C=3.0, kernel='rbf',gamma=2, epochs=10, tol=0.01)
c3.fit(data, target)
```
```python
plt.figure(figsize=(16,4))
plt.subplot(1,3,1)
utils.plot_decision_function(data,target,c1)
plt.subplot(1,3,2)
utils.plot_decision_function(data,target,c2)
plt.subplot(1,3,3)
utils.plot_decision_function(data,target,c3)
```

上面$\sigma$分別取值$[0.1,0.5,2]$,通過結果可以簡單總結如下:
(1)如果$\sigma$取值越小,SVM越能抓住個別樣本的資訊,越容易過擬合;
(2)$\sigma$取值越大SVM的泛化能力越強
如何對該結果進行理解呢?可以通過樣本點在對映空間的距離來看,對任意兩個樣本點$x,z$,它們在對映空間中的距離的平方可以表示如下:
$$
||\phi(x)-\phi(z)||^2=(\phi(x)-\phi(z))^T(\phi(x)-\phi(z))\\
=\phi(x)^T\phi(x)+\phi(z)^T\phi(z)-2\phi(x)^T\phi(z)\\
=K(x,x)+K(z,z)-2K(x,z)\\
=2-2\cdot exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})(將K(x,z)替換為RBF函式)
$$
所以:
(1)如果$\sigma\rightarrow 0$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow -\infty$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 0$,那麼$||\phi(x)-\phi(z)||\rightarrow \sqrt 2$
(2)如果$\sigma\rightarrow \infty$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow 0$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 1$,那麼$||\phi(x)-\phi(z)||\rightarrow 0$
我們可以驗證上面的總結,若$\sigma$取值越小,樣本點在對映空間越分散,則在高維空間越容易線性可分,表現在低維空間則越容易過擬合;$\sigma$取值越大,樣本點在對映空間越集中,越不易線性可分,表現在低維空間也是不易線性可分
#### 2.如何理解RBF可將資料對映到無限維空間
原諒自己,這部分公式不想碼了,具體內容參考大神的[知乎帖子>>>](https://zhuanlan.zhihu.com/p/58585604),其中主要需要用到兩個等式變換:
(1)指數函式的泰勒級數:$e^x=\sum_{n=1}^{\infty}\frac{x^n}{n!}$,將RBF函式進行展開;
(2)利用多項式展開定理,將樣本$x$與$z$在原始空間的內積的$n$次方進行展開,假如$x,z\in R^k$,那麼:
$$
(x^Tz)^n=(\sum_{i=1}^kx_iz_i)^n\\
=\sum_{l=1}^L\frac{n!}{n_{l_1}!n_{l_2}!\cdots n_{l_k}!}(x_1z_1)^{n_{l_1}}(x_2z_2)^{n_{l_2}}\cdots (x_kz_k)^{n_{l_k}}
$$
這裡,$\sum_{i=1}^kn_{l_i}=n$,$L=\frac{(n+k-1)!}{n!(k-1)!}$,進一步的,上面等式可以化簡為形如這樣的表示式:$\Phi(x)^T\Phi(z)$,$\Phi(x)=[\Phi_1(x),\Phi_2(x),\cdots ,\Phi
#### 利用核技巧後的SVM
所以,如果對原始資料施加一個對映,此時軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_i\phi(x_i)^T\phi(x)+b^*)
$$
### 三.核函式
觀察一下上面公式,我們的目的其實是求解$\phi(x_i)^T\phi(x_j)$,有沒有一種函式讓$(x_i,x_j)$只在原始空間做計算就達到$\phi(x_i)^T\phi(x_j)$的效果呢?有的,那就是核函式,即:
$$
K(x_i,x_j)=\phi(x_i)^T\phi(x_j)
$$
#### 怎樣的函式才能做核函式?
要成為核函式必須滿足如下兩點條件:
(1)對稱性:$K(x_i,x_j)=K(x_j,x_i)$
(2)正定性:對任意的$x_i,i=1,2,..,m$,$K(x,z)$對應的Gramm矩陣:
$$
K=[K(x_i,x_j)]_{m\times m}
$$
是半正定矩陣,這裡的$x_i\in$可行域,並不要求一定要屬於樣本集
#### 常見的核函式有哪些?
目前用的比較多的核函式有如下一些:
(1)多項式核函式:
$$
K(x,z)=(x^Tz+1)^p
$$
(2)高斯核函式:
$$
K(x,z)=exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})
$$
顯然,線性可分SVM中使用的是$K(x,z)=x^Tz$也是核函式
#### 利用核函式後的SVM
利用核函式後,軟間隔SVM的對偶問題為:
$$
\min_{\alpha} \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum_{i=1}^N\alpha_i\\
s.t.\sum_{i=1}^N\alpha_iy_i=0,\\
0\leq\alpha_i\leq C,i=1,2,...,N
$$
求解得最優$\alpha_i^*$後,SVM模型為:
$$
f(x)=sign(\sum_{i=1}^N\alpha_iy_iK(x,x_i)+b^*)
$$
### 四.程式碼實現
程式碼實現很簡單,就在軟間隔SVM的基礎上將向量的內積計算$x^Tz$替換為$K(x,z)$即可,首先定義一些核函式:
```python
"""
該部分放到ml_model.kernel_functions中
"""
def linear():
"""
線性核函式
:return:linear function
"""
def _linear(x, y):
return np.dot(x, y)
return _linear
def poly(p=2):
"""
多項式核函式
:param p:
:return: poly function
"""
def _poly(x, y):
return np.power(np.dot(x, y) + 1, p)
return _poly
def rbf(sigma=0.1):
"""
徑向基/高斯核函式
:param sigma:
:return:
"""
def _rbf(x, y):
np_x = np.asarray(x)
if np_x.ndim <= 1:
return np.exp((-1 * np.dot(x - y, x - y) / (2 * sigma * sigma)))
else:
return np.exp((-1 * np.multiply(x - y, x - y).sum(axis=1) / (2 * sigma * sigma)))
return _rbf
```
```python
from ml_models import kernel_functions
class SVC(object):
def __init__(self, epochs=100, C=1.0, tol=1e-3, kernel=None, degree=3, gamma=0.1):
"""
:param epochs: 迭代次數上限
:param C: C越小,對於誤分類的懲罰越小
:param tol:提前中止訓練時的誤差值上限,避免迭代太久
:param kernel:核函式
:param degree:kernel='poly'時生效
:param gamma:kernel='rbf'時生效
"""
self.b = None
self.alpha = None
self.E = None
self.epochs = epochs
self.C = C
self.tol = tol
# 定義核函式
if kernel is None:
self.kernel_function = kernel_functions.linear()
elif kernel == 'poly':
self.kernel_function = kernel_functions.poly(degree)
elif kernel == 'rbf':
self.kernel_function = kernel_functions.rbf(gamma)
else:
self.kernel_function = kernel_functions.linear()
# 記錄支援向量
self.support_vectors = None
# 記錄支援向量的x
self.support_vector_x = []
# 記錄支援向量的y
self.support_vector_y = []
# 記錄支援向量的alpha
self.support_vector_alpha = []
def f(self, x):
"""
:param x:
:return: wx+b
"""
x_np = np.asarray(x)
if len(self.support_vector_x) == 0:
if x_np.ndim <= 1:
return 0
else:
return np.zeros((x_np.shape[:-1]))
else:
if x_np.ndim <= 1:
wx = 0
else:
wx = np.zeros((x_np.shape[:-1]))
for i in range(0, len(self.support_vector_x)):
wx += self.kernel_function(x, self.support_vector_x[i]) * self.support_vector_alpha[i] * \
self.support_vector_y[i]
return wx + self.b
def init_params(self, X, y):
"""
:param X: (n_samples,n_features)
:param y: (n_samples,) y_i\in\{0,1\}
:return:
"""
n_samples, n_features = X.shape
self.b = .0
self.alpha = np.zeros(n_samples)
self.E = np.zeros(n_samples)
# 初始化E
for i in range(0, n_samples):
self.E[i] = self.f(X[i, :]) - y[i]
def _select_j(self, best_i):
"""
選擇j
:param best_i:
:return:
"""
valid_j_list = [i for i in range(0, len(self.alpha)) if self.alpha[i] > 0 and i != best_i]
best_j = -1
# 優先選擇使得|E_i-E_j|最大的j
if len(valid_j_list) > 0:
max_e = 0
for j in valid_j_list:
current_e = np.abs(self.E[best_i] - self.E[j])
if current_e > max_e:
best_j = j
max_e = current_e
else:
# 隨機選擇
l = list(range(len(self.alpha)))
seq = l[: best_i] + l[best_i + 1:]
best_j = random.choice(seq)
return best_j
def _meet_kkt(self, x_i, y_i, alpha_i):
"""
判斷是否滿足KKT條件
:param w:
:param b:
:param x_i:
:param y_i:
:return:
"""
if alpha_i < self.C:
return y_i * self.f(x_i) >= 1 - self.tol
else:
return y_i * self.f(x_i) <= 1 + self.tol
def fit(self, X, y2, show_train_process=False):
"""
:param X:
:param y2:
:param show_train_process: 顯示訓練過程
:return:
"""
y = copy.deepcopy(y2)
y[y == 0] = -1
# 初始化引數
self.init_params(X, y)
for _ in range(0, self.epochs):
if_all_match_kkt = True
for i in range(0, len(self.alpha)):
x_i = X[i, :]
y_i = y[i]
alpha_i_old = self.alpha[i]
E_i_old = self.E[i]
# 外層迴圈:選擇違反KKT條件的點i
if not self._meet_kkt(x_i, y_i, alpha_i_old):
if_all_match_kkt = False
# 內層迴圈,選擇使|Ei-Ej|最大的點j
best_j = self._select_j(i)
alpha_j_old = self.alpha[best_j]
x_j = X[best_j, :]
y_j = y[best_j]
E_j_old = self.E[best_j]
# 進行更新
# 1.首先獲取無裁剪的最優alpha_2
eta = self.kernel_function(x_i, x_i) + self.kernel_function(x_j, x_j) - 2.0 * self.kernel_function(
x_i, x_j)
# 如果x_i和x_j很接近,則跳過
if eta < 1e-3:
continue
alpha_j_unc = alpha_j_old + y_j * (E_i_old - E_j_old) / eta
# 2.裁剪並得到new alpha_2
if y_i == y_j:
L = max(0., alpha_i_old + alpha_j_old - self.C)
H = min(self.C, alpha_i_old + alpha_j_old)
else:
L = max(0, alpha_j_old - alpha_i_old)
H = min(self.C, self.C + alpha_j_old - alpha_i_old)
if alpha_j_unc < L:
alpha_j_new = L
elif alpha_j_unc > H:
alpha_j_new = H
else:
alpha_j_new = alpha_j_unc
# 如果變化不夠大則跳過
if np.abs(alpha_j_new - alpha_j_old) < 1e-5:
continue
# 3.得到alpha_1_new
alpha_i_new = alpha_i_old + y_i * y_j * (alpha_j_old - alpha_j_new)
# 5.更新alpha_1,alpha_2
self.alpha[i] = alpha_i_new
self.alpha[best_j] = alpha_j_new
# 6.更新b
b_i_new = y_i - self.f(x_i) + self.b
b_j_new = y_j - self.f(x_j) + self.b
if self.C > alpha_i_new > 0:
self.b = b_i_new
elif self.C > alpha_j_new > 0:
self.b = b_j_new
else:
self.b = (b_i_new + b_j_new) / 2.0
# 7.更新E
for k in range(0, len(self.E)):
self.E[k] = self.f(X[k, :]) - y[k]
# 8.更新支援向量相關的資訊
self.support_vectors = np.where(self.alpha > 1e-3)[0]
self.support_vector_x = [X[i, :] for i in self.support_vectors]
self.support_vector_y = [y[i] for i in self.support_vectors]
self.support_vector_alpha = [self.alpha[i] for i in self.support_vectors]
# 顯示訓練過程
if show_train_process is True:
utils.plot_decision_function(X, y2, self, [i, best_j])
utils.plt.pause(0.1)
utils.plt.clf()
# 如果所有的點都滿足KKT條件,則中止
if if_all_match_kkt is True:
break
# 顯示最終結果
if show_train_process is True:
utils.plot_decision_function(X, y2, self, self.support_vectors)
utils.plt.show()
def get_params(self):
"""
輸出原始的係數
:return: w
"""
return self.w, self.b
def predict_proba(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
return utils.sigmoid(self.f(x))
def predict(self, x):
"""
:param x:ndarray格式資料: m x n
:return: m x 1
"""
proba = self.predict_proba(x)
return (proba >= 0.5).astype(int)
```
### 五.檢視效果
```python
#檢視rbf的效果
svm = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```

```python
#檢視poly的效果
svm = SVC(C=3.0, kernel='poly',degree=3, epochs=10, tol=0.2)
svm.fit(data, target)
utils.plot_decision_function(data, target, svm, svm.support_vectors)
```

### 六.問題討論
#### 1.RBF函式中$\sigma$的不同取值對訓練的影響
為了探索該問題,我們對$\sigma$從小到大取一組數,在另外一個偽資料上檢視效果
```python
from sklearn.datasets import make_classification
data, target = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=1, n_redundant=0,
n_repeated=0, n_clusters_per_class=1, class_sep=.5,random_state=21)
```
```python
c1 = SVC(C=3.0, kernel='rbf',gamma=0.1, epochs=10, tol=0.01)
c1.fit(data, target)
c2 = SVC(C=3.0, kernel='rbf',gamma=0.5, epochs=10, tol=0.01)
c2.fit(data, target)
c3 = SVC(C=3.0, kernel='rbf',gamma=2, epochs=10, tol=0.01)
c3.fit(data, target)
```
```python
plt.figure(figsize=(16,4))
plt.subplot(1,3,1)
utils.plot_decision_function(data,target,c1)
plt.subplot(1,3,2)
utils.plot_decision_function(data,target,c2)
plt.subplot(1,3,3)
utils.plot_decision_function(data,target,c3)
```

上面$\sigma$分別取值$[0.1,0.5,2]$,通過結果可以簡單總結如下:
(1)如果$\sigma$取值越小,SVM越能抓住個別樣本的資訊,越容易過擬合;
(2)$\sigma$取值越大SVM的泛化能力越強
如何對該結果進行理解呢?可以通過樣本點在對映空間的距離來看,對任意兩個樣本點$x,z$,它們在對映空間中的距離的平方可以表示如下:
$$
||\phi(x)-\phi(z)||^2=(\phi(x)-\phi(z))^T(\phi(x)-\phi(z))\\
=\phi(x)^T\phi(x)+\phi(z)^T\phi(z)-2\phi(x)^T\phi(z)\\
=K(x,x)+K(z,z)-2K(x,z)\\
=2-2\cdot exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})(將K(x,z)替換為RBF函式)
$$
所以:
(1)如果$\sigma\rightarrow 0$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow -\infty$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 0$,那麼$||\phi(x)-\phi(z)||\rightarrow \sqrt 2$
(2)如果$\sigma\rightarrow \infty$,那麼$-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2}\rightarrow 0$,那麼$exp(-\frac{\mid\mid x-z\mid\mid^2}{2\sigma^2})\rightarrow 1$,那麼$||\phi(x)-\phi(z)||\rightarrow 0$
我們可以驗證上面的總結,若$\sigma$取值越小,樣本點在對映空間越分散,則在高維空間越容易線性可分,表現在低維空間則越容易過擬合;$\sigma$取值越大,樣本點在對映空間越集中,越不易線性可分,表現在低維空間也是不易線性可分
#### 2.如何理解RBF可將資料對映到無限維空間
原諒自己,這部分公式不想碼了,具體內容參考大神的[知乎帖子>>>](https://zhuanlan.zhihu.com/p/58585604),其中主要需要用到兩個等式變換:
(1)指數函式的泰勒級數:$e^x=\sum_{n=1}^{\infty}\frac{x^n}{n!}$,將RBF函式進行展開;
(2)利用多項式展開定理,將樣本$x$與$z$在原始空間的內積的$n$次方進行展開,假如$x,z\in R^k$,那麼:
$$
(x^Tz)^n=(\sum_{i=1}^kx_iz_i)^n\\
=\sum_{l=1}^L\frac{n!}{n_{l_1}!n_{l_2}!\cdots n_{l_k}!}(x_1z_1)^{n_{l_1}}(x_2z_2)^{n_{l_2}}\cdots (x_kz_k)^{n_{l_k}}
$$
這裡,$\sum_{i=1}^kn_{l_i}=n$,$L=\frac{(n+k-1)!}{n!(k-1)!}$,進一步的,上面等式可以化簡為形如這樣的表示式:$\Phi(x)^T\Phi(z)$,$\Phi(x)=[\Phi_1(x),\Phi_2(x),\cdots ,\Phi
