失蹤人口迴歸，近期換工作一波三折，耽誤了不少時間，從今開始每週更新~

索引是一種支援快速查詢的資料結構，同時索引優化也是後端工程師的必會知識點。各個公司都有所謂的MySQL”軍規“，其實這些所謂的優化和規定，並不是什麼高深的技術，只是要求大家正確建立和使用索引而已。工欲善其事必先利其器，想要正確運用索引，需要了解其底層實現原理，本文將探索關於索引的“是什麼”以及”為什麼“。

MySQL中關於索引的概念有很多，為了避免混淆，在上一篇文章中關於索引在不同維度分類設計到的一些名詞進行了解釋，如輔助索引，唯一索引，覆蓋索引，B+Tree索引…., 牆裂建議不明白的小夥伴可以先去看看圖解MySQL索引(上)—聊聊索引的分類，本文中關於索引型別的各種定義不再複述。

一，磁碟IO問題

1.1 磁碟IO

所謂磁碟IO，簡單來講就是就是將磁碟中的資料讀取到記憶體或者是從記憶體寫入磁碟。在系統開發與設計過程中，磁碟IO的瓶頸往往不可忽略，因為這是一個相對比較耗時的操作。

上圖是一個機械硬碟，雖然速度不如SSD，但是由於價格低廉，目前仍是主流的儲存介質。它的IO操作通常需要尋道，旋轉和傳輸三個步驟。

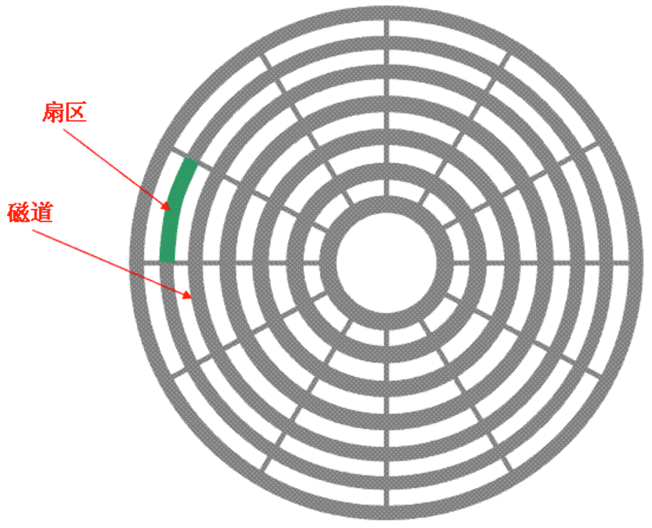
尋道，是指將讀寫磁頭移動到正確的磁軌，尋道時間越短，IO操作越快，目前磁碟的平均尋道時間一般在3-15ms左右。

旋轉，是指將碟片旋轉到請求資料所在的扇區，這部分所需要的時間由硬碟的配置所決定。旋轉延遲由磁碟轉速所決定，也就是常說的7200轉和5400轉等。

例如，7200轉是指每分鐘可以旋轉7200圈，那麼旋轉一圈所需要的時間就是60*1000/7200 ≈ 8.33ms，而旋轉延遲通常取旋轉一週時間的1/2，也就是大約4.17ms。

傳輸，磁碟傳輸的速度通常在幾十到上百M每秒，假設速度為20M/s，要傳輸的資料為64kb，則傳輸時間則是 64 / 1024 / 20 * 1000 = 3.125ms。不過目前流行的SSD傳輸速度大幅度提升，SATA Ⅱ可以達到300M/s，傳輸速度往往遠小於前兩步操作所以傳輸時間往往可以忽略不記。

機械硬碟的連續讀寫效能很好，但隨機讀寫效能很差，這主要是因為磁頭移動到正確的磁軌上需要時間，隨機讀寫時，磁頭需要不停的移動，時間都浪費在了磁頭定址上，所以效能不高。

上述過程是對傳統機械磁碟IO延遲的粗略介紹，目的是告訴大家磁碟IO過程是個耗時的過程，記憶體操作往往與之速度不在同一個數量級。即使是目前比較流行的SSD，想必記憶體中資料讀取效能也差之千里。

1.2 區域性性原理

由於磁碟IO是一個比較耗時的操作，而作業系統在設計時則定義一個空間區域性性原則，區域性性原理是指CPU訪問儲存器時，無論是存取指令還是存取資料，所訪問的儲存單元都趨於聚集在一個較小的連續區域中。

在作業系統的檔案系統中，資料也是按照page劃分的，一般為4k或8k。當計算機訪問一個地址資料時，不僅會載入當前資料所在的資料頁，還會將當前資料頁相鄰的資料頁一同載入到記憶體。而這個過程實際上只發生了1次磁碟IO，這個理論對於索引的資料結構設計非常有幫助。

二，索引資料結構演進

索引是一種支援快速查詢的資料結構，在運用中往往還要求能夠支援順序查詢，而常見的資料結構有很多，比如陣列，連結串列，二叉樹，散列表，二叉搜尋樹，平衡搜尋二叉樹，紅黑樹，跳錶等。僅僅從資料結構那麼為什麼選擇B+Tree呢？

首先對於陣列，連結串列這種線性表來說，適合儲存資料，而不是查詢資料，同樣，對於普通二叉樹來說，資料儲存沒有特定規律，所以也不適合。

2.1 雜湊索引不能滿足業務需求

雜湊（Hash）是一種非常快的查詢方法，在一般情況下這種查詢的時間複雜度為O（1），即一般僅需要一次查詢就能定位到資料。在各種程式語言和資料庫中應用廣泛，如Java，Python，Redis中都有使用。

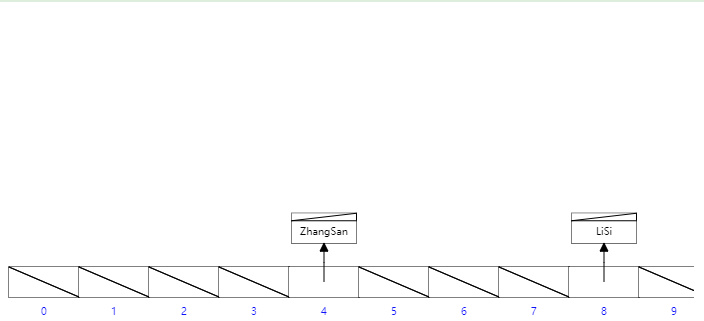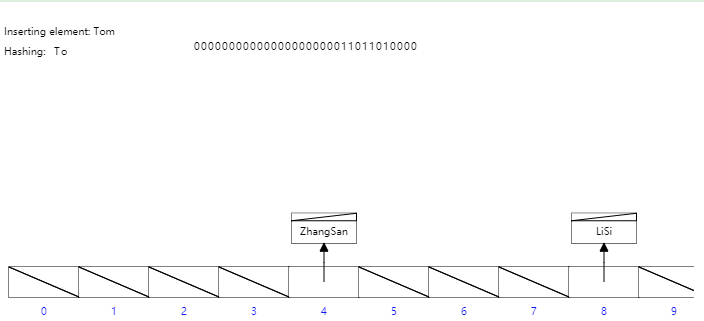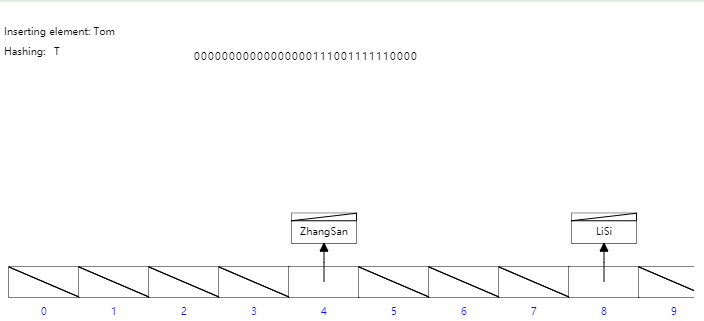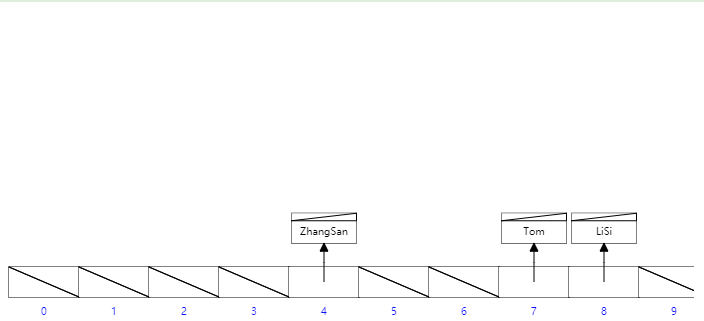
雜湊結構在單條資料的等值查詢是效能非常優秀，但是隻能用來搜尋等值的查詢， 對於範圍查詢，模糊查詢（最左字首原則）都不支援，所以不能很好的支援業務需求；所以MySQL並沒有顯式支援Hash索引，而是根據資料的訪問頻次和模式自動的為熱點資料頁建立雜湊索引，稱之為自適應雜湊索引。

並且由於雜湊函式的隨機性，Hash索引通常都是隨機的記憶體訪問，對於快取不友好，會造成頻繁的磁碟IO。

2.2 二叉搜尋樹退化成連結串列

二叉搜尋樹，如果左子樹不為空，則左子樹上所有節點均小於根節點，右子樹節點均大於根節點；由其屬性不難看出，這種樹非常適合資料查詢。不過有個致命的缺點是二叉搜尋樹的樹型取決於資料的輸入順序，極端情況下會退化成連結串列。

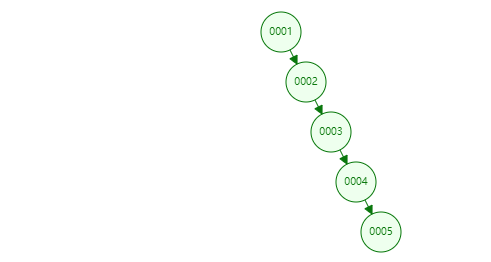
2.3 平衡二叉搜尋樹過於嚴格

為了解決上述問題，平衡二叉搜尋樹就誕生了。在保證資料順序的基礎上，又能維持樹型，保證每個節點的左右子樹高度相差不超過1。

不過由於要維持樹的平衡，在插入資料時可能要進行大量的資料移動。平衡搜尋二叉樹過於嚴格的平衡要求，導致幾乎每次插入和刪除節點都會破壞樹的平衡性，使得樹的效能大打折扣。

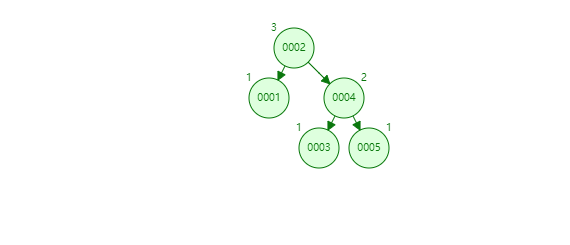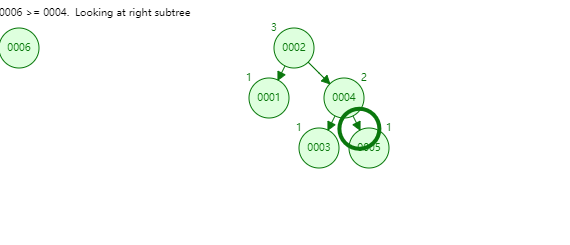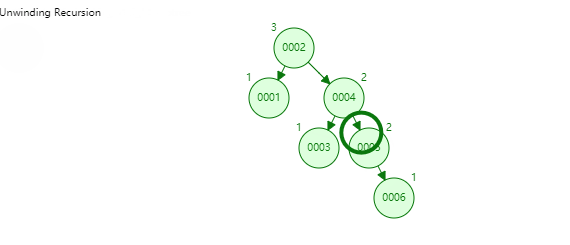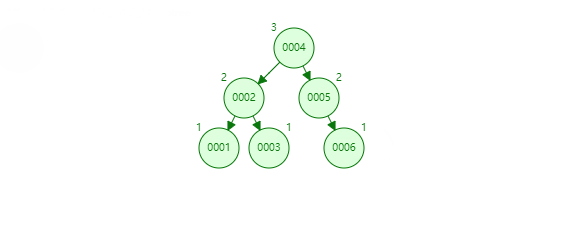
2.4 紅黑樹高度過高，磁碟IO次數頻繁

有沒有一種資料結構，即能夠快速查詢資料，又不需要頻繁的調整以維持平衡呢？這時紅黑樹就閃亮登場了。

紅黑樹和其他二叉搜尋樹類似， 都是在進行插入和刪除操作時通過特定操作保持二叉查詢樹的性質，從而獲得較高的查詢效能。與之不同的是，紅黑樹的平衡性並不像平衡搜尋二叉樹一樣嚴格的同時，又能保證在， O(log n) 時間複雜度內做查詢和刪除。

紅黑樹通過改變節點的顏色，可以有效減少節點的移動次數，由於紅黑樹的實現比較複雜，本文不再展開，感興趣的小夥伴可以去深入學習。

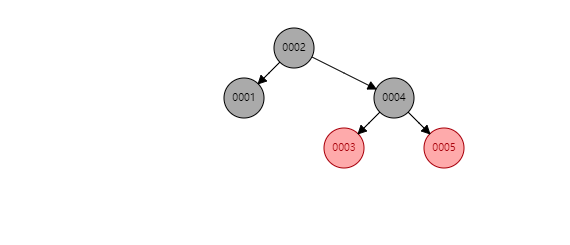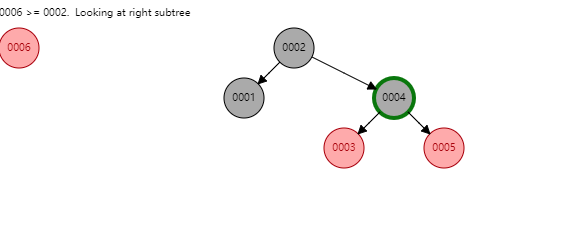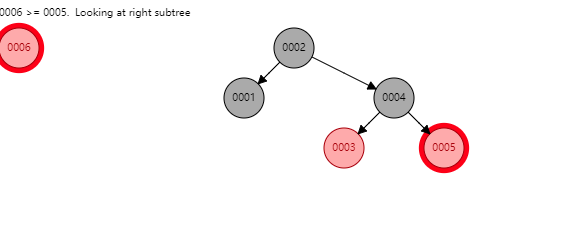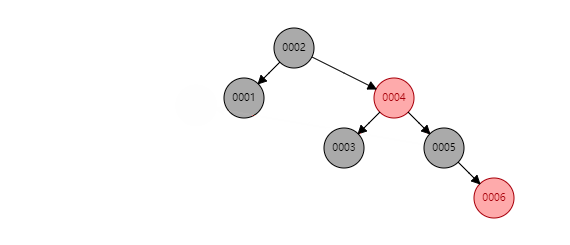
看似紅黑樹是一種完美的資料結構，能夠勝任索引的工作。但MySQL並未使用其作為索引的實現，主要原因在於紅黑樹的深度過大，資料檢索時造成磁碟IO頻繁，假設一個每個節點儲存在一個page中，樹的高度為10，則每次檢索可能就需要進行10次磁碟IO。

2.5 B-Tree不支援順序查詢

B-Tree是一種自平衡的多叉搜尋樹，一個節點可以擁有兩個以上的子節點。適合讀寫相對大的資料塊的儲存系統，例如磁碟。

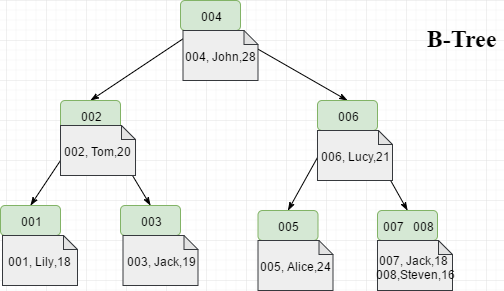
由於MySQL索引一般都儲存在記憶體中，如果使用B-Tree作為索引的話，索引和資料儲存在一塊，分佈在各個節點中；而記憶體資源往往比較寶貴，一定記憶體的情況下可以儲存的索引數量相對有限，畢竟每條資料的大小一般遠大於索引列的大小，導致記憶體使用率不高。

資料查詢過程中往往會有順序查詢，而B-Tree和紅黑樹對於順序查詢並不友好。

2.6 為什麼選B+Tree

B+Tree是在B-Tree基礎上演進而來的。與之不同的是B+Tree的資料頁只儲存在葉子節點中，並且葉子節點之間通過指標相連，為雙向連結串列結構。

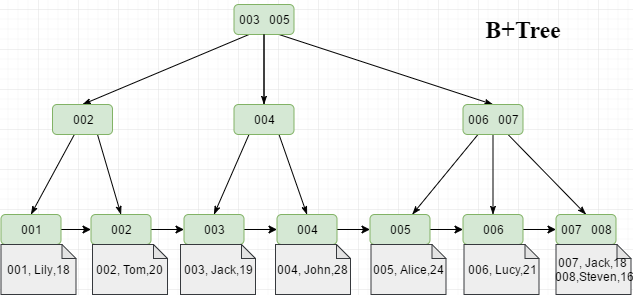
B+Tree的優點可以分為以四個：

1. 充分利用空間區域性性原理，適合磁碟儲存。

2. 樹的高度很低，能夠在儲存大量資料情況下，進行較少的磁碟IO【見下文介紹】。

3. 能夠很好支援單值，範圍查詢，有序性查詢。

4. 索引和資料分開儲存，讓更多的索引儲存在記憶體中。

三，MySQL中索引實現

3.1 巧妙利用B+Tree

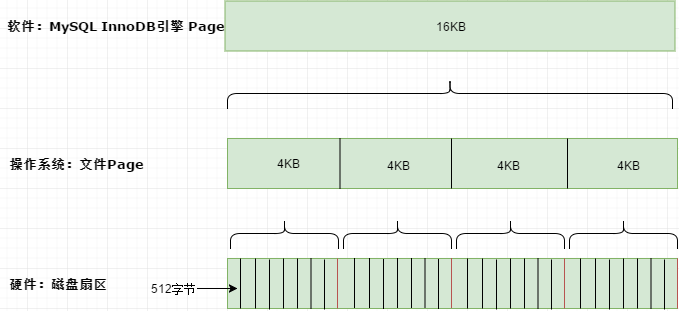
MySQL中的資料儲存通常以Page為單位，俗稱資料頁，每個Page對應B+Tree的一個節點。頁是InnoDB磁碟管理的最小單位，預設每個資料頁的大小為16kb，也可以通過引數innodb_page_size將頁的大小設定成其他值。

資料庫的頁大小和作業系統類似，是指存放資料時，每一塊連續區域資料的大小。比如一個1M的資料存放在資料庫中時， 需要大概64個頁來存放（1024=64*16）。如果是在作業系統上安裝的資料庫，最好將資料庫頁大小設定為作業系統頁大小的倍數，才是最佳設定。

3.2 樹的高度-有效減少磁碟IO次數

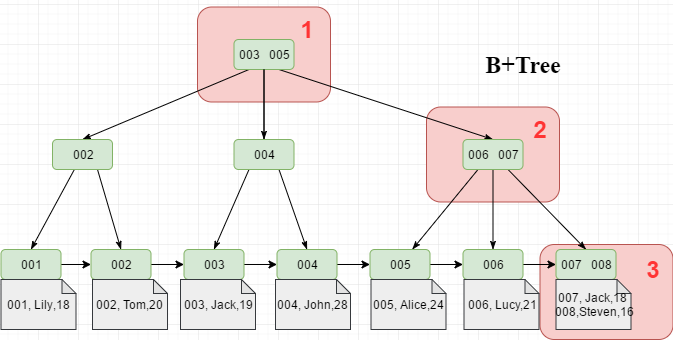
通常情況下，一張MySQL表中有成千上萬條資料，而磁碟IO次數往往與數的高度成正比。預設情況下一個Page的大小為16kb，由於每個Page中資料通過指標相連，且每個指標大小為6位元組。

在工作中，我們通常使用長度為8個位元組的bigint型別作為主鍵id的型別。已知，每一條資料都會包含一個6位元組的指標（資料頁中每條記錄都有指向下一條記錄的指標，但是沒有指向上一條記錄的指標）；所以一條索引資料大約佔用8+6=14個位元組，一個Page中能儲存16 * 1024 / 14 ≈ 1170條索引資料。高度為2的B+Tree大約能儲存1170*16 = 18720條這樣的記錄。同理，高度為3的B+Tree的B+Tree大約能儲存1170 * 1170 * 16 = 21902400，大約兩千萬條資料。 （每個節點大約能儲存1170條記錄，可以理解為此時B+Tree為1170叉樹）

例如，要檢索id=008的資料，則需要進行三次磁碟IO找到對應的資料頁（最多三次，因為Page可能在快取中），然後在資料頁中進行二分查詢，定位到對應的記錄。

四，總結

大家耳熟能詳的B+Tree索引是一種非常優秀的資料結構，也是面試熱點問題。本文從資料結構和磁碟IO兩個方面分析了為什麼使用B+Tree，以及MySQL的InnoDB儲存引擎的索引實現。在筆者面試過程中，被問到MySQL索引時通常也是從底層資料結構特點以及結合磁碟IO兩個角度去分析，屢試不爽。

學習一門技術時，我們不僅要知道其優點更要了解其缺點和瓶頸。在分析MySQL索引的實現時，不妨試試從其他資料結構的缺點入手！在Redis中使用跳錶實現了有序集合Zset，同樣支援高效的順序查詢，對比MySQL索引實現，跳錶能否替換B+Tree？如果不行，是因為什麼呢？