今天是2020年2月24日星期一。一個又一個意外因素串連起2020這不平凡的一年，多麼希望時間能夠倒退。曾經覺得電視上科比的畫面多麼熟悉，現在全成了陌生和追憶。

GitHub：https://github.com/wangzycloud/statistical-learning-method

提升方法

引入

　　提升方法是一種常用的統計學習方法，還是比較容易理解的。在分類問題中，通過改變訓練樣本的權重，學習多個分類器，並將這些分類器進行線性組合，從而提高分類的效能。其實說白了，就是一個人幹不好的活，我讓兩個人幹；兩個人幹不好，那就三個人四個人都來幹。但是人多了不能像三個和尚那樣沒水喝，都不幹活。包工頭要採取一些措施，措施一：一個人幹活的時候，哪裡乾的不好？就讓第二個人補充在這個地方；兩個人幹活的時候，哪裡乾的不好？就讓第三個人補充在這個地方。措施二：這三四個人在同一個地方幹活，怎樣確定這個活的結果乾的好不好呢？有的人幹活細緻認真，自然對結果增益大；幹活粗糙的，對結果增益不多，因此需要有一種組合策略進行判斷。通過幾個人共同努力，就解決了一個人幹不好的事情。

　　接下來的內容，將按照書中順序，先介紹提升方法的思路和代表性的提升演算法AdaBoost；再從前向分步加法模型角度解釋AdaBoost；最後看一個具體例項—提升樹。

提升方法AdaBoost演算法

　　提升方法基於這樣一種思想：對於一個複雜的任務來說，將多個專家的判斷進行適當的綜合所得出的判斷，要比其中任何一個專家單獨的判斷好。實際上，就是“三個臭皮匠頂個諸葛亮“的道理。書中上來提到了兩個稍晦澀的概念“強可學習”、“弱可學習”，下文沒有繼續闡述這兩個概念，這裡簡單的複述一下。在概率近似正確學習的框架中（不懂），一個概念，如果存在一個多項式的學習演算法能夠學習它，並且正確率很高，那麼就稱這個概念是強可學習的；一個概念，如果存在一個多項式的學習演算法能夠學習它，學習的正確率僅比隨機猜測略好，那麼就稱這個概念是弱可學習的。這兩個概念之間的相互關係，被證明是等價的，也就是說在一定的學習框架下，一個概念是強可學習的充分必要條件是這個概念是弱可學習的。（模型效果好==》強可學習；模型效果差==》弱可學習；兩者有聯絡）

　　這樣一來，在學習的過程中如果已經發現了“弱學習演算法”，那麼能否將它提升為“強學習演算法”。我們知道，發現弱學習演算法通常要比發現強學習演算法容易得多，如何具體實施提升，是我們開發提升方法時所要解決的問題。

　　對於分類問題而言，給定一個訓練資料樣本集，求比較粗糙的分類規則（弱分類器）要比求精確的分類規則容易得多。提升方法就是從弱學習演算法出發，反覆學習，得到一系列弱分類器（又稱為基本分類器），然後組合這些弱分類器，構成一個強分類器。並且大多數的提升方法都是改變訓練資料的概率分佈（訓練資料的權值分佈），針對不同的訓練資料分佈呼叫弱學習演算法學習一系列弱分類器。可以理解為難分的資料加大權重，讓下一個弱分類器重點學習該資料。

　　這樣，對於提升方法來說，有兩個問題需要解決：一是在每一輪如何改變訓練資料的權值或概率分佈；二是如何將弱分類器組合成一個強分類器。我們接下來要學習的AdaBoost演算法，針對第一個問題，提高那些被前一輪分類器錯誤分類樣本的權值，而降低那些被正確分類樣本的權值。這樣一來，那些沒有得到正確分類的資料，由於其權重的加大而受到後一輪弱分類器的更多關注。於是，分類問題被一系列的弱分類器“分而治之”。針對第二個問題，AdaBoost採取加權多數表決的方法。具體的，加大分類誤差率小的弱分類器的權值，使其在表決中起較大的作用；減小分類誤差率大的弱分類器的權值，使其在表決中起到較小的作用。

AdaBoost演算法

　　這裡先簡單的羅列AdaBoost演算法過程，先趕完整體進度，後期編寫程式碼時再整理細節。

　　假設給定一個二類分類的訓練資料集

AdaBoost演算法各個步驟的說明：

　　步驟（1）假設訓練資料集具有均勻的權值分佈，即每個訓練樣本在基本分類器的學習中作用相同，這一假設保證第一步能夠在原始資料上學習基本分類器G1(x)。

　　步驟（2）AdaBoost反覆學習基本分類器，在每一輪m=1，2，…，M順次執行四步操作：

　　第a步，使用當前分佈Dm加權的訓練資料集，學習基本分類器Gm(x)；

　　第b步，計算基本分類器Gm(x)在加權訓練資料集上的分類誤差率。實際上，第m個分類器的分類誤差率，就是被分類器Gm(x)誤分類樣本的權值之和，這表明權重大的樣本起的作用更大一些。如果將其誤分類，則誤差率大大增加，從而進一步影響Gm(x)的係數；

　　第c步，從公式8.8中，可以看出em≤1/2時，αm≥0，並且αm隨著em的減小而增大，所以分類誤差率越小的基本分類器在最終分類器中的作用越大；

　　第d步，更新訓練資料的權值分佈為下一輪做準備。可以看到，誤分類樣本在下一輪學習中起更大的作用，不改變所給的訓練資料，而不斷改變訓練資料權值的分佈，使得訓練資料在基本分類器的學習中起不同的作用。

　　步驟（3）線性組合f(x)實現M個基本分類器的加權表決。係數αm表示了基本分類器Gm(x)的重要性，這裡所有αm之和並不為1。f(x)的符號決定例項x的類，f(x)的絕對值表示分類的確信度。

AdaBoost的例子

AdaBoost演算法的訓練誤差分析

　　該訓練誤差分析部分，用證明出來的定理形式，表明AdaBoost演算法的最基本性質就是能在學習過程中不斷減少訓練誤差。也就是“該演算法能夠降低在訓練資料集的分類誤差率”這件事用數學方式證明了。分別是AdaBoost訓練誤差上界定理8.1、二分類問題的AdaBoost訓練誤差上界定理8.2和推論8.1。

　　該定理說明，可以在每一輪選取適當的Gm使得Zm最小，從而使訓練誤差下降的最快。對於二分類問題，有定理8.2。

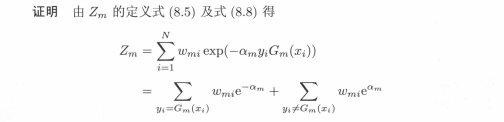
　　該推論表明，在此條件下，AdaBoost的訓練誤差是以指數速率下降的（看著像，不懂）。

AdaBoost演算法的解釋

　　本節內容從另外一個已經驗證的模型來分析AdaBoost演算法，並得到該演算法的另外解釋（我的理解是：AdaBoost演算法是一般化的加法模型的特例，現在要從加法模型的角度分析）。可以認為AdaBoost演算法是模型為加法模型、損失函式為指數函式、學習演算法為前向分佈演算法時的二類分類學習方法。接下來的內容，先對加法模型及前向分佈演算法做簡單介紹，通過對損失函式的分析，得到與AdaBoost演算法等價的引數表示。

　　考慮加法模型，b(x)函式相當於基分類器：

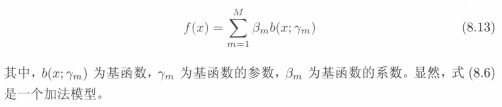
　　在給定訓練資料及損失函式L(y,f(x))的條件下，學習加法模型f(x)成為經驗風險極小化及損失函式極小化問題：

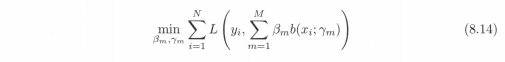
　　一般來說，加法模型f(x)中的M次基函式相加模型是一個複雜的優化問題，利用前向分佈演算法可以求解該優化問題。前向分佈演算法的思想是：因為學習的是加法模型，如果能夠從前向後，每一步只學習一個基函式及其係數，逐步逼近優化目標8.14，那麼就可以簡化優化的複雜度。具體的，每一步只需優化以下損失函式（相當於每一步優化一個基函式，優化一個前進一個）：

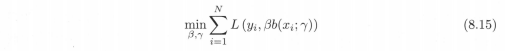
　　那麼，前向分佈演算法如下：

　　本來公式8.14中的同時求解從m=1到M所有引數β、γ的優化問題，通過前向分佈演算法簡化成了逐次求解各個β、γ的優化問題。

　　那麼，前向分佈演算法與AdaBoost演算法有什麼聯絡呢？我們可以用定理的形式敘述之間的聯絡，也就是我們可以由前向分佈演算法推匯出AdaBoost。定理如下：

　　以上內容直接截圖了。本是作為筆記進行整理，數學推導插不上解釋的嘴。要是以後文章被看到的多了，手推一下，再把內容整理上來。

提升樹

　　我們知道，提升方法實際上是採用加法模型（即基函式的線性組合）與前向分步演算法。本節提升樹是以決策樹作為基函式的提升方法，對分類問題決策樹是二叉分類樹，對迴歸問題決策樹是二叉迴歸樹。提升樹被認為是統計學習中效能最好的方法之一。

　　在例8.1中看到的基本分類器x<v或x>v，可以看作是一個根節點直接連線兩個葉節點的簡單決策樹，即所謂的決策樹樁。提升樹模型可以表示為決策樹的加法模型：

　　即使資料中的輸入與輸出之間的關係很複雜，樹的線性組合都可以很好地擬合訓練資料。分類問題與迴歸問題的區別主要在於使用的損失函式不同，迴歸問題中一般使用平方誤差損失函式，分類問題一般使用指數損失函式。對於二分類問題，提升樹演算法只需要將AdaBoost演算法8.1中的基本分類器限制為二類分類即可。下面看一下用於迴歸問題的提升樹：

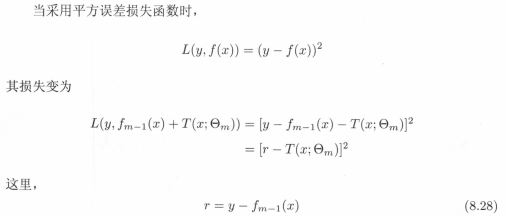
　　R是當前模型擬合數據的殘差，所以對迴歸問題的提升樹演算法來說，只需要簡單的擬合當前模型的殘差即可。具體演算法如下：

　　具體例子8.2：

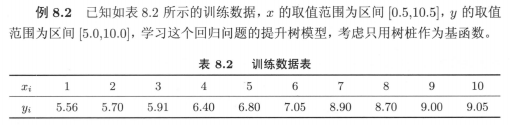
　　演算法8.1程式碼已上傳至github，先理解決策樹章節的演算法5.5，該提升樹會非常好理