文章目錄： [TOC] ## 1 任務 首先說下我們要搭建的網路要完成的學習任務： 讓我們的神經網路學會邏輯異或運算，異或運算也就是俗稱的“相同取0，不同取1” 。再把我們的需求說的簡單一點，也就是我們需要搭建這樣一個神經網路，讓我們在輸入（1,1）時輸出0，輸入（1,0）時輸出1（相同取0，不同取1），以此類推。 ## 2 實現思路 因為我們的需求需要有兩個輸入，一個輸出，所以我們需要在輸入層設定兩個輸入節點，輸出層設定一個輸出節點。因為問題比較簡單，所以隱含層我們只需要設定10個節點就可以達到不錯的效果了，隱含層的啟用函式我們採用ReLU函式，輸出層我們用Sigmoid函式，讓輸出保持在0到1的一個範圍，如果輸出大於0.5，即可讓輸出結果為1，小於0.5，讓輸出結果為0. ## 3 實現過程 我們使用的簡單的快速搭建法。 ### 3.1 引入必要庫 ```python import torch import torch.nn as nn import numpy as np ``` 用pytorch當然要引入torch包，然後為了寫程式碼方便將torch包裡的nn用nn來代替，nn這個包就是neural network的縮寫，專門用來搭神經網路的一個包。引入numpy是為了建立矩陣作為輸入。 ### 3.2 建立訓練集 ```python # 構建輸入集 x = np.mat('0 0;' '0 1;' '1 0;' '1 1') x = torch.tensor(x).float() y = np.mat('1;' '0;' '0;' '1') y = torch.tensor(y).float() ``` 我個人比較喜歡用np.mat這種方式構建矩陣，感覺寫法比較簡單，當然你也可以用其他的方法。但是構建完矩陣一定要有這一步```torch.tensor(x).float()```，必須要把你所建立的輸入轉換成tensor變數。 什麼是tensor呢？你可以簡單地理解他就是pytorch中用的一種變數，你想用pytorch這個框架就必須先把你的變數轉換成tensor變數。而我們這個神經網路會要求你的輸入和輸出必須是float浮點型的，指的是tensor變數中的浮點型，而你用np.mat建立的輸入是int型的，轉換成tensor也會自動地轉換成tensor的int型，所以要在後面加個.float（）轉換成浮點型。 這樣我們就構建完成了輸入和輸出（分別是x矩陣和y矩陣），x是四行二列的一個矩陣，他的每一行是一個輸入，一次輸入兩個值，這裡我們把所有的輸入情況都列了出來。輸出y是一個四行一列的矩陣，每一行都是一個輸出，對應x矩陣每一行的輸入。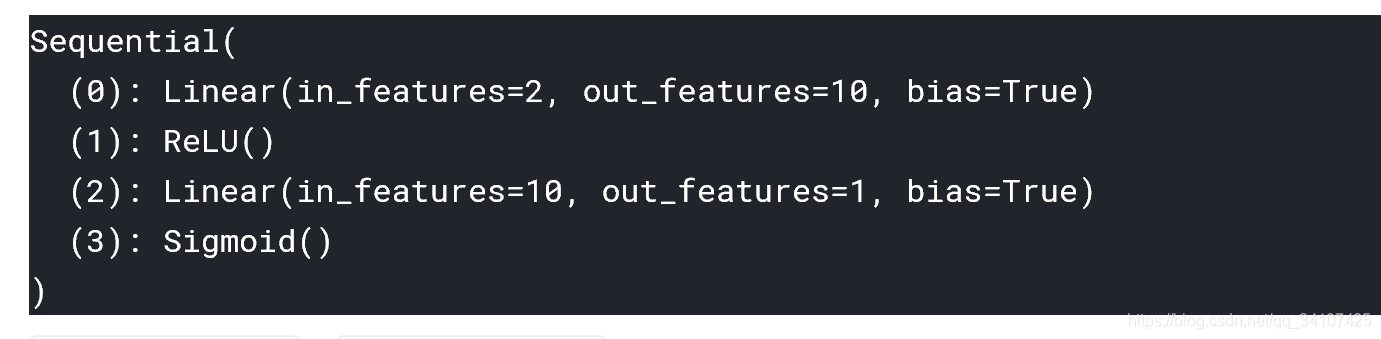 ### 3.3 搭建網路 ```python myNet = nn.Sequential( nn.Linear(2,10), nn.ReLU(), nn.Linear(10,1), nn.Sigmoid() ) print(myNet) ``` 輸出結果:  我們使用nn包中的Sequential搭建網路，這個函式就是那個可以讓我們像搭積木一樣搭神經網路的一個東西。 nn.Linear(2,10)的意思搭建輸入層，裡面的2代表輸入節點個數，10代表輸出節點個數。Linear也就是英文的線性，意思也就是這層不包括任何其它的啟用函式，你輸入了啥他就給你輸出了啥。nn.ReLU（）這個就代表把一個啟用函式層，把你剛才的輸入扔到了ReLU函式中去。 接著又來了一個Linear，最後再扔到Sigmoid函式中去。 2,10,1就分別代表了三個層的個數，簡單明瞭。 ### 3.4 設定優化器 ```python optimzer = torch.optim.SGD(myNet.parameters(),lr=0.05) loss_func = nn.MSELoss() ``` 對這一步的理解就是，你需要有一個優化的方法來訓練你的網路，所以這步設定了我們所要採用的優化方法。 torch.optim.SGD的意思就是採用SGD(隨機梯度下降)方法訓練，你只需要把你網路的引數和學習率傳進去就可以了，分別是```myNet.paramets```和```lr```。 ```loss_func```這句設定了代價函式，因為我們的這個問題比較簡單，所以採用了MSE，也就是均方誤差代價函式。 ### 3.5 訓練網路 ```python for epoch in range(5000): out = myNet(x) loss = loss_func(out,y) optimzer.zero_grad() loss.backward() optimzer.step() ``` 我這裡設定了一個5000次的迴圈（可能不需要這麼多次），讓這個訓練的動作迭代5000次。每一次的輸出直接用myNet（x），把輸入扔進你的網路就得到了輸出out（就是這麼簡單粗暴！），然後用代價函式和你的標準輸出y求誤差。 清除梯度的那一步是為了每一次重新迭代時清除上一次所求出的梯度，你就把這一步記住就行，初學不用理解太深。 ```loss.backward（）```當然就是讓誤差反向傳播，接著```optimzer.step（）```也就是讓我們剛剛設定的優化器開始工作。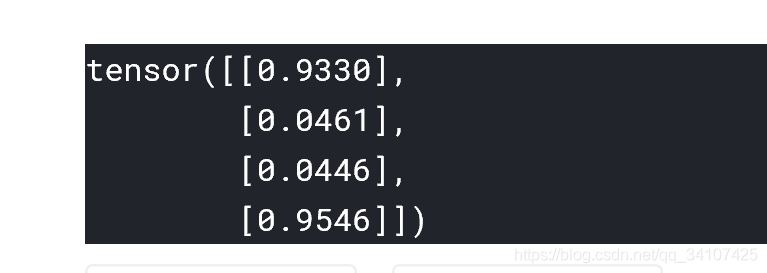 ### 3.6 測試 ```python print(myNet(x).data) ``` 執行結果:  可以看到這個結果已經非常接近我們期待的結果了，當然你也可以換個資料測試，結果也會是相似的。這裡簡單解釋下為什麼我們的程式碼末尾加上了一個.data，因為我們的tensor變數其實是包含兩個部分的，一部分是tensor資料，另一部分是tensor的自動求導引數，我們加上.data意思是輸出取tensor中的資料，如果不加的話會輸出下面這樣： ![在這裡插入圖片描述](https://img-blog.csdnimg.cn/20200128052757705.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM0MTA3NDI1,size_16,color_FFFFF