機器學習--線性單元迴歸--單變數梯度下降的實現
阿新 • • 發佈:2020-10-08
## 機器學習--線性單元迴歸--單變數梯度下降的實現
### 【線性迴歸】
```text
如果要用一句話來解釋線性迴歸是什麼的話,那麼我的理解是這樣子的:
**線性迴歸,是從大量的資料中找出最優的線性(y=ax+b)擬合函式,通過資料確定函式中的未知引數,進而進行後續操作(預測)
**迴歸的概念是從統計學的角度得出的,用抽樣資料去預估整體(迴歸中,是通過資料去確定引數),然後再從確定的函式去預測樣本。
```
### 【損失函式】
用線性函式去擬合數據,那麼問題來了,到底什麼樣子的函式最能表現樣本?對於這個問題,自然而然便引出了**損失函式**的概念,損失函式是一個用來評價樣本資料與目標函式(此處為線性函式)擬合程度的一個指標。我們假設,線性函式模型為:
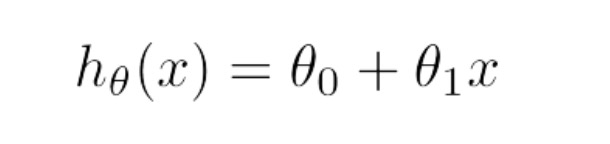
基於此函式模型,我們定義**損失函式**為:
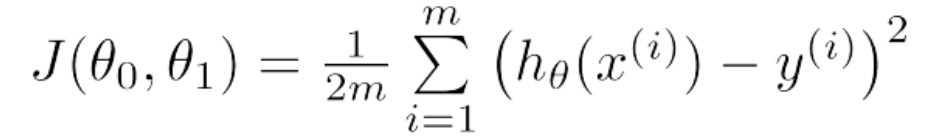
從上式中我們不難看出,損失函式是一個累加和(統計量)用來記錄預測值與真實值之間的1/2方差,從方差的概念我們知道,方差越小說明擬合的越好。那麼此問題進而演變稱為求解損失函式最小值的問題,因為我們要通過樣本來確定線性函式的中的引數θ_0和θ_1.
### 【梯度下降】
梯度下降演算法是求解最小值的一種方法,但並不是唯一的方法。梯度下降法的核心思想就是對損失函式求偏導,從隨機值(任一初始值)開始,沿著梯度下降的方向對`θ_0`和`θ_1`的迭代,最終確定`θ_0`和`θ_1`的值,注意,這裡要同時迭代`θ_0`和`θ_1`(這一點在程式設計過程中很重要),具體迭代過程如下: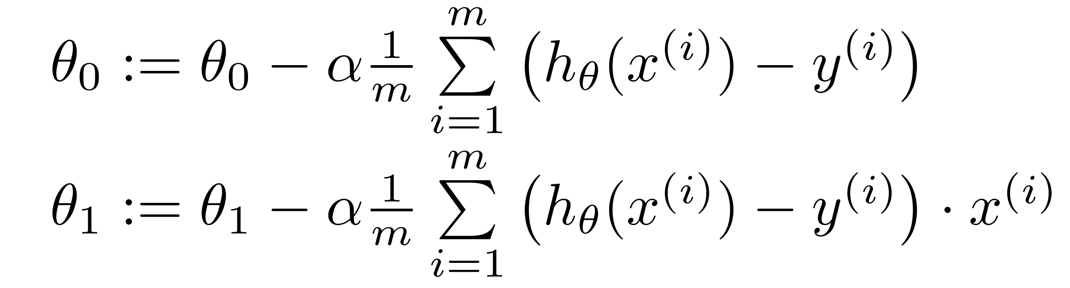
### 【Python程式碼實現】
那麼下面我們使用python程式碼來實現線性迴歸的梯度下降。
```python
#此處資料集,採用吳恩達第一次作業的資料集:ex1data1.txt
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
# 讀取資料
def readData(path):
data = np.loadtxt(path, dtype=float, delimiter=',')
return data
# 損失函式,返回損失函式計算結果
def costFunction(theta_0, theta_1, x, y, m):
predictValue = theta_0 + theta_1 * x
return sum((predictValue - y) ** 2) / (2 * m)
# 梯度下降演算法
# data:資料
# theta_0、theta_1:引數θ_0、θ_1
# iterations:迭代次數
# alpha:步長(學習率)
def gradientDescent(data, theta_0, theta_1, iterations, alpha):
eachIterationValue = np.zeros((iterations, 1))
x = data[:, 0]
y = data[:, 1]
m = data.shape[0]
for i in range(0, iterations):
hypothesis = theta_0 + theta_1 * x
temp_0 = theta_0 - alpha * ((1 / m) * sum(hypothesis - y))
temp_1 = theta_1 - alpha * (1 / m) * sum((hypothesis - y) * x)
theta_0 = temp_0
theta_1 = temp_1
costFunction_temp = costFunction(theta_0, theta_1, x, y, m)
eachIterationValue[i, 0] = costFunction_temp
return theta_0, theta_1, eachIterationValue
if __name__ == '__main__':
data = readData('ex1data1.txt')
iterations = 1500
plt.scatter(data[:, 0], data[:, 1], color='g', s=20)
# plt.show()
theta_0, theta_1, eachIterationValue = gradientDescent(data, 0, 0, iterations, 0.01)
hypothesis = theta_0 + theta_1 * data[:, 0]
plt.plot(data[:, 0], hypothesis)
plt.title("Fittingcurve")
plt.show()
plt.plot(np.arange(iterations),eachIterationValue)
plt.title('CostFunction')
plt.show()
# 在這裡我們使用向量的知識來寫程式碼
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
"""
1.獲取資料,並且將資料變為我們可以方便使用的資料格式
"""
def LoadFile(filename):
data = np.loadtxt(filename, delimiter=',', unpack=True, usecols=(0, 1))
X = np.transpose(np.array(data[:-1]))
y = np.transpose(np.array(data[-1:]))
X = np.insert(X, 0, 1, axis=1)
m = y.size
return X, y, m
"""
定義線性關係:Linear hypothesis function
"""
def h(theta, X):
return np.dot(X, theta)
"""
定義CostFunction
"""
def CostFunction(theta, X, y, m):
return float((1. / (2 * m)) * np.dot((h(theta, X) - y).T, (h(theta, X) - y)))
iterations = 1500
alpha = 0.01
def descendGradient(X, y, m, theta_start=np.array(2)):
theta = theta_start
CostVector = []
theta_history = []
for i in range(0, iterations):
tmptheta = theta
CostVector.append(CostFunction(theta, X, y, m))
theta_history.append(list(theta[:, 0]))
# 同步更新每一個theta的值
for j in range(len(tmptheta)):
tmptheta[j] = theta[j] - (alpha / m) * np.sum((h(theta, X) - y) * np.array(X[:, j]).reshape(m, 1))
theta = tmptheta
return theta, theta_history, CostVector
if __name__ == '__main__':
X, y, m = LoadFile('ex1data1.txt')
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 1], y[:, 0], color='red')
theta = np.zeros((X.shape[1], 1))
theta, theta_history, CostVector = descendGradient(X, y, m, theta)
predictValue = h(theta, X)
plt.plot(X[:, 1], predictValue)
plt.xlabel('the value of x')
plt.ylabel('the value of y')
plt.title('the liner gradient descend')
plt.show()
plt.plot(range(len(CostVector)), CostVector, 'bo')
plt.grid(True)
plt.title("Convergence of Cost Function")
plt.xlabel("Iteration number")
plt.ylabel("Cost function")
plt.xlim([-0.05 * iterations, 1.05 * iterations])
plt.ylim([4, 7])
plt.title('CostFunction')
plt.show()
# 我們使用我們寫好的線性模型去預測未知資料的情況,這樣我們就可以得出一個屬於我們自己的結果。
# 把我們線性模型預測的結果和實際的結果作一個對比,我們就可以看出實際結果是否真假性。
X, y, m = LoadFile('ex1data3.txt')
predictValue = h(theta, X)
print(predictValue)
# 這裡我們可以得到我們的預測值,我們用建立好的模型去預測未知的模型情況。
‘’‘
[[1.16037866]
[3.98169165]]
’‘’
```
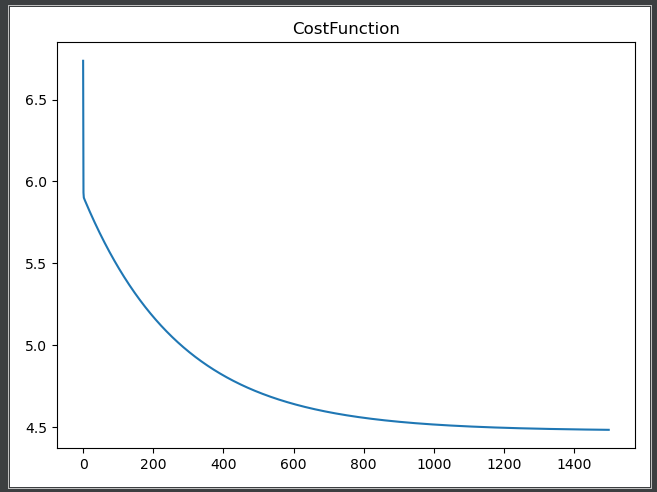
專案執行的結果為:
| 
|
| -------------------------------------------------------- |
| 
|
### 機器學習--多元線性迴歸--多變數梯度下降的實現
| 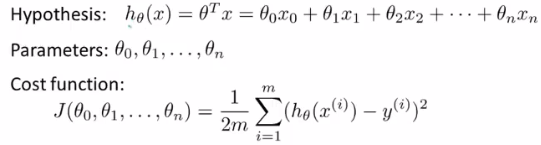
|
| -------------------------------------------------------- |
| 
|
| 
|
### 梯度下降--特徵縮放
通過特徵縮放這個簡單的方法,你將可以使得梯度下降的速度變得更快,收斂所迭代的次數變得更少。我們來看一下特徵縮放的含義。
```python
#Feature normalizing the columns (subtract mean, divide by standard deviation)
#Store the mean and std for later use
#Note don't modify the original X matrix, use a copy
stored_feature_means, stored_feature_stds = [], []
Xnorm = X.copy()
for icol in range(Xnorm.shape[1]):
stored_feature_means.append(np.mean(Xnorm[:,icol]))
stored_feature_stds.append(np.std(Xnorm[:,icol]))
#Skip the first column
if not icol: continue
#Faster to not recompute the mean and std again, just used stored values
Xnorm[:,icol] = (Xnorm[:,icol] - stored_feature_means[-1])/stored_feature_stds[-1]
```
### 學習率(alpha)
梯度下降的時候,我們有一個很重要的概念就是學習率的設定,在這裡我們要明確一個概念,學習率可以反映梯度下降的情況。如果學習率太低,我們梯度下降的速率就會很慢。同時如果學習率太高,我們的梯度下降會錯過最低點,theta的值不是最佳的,同時,可能不會收斂,一直梯度下去,值會越來越大。
那麼我們應該選擇一個多少大小的學習率是比較合適的呢?這裡吳恩達老師給了一個建議,我們不妨參考。
......0.01、0.03、006、009、0.1、0.3、0.6......。綜上所述,我們應該選擇一個合適大小的學習率。
### 特徵和多項式迴歸
| 
|
| ------------------------------------------------------------ |
| |
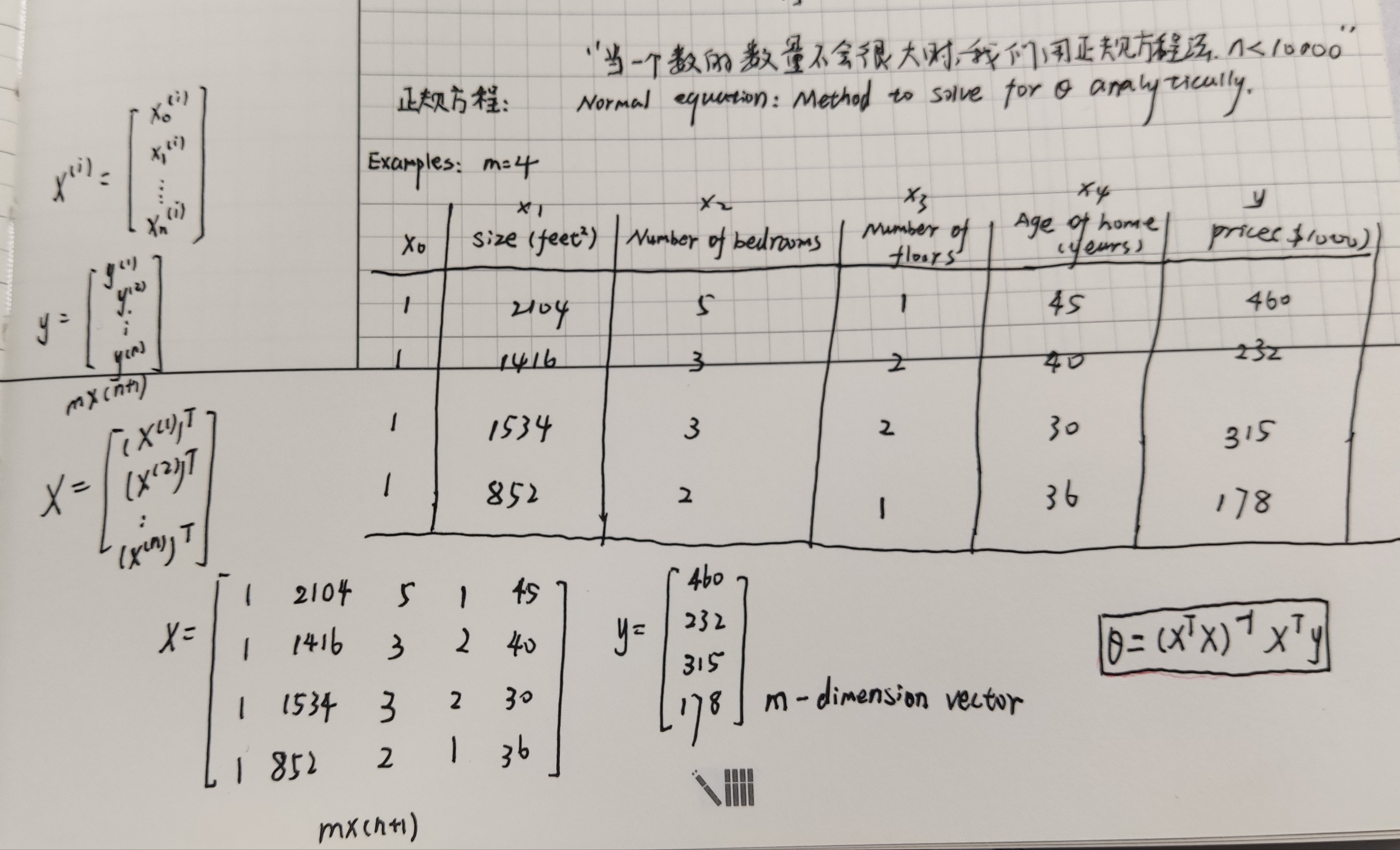
### 正規方程法(區別與迭代方法的直接求解)
| 
|
| ------------------------------------------------------------ |
| |
### 【Python程式碼實現多元的線性迴歸】
```python
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
"""
1.獲取資料的結果,使得資料是我們可以更好處理的資料
"""
def LoadFile(filename):
data = np.loadtxt(filename, delimiter=',', usecols=(0, 1, 2), unpack=True)
X = np.transpose(np.array(data[:-1]))
y = np.transpose(np.array(data[-1:]))
X = np.insert(X, 0, 1, axis=1)
m = y.shape[0]
return X, y, m
"""
2.構建線性函式
"""
def h(theta, X):
return np.dot(X, theta)
"""
3.損失函式CostFunction
"""
def CostFunction(X, y, theta, m):
return float((1. / (2 * m)) * np.dot((h(theta, X) - y).T, (h(theta, X) - y)))
"""
4.定義特徵縮放的函式
因為資料集之間的差別比較的大,所以我們這裡用可梯度下降--特徵縮放
"""
def normal_feature(Xnorm):
stored_feature_means, stored_feature_stds = [], []
for icol in range(Xnorm.shape[1]):
# 求平均值
stored_feature_means.append(np.mean(Xnorm[:, icol]))
# 求方差
stored_feature_stds.append(np.std(Xnorm[:, icol]))
# Skip the first column
if not icol: continue
# Faster to not recompute the mean and std again, just used stored values
Xnorm[:, icol] = (Xnorm[:, icol] - stored_feature_means[-1]) / stored_feature_stds[-1]
return Xnorm, stored_feature_means, stored_feature_stds
"""
5.定義梯度下降函式
"""
iterations = 1500
alpha = 0.01
def descendGradient(X, y, m, theta):
CostVector = []
theta_history = []
for i in range(iterations):
tmptheta = theta
theta_history.append(list(theta[:, 0]))
CostVector.append(CostFunction(X, y, theta, m))
for j in range(len(tmptheta)):
tmptheta[j, 0] = theta[j] - (alpha / m) * np.sum((h(theta, X) - y) * np.array(X[:, j]).reshape(m, 1))
theta = tmptheta
return theta, theta_history, CostVector
"""
6.定義繪圖函式
"""
def plotConvergence(jvec):
plt.figure(figsize=(10, 6))
plt.plot(range(len(jvec)), jvec, 'bo')
plt.grid(True)
plt.title("Convergence of Cost Function")
plt.xlabel("Iteration number")
plt.ylabel("Cost function")
plt.xlim([-0.05 * iterations, 1.05 * iterations])
plt.ylim([4, 7])
plt.show()
if __name__ == '__main__':
X, y, m = LoadFile('ex1data2.txt')
plt.figure(figsize=(10, 6))
plt.grid(True)
plt.xlim([-100, 5000])
plt.hist(X[:, 0], label='col1')
plt.hist(X[:, 1], label='col2')
plt.hist(X[:, 2], label='col3')
plt.title('Clearly we need feature normalization.')
plt.xlabel('Column Value')
plt.ylabel('Counts')
plt.legend()
plt.show()
Xnorm = X.copy()
Xnorm, stored_feature_means, stored_feature_stds = normal_feature(Xnorm)
plt.grid(True)
plt.xlim([-5, 5])
plt.hist(Xnorm[:, 0], label='col1')
plt.hist(Xnorm[:, 1], label='col2')
plt.hist(Xnorm[:, 2], label='col3')
plt.title('Feature Normalization Accomplished')
plt.xlabel('Column Value')
plt.ylabel('Counts')
plt.legend()
plt.show()
theta = np.zeros((Xnorm.shape[1], 1))
theta, theta_history, CostVector = descendGradient(Xnorm, y, m, theta)
plotConvergence(CostVector)
print("Check of result: What is price of house with 1650 square feet and 3 bedrooms?")
ytest = np.array([1650., 3.])
# To "undo" feature normalization, we "undo" 1650 and 3, then plug it into our hypothesis
# 對於每次傳來的一個數字我們讀進行適當的特徵縮放的功能
ytestscaled = [(ytest[x] - stored_feature_means[x + 1]) / stored_feature_stds[x + 1] for x in range(len(ytest))]
ytestscaled.insert(0, 1)
print(ytestscaled)
# 預測未知的值,通過我們已經建立好的模型來預測未知的值。
print("$%0.2f" % float(h(theta, ytestscaled)))
# 輸出的結果為:
[1, -0.4460438603276164, -0.2260933675776883]
$293098.15
輸出的截圖這裡就不截圖了
```
### 【python程式碼實現一元和多元線性迴歸彙總】
```python
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
cols = np.loadtxt(datafile,delimiter=',',usecols=(0,1),unpack=True) #Read in comma separated data
#Form the usual "X" matrix and "y" vector
X = np.transpose(np.array(cols[:-1]))
y = np.transpose(np.array(cols[-1:]))
m = y.size # number of training examples
#Insert the usual column of 1's into the "X" matrix
X = np.insert(X,0,1,axis=1)
print(X)
#Plot the data to see what it looks like
plt.figure(figsize=(10,6))
plt.plot(X[:,1],y[:,0],'rx',markersize=10)
plt.grid(True) #Always plot.grid true!
plt.ylabel('Profit in $10,000s')
plt.xlabel('Population of City in 10,000s')
iterations = 1500
alpha = 0.01
def h(theta,X): #Linear hypothesis function
return np.dot(X,theta)
def computeCost(mytheta,X,y): #Cost function
"""
theta_start is an n- dimensional vector of initial theta guess
X is matrix with n- columns and m- rows
y is a matrix with m- rows and 1 column
"""
#note to self: *.shape is (rows, columns)
return float((1./(2*m)) * np.dot((h(mytheta,X)-y).T,(h(mytheta,X)-y)))
#Test that running computeCost with 0's as theta returns 32.07:
initial_theta = np.zeros((X.shape[1],1)) #(theta is a vector with n rows and 1 columns (if X has n features) )
print(computeCost(initial_theta,X,y))
#Actual gradient descent minimizing routine
def descendGradient(X, theta_start = np.zeros(2)):
"""
theta_start is an n- dimensional vector of initial theta guess
X is matrix with n- columns and m- rows
"""
theta = theta_start
jvec = [] #Used to plot cost as function of iteration
thetahistory = [] #Used to visualize the minimization path later on
for meaninglessvariable in range(iterations):
tmptheta = theta
jvec.append(computeCost(theta,X,y))
# Buggy line
#thetahistory.append(list(tmptheta))
# Fixed line
thetahistory.append(list(theta[:,0]))
#Simultaneously updating theta values
for j in range(len(tmptheta)):
tmptheta[j] = theta[j] - (alpha/m)*np.sum((h(initial_theta,X) - y)*np.array(X[:,j]).reshape(m,1))
theta = tmptheta
return theta, thetahistory, jvec
#Actually run gradient descent to get the best-fit theta values
initial_theta = np.zeros((X.shape[1],1))
theta, thetahistory, jvec = descendGradient(X,initial_theta)
#Plot the convergence of the cost function
def plotConvergence(jvec):
plt.figure(figsize=(10,6))
plt.plot(range(len(jvec)),jvec,'bo')
plt.grid(True)
plt.title("Convergence of Cost Function")
plt.xlabel("Iteration number")
plt.ylabel("Cost function")
dummy = plt.xlim([-0.05*iterations,1.05*iterations])
#dummy = plt.ylim([4,8])
plotConvergence(jvec)
dummy = plt.ylim([4,7])
#Plot the line on top of the data to ensure it looks correct
def myfit(xval):
return theta[0] + theta[1]*xval
plt.figure(figsize=(10,6))
plt.plot(X[:,1],y[:,0],'rx',markersize=10,label='Training Data')
plt.plot(X[:,1],myfit(X[:,1]),'b-',label = 'Hypothesis: h(x) = %0.2f + %0.2fx'%(theta[0],theta[1]))
plt.grid(True) #Always plot.grid true!
plt.ylabel('Profit in $10,000s')
plt.xlabel('Population of City in 10,000s')
plt.legend()
#Import necessary matplotlib tools for 3d plots
from mpl_toolkits.mplot3d import axes3d, Axes3D
from matplotlib import cm
import itertools
fig = plt.figure(figsize=(12,12))
ax = fig.gca(projection='3d')
xvals = np.arange(-10,10,.5)
yvals = np.arange(-1,4,.1)
myxs, myys, myzs = [], [], []
for david in xvals:
for kaleko in yvals:
myxs.append(david)
myys.append(kaleko)
myzs.append(computeCost(np.array([[david], [kaleko]]),X,y))
scat = ax.scatter(myxs,myys,myzs,c=np.abs(myzs),cmap=plt.get_cmap('YlOrRd'))
plt.xlabel(r'$\theta_0$',fontsize=30)
plt.ylabel(r'$\theta_1$',fontsize=30)
plt.title('Cost (Minimization Path Shown in Blue)',fontsize=30)
plt.plot([x[0] for x in thetahistory],[x[1] for x in thetahistory],jvec,'bo-')
plt.show()
datafile = 'data/ex1data2.txt'
#Read into the data file
cols = np.loadtxt(datafile,delimiter=',',usecols=(0,1,2),unpack=True) #Read in comma separated data
#Form the usual "X" matrix and "y" vector
X = np.transpose(np.array(cols[:-1]))
y = np.transpose(np.array(cols[-1:]))
m = y.size # number of training examples
#Insert the usual column of 1's into the "X" matrix
X = np.insert(X,0,1,axis=1)
#Quick visualize data
plt.grid(True)
plt.xlim([-100,5000])
dummy = plt.hist(X[:,0],label = 'col1')
dummy = plt.hist(X[:,1],label = 'col2')
dummy = plt.hist(X[:,2],label = 'col3')
plt.title('Clearly we need feature normalization.')
plt.xlabel('Column Value')
plt.ylabel('Counts')
dummy = plt.legend()
#Feature normalizing the columns (subtract mean, divide by standard deviation)
#Store the mean and std for later use
#Note don't modify the original X matrix, use a copy
stored_feature_means, stored_feature_stds = [], []
Xnorm = X.copy()
for icol in range(Xnorm.shape[1]):
stored_feature_means.append(np.mean(Xnorm[:,icol]))
stored_feature_stds.append(np.std(Xnorm[:,icol]))
#Skip the first column
if not icol: continue
#Faster to not recompute the mean and std again, just used stored values
Xnorm[:,icol] = (Xnorm[:,icol] - stored_feature_means[-1])/stored_feature_stds[-1]
#Quick visualize the feature-normalized data
plt.grid(True)
plt.xlim([-5,5])
dummy = plt.hist(Xnorm[:,0],label = 'col1')
dummy = plt.hist(Xnorm[:,1],label = 'col2')
dummy = plt.hist(Xnorm[:,2],label = 'col3')
plt.title('Feature Normalization Accomplished')
plt.xlabel('Column Value')
plt.ylabel('Counts')
dummy = plt.legend()
#Run gradient descent with multiple variables, initial theta still set to zeros
#(Note! This doesn't work unless we feature normalize! "overflow encountered in multiply")
initial_theta = np.zeros((Xnorm.shape[1],1))
theta, thetahistory, jvec = descendGradient(Xnorm,initial_theta)
#Plot convergence of cost function:
plotConvergence(jvec)
#print "Final result theta parameters: \n",theta
print ("Check of result: What is price of house with 1650 square feet and 3 bedrooms?")
ytest = np.array([1650.,3.])
#To "undo" feature normalization, we "undo" 1650 and 3, then plug it into our hypothesis
# 對於每次傳來的一個數字我們讀進行適當的特徵縮放的功能
ytestscaled = [(ytest[x]-stored_feature_means[x+1])/stored_feature_stds[x+1] for x in range(len(ytest))]
ytestscaled.insert(0,1)
print ("$%0.2f" % float(h(theta,ytestscaled)))
from numpy.linalg import inv
#Implementation of normal equation to find analytic solution to linear regression
def normEqtn(X,y):
#restheta = np.zeros((X.shape[1],1))
return np.dot(np.dot(inv(np.dot(X.T,X)),X.T),y)
print ("Normal equation prediction for price of house with 1650 square feet and 3 bedrooms")
print ("$%0.2f" % float(h(normEqtn(X,y),[1,1650.,3]
