樸素貝葉斯分類-理論篇
阿新 • • 發佈:2020-11-18
> **公號:碼農充電站pro**
> **主頁:https://codeshellme.github.io**
貝葉斯原理是英國數學家**托馬斯·貝葉斯**於18 世紀提出的,當我們不能直接計算一件事情(A)發生的可能性大小的時候,可以間接的計算與這件事情有關的事情(X,Y,Z)發生的可能性大小,從而間接判斷事情(A)發生的可能性大小。

在介紹貝葉斯原理之前,先介紹幾個與概率相關的概念。
### 1,概率相關概念
**概率**用於描述一件事情發生的可能性大小,用數學符號`P(x)` 表示,`x` 表示**隨機變數**,`P(x)` 表示`x` 的概率。
**隨機變數**根據變數取值是否連續,可分為**離散型隨機變數**和**連續型隨機變數**。
**聯合概率**由多個隨機變數共同決定,用`P(x, y)` 表示,含義為“事件`x` 與事件`y` 同時發生的概率”。
**條件概率**也是由多個隨機變數共同決定,用`P(x|y)` 表示,含義為“在事件`y` 發生的前提下,事件`x` 發生的概率。”
**邊緣概率**:從 `P(x, y)` 推匯出 `P(x)`,從而忽略 `y` 變數。
- 對於離散型隨機變數,通過聯合概率 `P(x, y)` 在 `y` 上**求和**, 可得到`P(x)`,這裡的`P(x)` 就是邊緣概率。
- 對於連續型隨機變數,通過聯合概率 `P(x, y)` 在 `y` 上**求積分**, 可得到`P(x)`,這裡的`P(x)` 就是邊緣概率。
**概率分佈**:將隨機變數所有可能出現的值,及其對應的概率都展現出來,就能得到這個變數的**概率分佈**,概率分佈分為兩種,分別是離散型和連續型。
常見的**離散型資料分佈模型**有:
- 伯努利分佈:表示單個隨機變數的分佈,且該變數的取值只有兩個,0 或 1。例如拋硬幣(不考慮硬幣直立的情況)的概率分佈就是伯努利分佈。數學公式如下:
- P(x = 0) = 1 - λ
- P(x = 1) = λ
- 多項式分佈:也叫分類分佈,描述了一個具有 k 個不同狀態的單個隨機變數。這裡的 k,是有限的數值,如果 k 為 2,那就變成了伯努利分佈。
- P(x = k) = λ
- 二項式分佈
- 泊松分佈
常見的**連續型資料分佈模型**有:
- 正態分佈,也叫高斯分佈,是最重要的一種。
- 均勻分佈
- 指數分佈
- 拉普拉斯分佈
正態分佈的數學公式為:

正態分佈的分佈圖為:
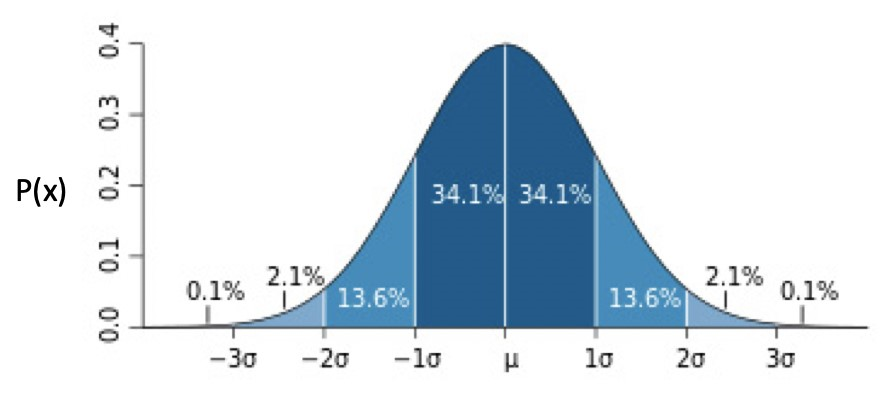
正態分佈還可分為:
- 一元正態分佈:此時 **μ**為 0,**σ**為 1。
- 多元正態分佈。
**數學期望**,如果把“每次隨機結果的出現概率”看做**權重**,那麼期望就是所有結果的**加權平均值**。
**方差**表示的是隨機變數的取值與其數學期望的偏離程度,方差越小意味著偏離程度越小,方差越大意味著偏離程度越大。
**概率論**研究的就是這些概率之間的轉化關係。
### 2,貝葉斯定理
貝葉斯公式如下:
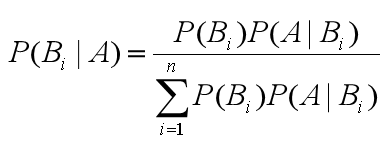
含義:
- 等號右邊分子部分,`P(Bi)` 為**先驗概率**,`P(A|Bi)` 為**條件概率**。
- 等號右邊整個分母部分為**邊緣概率**。
- 等號左邊`P(Bi|A)` 為**後驗概率**,由先驗概率,條件概率,邊緣概率計算得出。
貝葉斯定理可用於分類問題,將其用在分類問題中時,可將上面的公式簡化為:
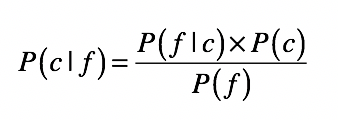
其中:
- c 表示一個分類,f 表示屬性值。
- P(c|f) 表示在待分類樣本中,出現屬性值 f 時,樣本屬於類別 c 的概率。
- P(f|c) 是根據訓練樣本資料,進行統計得到的,分類 c 中出現屬性 f 的概率。
- P(c ) 是分類 c 在訓練資料中出現的概率。
- P(f) 是屬性 f 在訓練樣本中出現的概率。
這就意味著,當我們知道一些屬性特徵值時,根據這個公式,就可以計算出所屬分類的概率,最終所屬哪個分類的概率最大,就劃分為哪個分類,這就完成了一個分類問題。
***貝葉斯推導***
來看下貝葉斯公式是如何推匯出來的。
如下圖兩個橢圓,左邊為C,右邊為F。
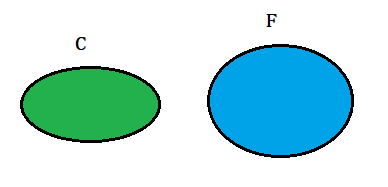
現在讓兩個橢圓產生交集:
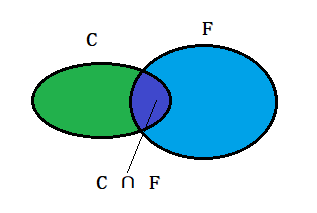
根據上圖可知:在事件F 發生的條件下,事件C 發生的概率就是`P(C ∩ F) / P(F)`,即:
- `P(C | F) = P(C ∩ F) / P(F)`
可得到:
- `P(C ∩ F) = P(C | F) * P(F)`
同理可得:
- `P(C ∩ F) = P(F | C) * P(C)`
所以:
- `P(C ∩ F) = P(C | F) * P(F) = P(F | C) * P(C)`
- `P(C | F) = P(F | C) * P(C) / P(F)`
### 3,樸素貝葉斯
假設我們現在有一個數據集,要使用貝葉斯定理,進行分類。特徵有兩個:f1,f2。現在要對資料`F` 進行分類,那我們需要求解:
- `P(c|F)`:表示資料`F` 屬於分類`c` 的概率。
因為特徵有 `f1` 與 `f2`,那麼:
- `P(c|F) = P(c|(f1,f2))`
對於分類問題,特徵往往不止一個。如果特徵之間相互影響,也就是`f1` 與`f2` 之間相互影響,那麼`P(c|(f1,f2))` 就不容易求解。
**樸素貝葉斯在貝葉斯的基礎上做了一個簡單粗暴的假設,它假設多個特徵之間互不影響,相互獨立。**
> **樸素**的意思就是**純樸,簡單**。
用數學公式表示就是:
- `P(A, B) = P(A) * P(B)`
實際上就是大學概率論中所講的**事件獨立性**,即**事件A 與事件B 的發生互不干擾,相互獨立**。
那麼,根據樸素貝葉斯,`P(c|F)` 的求解過程如下:
---
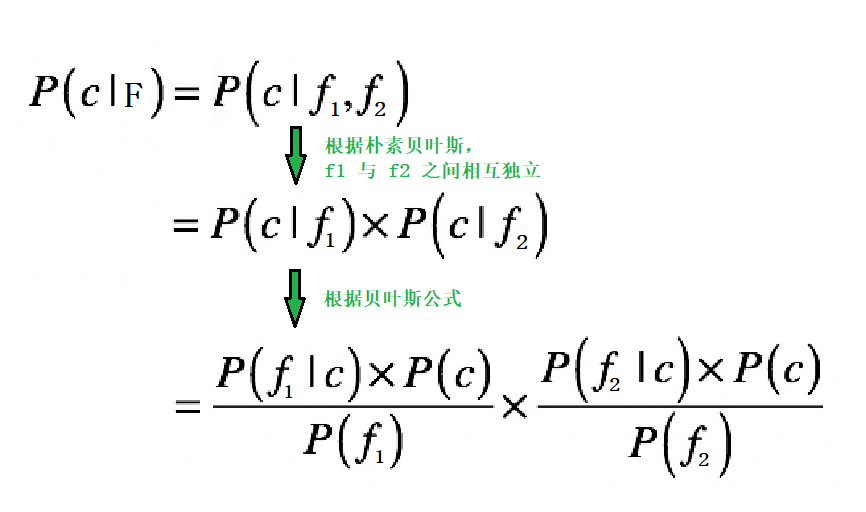
---
假設我們現在要分類的資料有兩類:`c1 和 c2`。
那麼對於資料`F` 的分類問題,我們就需要求解兩個概率:`P(c1|F) 和P(c2|F)`:
- 如果`P(c1|F) > P(c2|F)`,那麼`F` 屬於`c1` 類。
- 如果`P(c1|F) < P(c2|F)`,那麼`F` 屬於`c2` 類。
根據貝葉斯原理,我們可以得到:
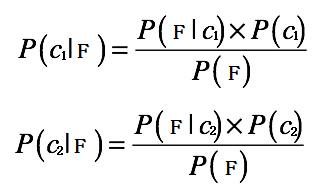
對於分類問題,我們的最終目的是分類,而不是真正的求解出`P(c1|F)` 和 `P(c2|F)` 的確切數值。
根據上面的公式,我們可以看到,等號右邊的分母部分都是`P(F)`:
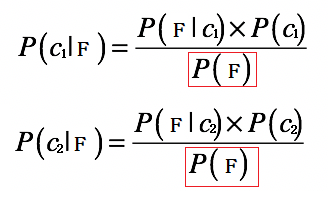
所以我們只需要求出`P(F|c1) × P(c1)` 和 `P(F|c2) × P(c2)`,就可以知道`P(c1|F)` 和 `P(c2|F)` 哪個大了。
所以對於`P(c|F)` 可以進一步簡化:
---

---
### 4,處理分類問題的一般步驟
用樸素貝葉斯原理,處理一個分類問題,一般要經過以下幾個步驟:
- **準備階段**:
- 獲取資料集。
- 分析資料,確定特徵屬性,並得到訓練樣本。
- **訓練階段**:
- 計算每個類別概率`P(Ci)`。
- 對每個特徵屬性,計算每個分類的條件概率`P(Fj|Ci)`。
- `Ci` 代表所有的類別。
- `Fj` 代表所有的特徵。
- **預測階段**:
- 給定一個數據,計算該資料所屬每個分類的概率`P(Fj|Ci) * P(Ci)`。
- 最終那個分類的概率大,資料就屬於哪個分類。
### 5,用樸素貝葉斯分類
接下來我們來處理一個實際的分類問題,我們處理的是**離散型資料**。
#### 5.1,準備資料集
我們的資料集如下:
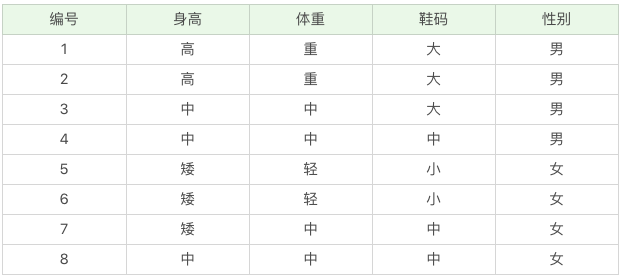
該資料集的特徵集有`身高`,`體重`和`鞋碼`,目標集為`性別`。
我們的目的是訓練一個模型,該模型可以根據身高,體重和鞋碼來預測所屬的性別。
我們給定一個特徵:
- 身高 = 高,用`F1` 表示。
- 體重 = 中,用`F2` 表示。
- 鞋碼 = 中,用`F3` 表示。
要求這個特徵是`男`還是`女`?(用`C1` 表示`男`,`C2` 表示`女`)也就是要求`P(C1|F)` 大,還是`P(C2|F)` 大?
```python
# 根據樸素貝葉斯推導
P(C1|F)
=>
