魔幻的 2020 讓我們懷疑人生是否存在最優解？我們某個時間的決策究竟是否正確？歷史不能改變，但卻會重演，我們究竟要從過去中學到什麼呢？ 讓我們一起從動態規劃中，來找尋這些問題的答案吧～ （咳咳，今天開始迴歸算法系列，來聊一聊之前的演算法文章中沒有講到的內容。 ## 什麼是動態規劃 動態規劃（Dynamic Programic，簡稱 DP）是一種求解最優解的方法，它是一種特殊的分治思想，利用它可以實現時間複雜度的優化，有時也可以進行空間複雜度的優化，有時是需要更多的空間的（相比其他方法）。 dynamic 是動態的意思，也就是變化的，programing 可以理解為方程（我瞎說的），結合起來就是動態規劃是用狀態轉移方程來求得最優解的演算法。 在解釋動態規劃的時候，我們順便理一理和它相關的兩種思想——分治和貪心演算法。 ### 分治 分治是把大問題分解成若干個子問題，這樣的能分解性質就是最優子結構的。 最簡單的例子就是小明在解決問題 A 的時候，發現問題 A 是由問題 B 和 C 一起組成的，所以他想要解決問題 A，就需要把 B、C 一起去解決。 ### 動態規劃 動態規劃是分治法的特例。 動態規劃比分治法多了一種，就是重疊的子問題。 什麼是重疊的子問題呢？舉個例子來講，可愛的小明遇到了一個可愛的問題，那就是問題 A，但是在前面需要解決一連串的問題，我們用`A1，A2，A3，A4 ... A`來表示，在解決`A1`之後會用它的解去解決類似的問題`A2`， 然後再去解決`A3`，最終再去解決 A，這就是重疊的子問題的典型代表。（下面的例題還會解釋這個概念） ### 貪心 貪心比動態規劃更加的特殊，它還需要問題滿足另外一個性質——貪心選擇性質，每次都可以把原問題分解成為一個子問題。 實際上再用動規的例子來說明貪心，在解決`A1，A2，A3，A4 ... A`的時候，他發現解決不光有一種重疊子問題的性質在裡面，更有趣的是，解決`A1`需要一種特殊的規則。 例如小明現在在玩電腦遊戲，而電腦遊戲的最終目的是到達`A`，而他又發現，只要一直往右邊走就能到達最終的目的地了。這就是一種貪心的演算法，在每次往右邊走，就是一種特殊的規則，而走到目的地`A`需要很多重複的子問題，也即每次活動一個單位。 ### 入門 其實在很久之前我寫的一篇文章中，以斐波那契數列這道基本題為例，詳細闡述了從遞迴到 DP 的優化方法和思路，以及簡單題的不簡單的答法，大家不妨先去複習一下： [這才是面試官想聽的：從遞迴到 DP 的優化](https://mp.weixin.qq.com/s/AOze7X3R2hdaDqhCybLIrw) 然後我們再來看看一般的動態規劃解題思路。 ## 解題思路 回到動態規劃，這裡有四個基本的概念： - state（狀態表示） - function（轉移方程） - initial（初始化） - final state（最終的狀態） 在剛開始的時候，我們首先需要構建一個儲存資料的表格，一般是陣列或者矩陣，然後設定好每一個格子到下一個格子需要的轉移方程。 然後去執行重複的步驟，從初始化的狀態一直計算到最終需要的狀態。 回到小明的例子，剛開始的時候小明需要確定一個 state（`A0`代表的是什麼），然後找到`A0`與`A1`之間的關係，從初始化開始一直計算到最終的狀態。 接下來，我們以 Leetcode 120 來詳細的講解這個演算法。 ## 題目描述  現在我們來分析一下這個題目，首先我們分析一下為什麼它是一個動態規劃的問題。 題目是要找到一種路徑的和，這種路徑和是要最小的，也就是求一個`最優解`。 因為這是路徑，我們就是在每一層裡面選擇一個合適的數字，然後連成一個路徑，在這道題目裡面，最小的路徑是`2-3-5-1`，在第一層挑了`2`，在第二層挑了`3`。也就是說總的問題拆分成了每一層的問題，而每一層之間都有一種依賴性在裡面，例如第二層選擇了`3`之後只能在`6,5`之中選擇一個，不能跳到`7`，這就是`重疊子問題`。 我們用`f[i][j]`表示從三角形頂部走到位置 `[i][j]` 的最小路徑和。這裡的位置 `i, j` 指的是三角形中第 i 行第 j 列的位置。 由於只能是從一個節點到相鄰的兩個節點（樹），因此要想走到位置 `[i][j]`，上一步就只能在位置 `[i-1][j-1]` 或者位置 `[i-1][j]`。 我們在這兩個位置中選擇一個路徑和較小的來進行轉移，狀態轉移方程為： `f[i][j]=min(f[i−1][j−1],f[i−1][j])+c[i][j]`， 其中 `c[i][j]` 指的是`triangle[i][j]`的數值。 ### 方法一 當設定完通項方程之後，我們還需要設定一些特殊的轉化方程： - 當靠近左邊界時，也就是 `j = 0` 時，於是沒有`f[i-1][j−1]`這一項 ，狀態轉移方程變為： `f[i][0]=f[i−1][0]+c[i][0]` - 當靠近右邊界時，我們直接用上一層斜上角位置的數值進行計算： `f[i][i]=f[i−1][i−1]+c[i][i]` 最終，我們只需要在 dp 三角形的最後一行找到最小值就可以了。 那麼初始的狀態是什麼呢？ 實際上就是剛開始的時候設定 dp 的第一個單位的數值為`cp[0][0]`，也即是`dp[0][0] = c[0][0]`。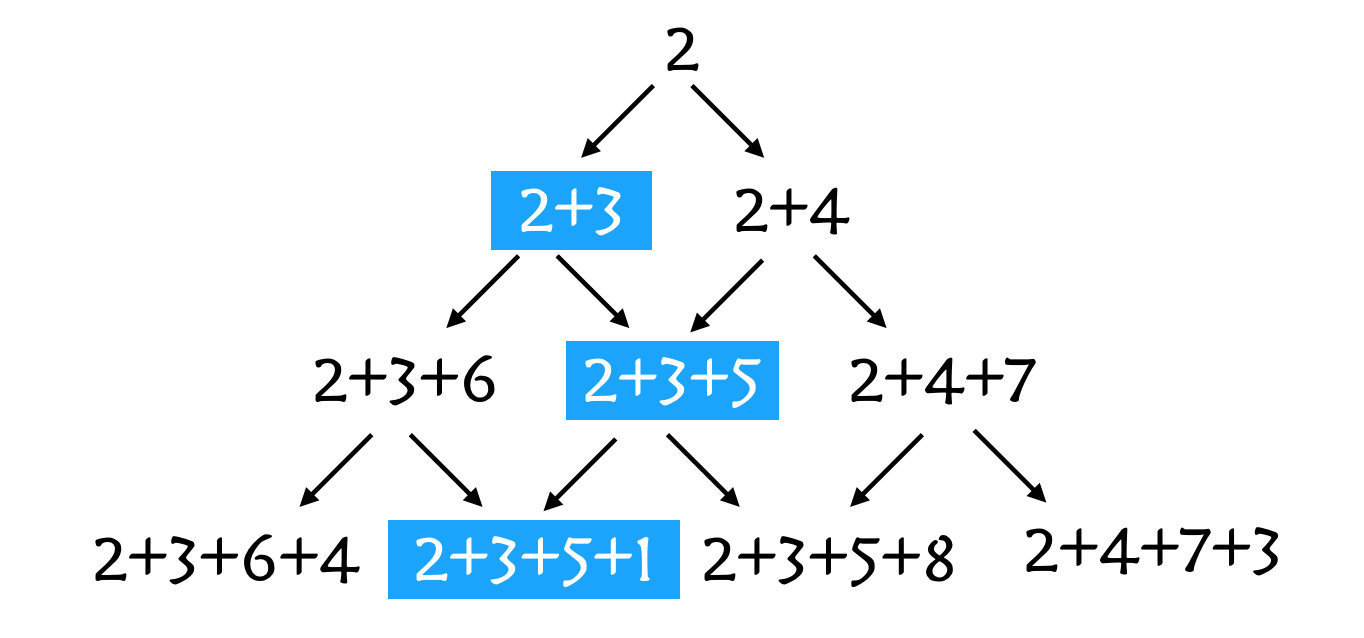 狀態轉換圖如下所示：  程式碼如下： ```java class Solution { public int minimumTotal(List> triangle) { // 建立表格 int[][] dp = new int[triangle.size()][triangle.size()]; dp[0][0] = triangle.get(0).get(0); // 動態規劃的方程式 for (int i = 1; i < dp.length; i++) { for (int j = 0; j <= i; j++) { int curr = triangle.get(i).get(j); if (j == 0) { dp[i][j] = dp[i-1][j] + curr; } else if (j == i) { dp[i][j] = dp[i-1][j-1] + curr; } else { dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + curr; } } } int res = dp[triangle.size()-1][0]; for (int j = 1; j < triangle.size(); j++) { res = Math.min(res, dp[triangle.size()-1][j]); } return res; } } ``` 下面來分析這個問題的時間複雜度以及空間複雜度，一般來說空間複雜度是就是 DP 表格的大小。 在這道問題中是 `O(n^2)`，而對於時間複雜度來說，就是整個 dp 的遍歷次數，而在這個問題中我們只進行了一次遍歷，也即一個矩陣的遍歷，所以是`O(n^2)`。 而如果想要優化到 `O(n)`，我們需要怎麼做呢？ 實際上這個就涉及到了一種**狀態壓縮**的方法，也即壓縮這個狀態表。 那麼怎麼去壓縮呢？ 這個問題比較簡單，因為`dp[i][j]`僅僅與上一層的狀態有關，所以說與前兩層的是沒有任何關係的，因此我們不必儲存這些無關的狀態。 實際上最簡單的狀態壓縮就是保留好前兩個狀態即可，例如在計算第四行的時候，保留第三行以及第二行的狀態表，然後交替的進行更新就可以啦。 ```java class Solution { public int minimumTotal(List> triangle) { // 只保留最近 2 行 int[][] dp = new int[2][triangle.size()]; dp[0][0] = triangle.get(0).get(0); for (int i = 1; i < triangle.size(); i++) { int row = i % 2; int prevRow = (i-1) % 2; for (int j = 0; j <= i; j++) { if (j == 0) { dp[row][j] = dp[prevRow][j] + triangle.get(i).get(j); } else if (j == i) { dp[row][j] = dp[prevRow][j-1] + triangle.get(i).get(j); } else { dp[row][j] = Math.min(dp[prevRow][j-1], dp[prevRow][j]) + triangle.get(i).get(j); } } } int res = dp[(triangle.size() - 1) % 2][0]; for (int j = 1; j < triangle.size(); j++) { res = Math.min(res, dp[(triangle.size() - 1) % 2][j]); } return res; } } ``` 這個的空間複雜度是 `O(2n)`，能不能壓縮成嚴格意義上的`O(n)`呢？ 那麼再往後是否還能夠進行狀態的壓縮呢？ 答案是可以的，我們可以再想一種方程然後達到最優的空間複雜度的目標。 當我們在計算位置 `[i][j]` 時，`f[j+1]` 到 `f[i]` 已經是第 `i` 行的值，而 `f[0]` 到 `f[j]` 仍然是第 `i-1` 行的值。 此時我們直接通過 `f[j] = min(f[j−1], f[j]) + c[i][j]`來計算，但是這個時候我們需要`j` 是倒著遍歷的，因為這樣才不會影響之前記錄下的狀態。 如果從 1 開始，那麼計算 2 的時候就會用到新的 1 的數值而不是上一層 1 的數值。 程式碼如下： ```python class Solution { public int minimumTotal(List> triangle) { int[] dp = new int[triangle.size()]; dp[0] = triangle.get(0).get(0); for (int i = 1; i < triangle.size(); i++) { dp[i] = dp[i-1] + triangle.get(i).get(i); for (int j = i-1; j > 0; j--) { dp[j] = Math.min(dp[j-1], dp[j]) + triangle.get(i).get(j); } dp[0] += triangle.get(i).get(0); } int res = dp[0]; for (int j = 1; j < triangle.size(); j++) { res = Math.min(res, dp[j]); } return res; } } ``` ### 方法 2 方法 1 有點繞，但如果自下向上來理解，就會變得很簡單，這個方法也叫 `bottom-up`，方法 1 則是 `top-down`。 從結果出發，這個問題是一個**發散三角樹**的問題，從最後一行出發，然後每一行每一行的進行遞推，那麼第一行就是最終的結果了。 舉個最簡單的例子： ``` 1 1 2 ``` 如果從最底下往上出發，實際上找最小值方法的規律很容易找到，那就是在第二行`[1， 2]`裡面選擇一個就可以了，因為他們兩個都要走到根節點。 也就是在下一行的兩個數裡面取個小的就行了，那麼結果就是第一行的數值。 我們先用二維的轉移矩陣來解釋這個問題，用這種方法也不需要考慮方法 1 裡面的邊界條件了： `dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + c[i][j]` 狀態轉換圖如下所示：  ```java class Solution { public int minimumTotal(List> triangle) { int[][] dp = new int[triangle.size()][triangle.size()]; // 建立 DP 空間 for (int i = 0; i < triangle.size(); i++) { dp[triangle.size() - 1][i] = triangle.get(triangle.size() - 1).get(i); } for (int i = triangle.size() - 2; i >= 0; i--) { for (int j = 0; j < triangle.get(i).size(); j++) { dp[i][j] = Math.min(dp[i+1][j], dp[i+1][j+1]) + triangle.get(i).get(j); } } return dp[0][0]; } } ``` 那麼在進行狀態壓縮的時候，我們該怎麼去做呢？ 實際上就是隻用一個狀態表來表示所有的。 因為只是和上一個狀態相關，所以說可以表示成如下的形式： `dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j]`， 我們只用 `j` 來代表當前的狀態，然後最終輸出`dp[0]`即可。 ```java class Solution { public int minimumTotal(List> triangle) { int[] dp = new int[triangle.size()]; // 建立 DP 空間 for (int i = 0; i < triangle.size(); i++) { dp[i] = triangle.get(triangle.size() - 1).get(i); } for (int i = triangle.size() - 2; i >= 0; i--) { for (int j = 0; j <= i; j++) { dp[j] = Math.min(dp[j], dp[j+1]) + triangle.get(i).get(j); } } return dp[0]; } } ``` # 總結 以上就是動態規劃解題方法的粗淺介紹，總的來說，我們需要注意動態規劃的這麼幾件事情。 1. 確定是否需要用動態規劃； 2. 確定動態規劃的四個部分； 3. 寫程式碼。 實際上難點就是`轉移方程`，這個確實需要大量的積累才能夠在面試的時候看穿，甚至有些題沒見過的話就是想不出來的。 但是沒見過就做不出來的題面試一般也不會考，所以大家也不用太擔心，重點還是掌握方法，舉一反三。 接下來我也會歸納總結一些動態規劃的常見題型，和大家一起探索`最優解`。 更多演算法文章，建議收藏這個連結： - [齊姐聊演算法](https://mp.weixin.qq.com/mp/appmsgalbum?action=getalbum&album_id=1337155274347692033&__biz=MzIzNDQ3MzgxMw==#wechat_redirect) --- 我是小齊，後端開發工程師，座標紐約，曾在投行做 Quant，後加入科技公司 FLAG 中的一家。 業餘時間打理公粽號【NYCSDE】，更新略少，乾貨很多，建議加個星標防止錯過。