動態規劃解題入門
動態規劃是一種演算法思想,剛入門的時候可能感覺十分難以掌握,總是會有看了題不知道怎麼做,但是一看答案就恍然大悟的感覺。結合這一段時間的學習,在這裡做一下總結。
解題思路
在解題的過程中,首先可以主動尋找遞推關係,比如對當前陣列進行逐步拉伸,看新的元素和已有結果是否存在某種關係。
對於沒有思路的題目,求解可以分為暴力遞迴(回溯),記憶性搜尋,遞迴優化,時間或空間最終優化四個階段。
在碰到一道可以使用動態規劃的題目的時候,如果還不知道怎麼下手,那麼第一步,一定要去想如何遞迴求解。
所謂遞迴求解,說的簡單點,就是一種窮舉,文藝一點,也可以叫回溯。是的,在學習動態規劃之前,一定要對回溯法有所瞭解。
backtracking(member){
//如果已經不可能再得到結果,直接返回。也叫剪枝,分支限界。
if(is_invalid) return;
//如果得到最終結果,處理顯示。
if(is_solution) print_result();
//遞迴即將進入下一層級,如果有資料在下一層級中需要使用,更新它們。
move_ahead();
//準備要進入遞迴的元素。
candidate[] candidates = get_candidates;
for 上面就是回溯法的基本模板,看清來可能有點模糊,下面的第一道題目的第一個步驟,就將對此作出詳細解釋。
題目1
給一個非負陣列,你一開始處在陣列收尾(index=0),陣列中元素代表你能從當前位置向後跳的**最大**步數,問能否達到陣列末尾。比如:
A = [2,3,1,1,4], return true.
A = [3 遞迴求解
最為直觀的回溯法求解如下:
思路十分直觀,當我們到了每個位置,在此位置上,可以向後跳1到最大步數,在每一跳之後進行遞迴,依次類推窮舉出所有情況,一旦有一種可以到達最終位置,那麼我們就可以得到最終結果。
public class Solution {
public boolean canJumpFromPosition(int position, int[] nums) {
if (position == nums.length - 1) {
return true;
}
int furthestJump = Math.min(position + nums[position], nums.length - 1);
for (int nextPosition = position + 1; nextPosition <= furthestJump; nextPosition++) {
if (canJumpFromPosition(nextPosition, nums)) {
return true;
}
}
return false;
}
public boolean canJump(int[] nums) {
return canJumpFromPosition(0, nums);
}
}首先先進行一下簡單的優化,在每一步判斷下一跳位置的時候,為了儘快的到達最後的位置,我們很明顯應該儘可能多走步數,一旦發現最後無法到達再減少步數。
// 原始程式碼
for (int nextPosition = position + 1; nextPosition <= furthestJump; nextPosition++)
// 新的程式碼
for (int nextPosition = furthestJump; nextPosition > position; nextPosition--)記憶化搜尋(自頂向下動態規劃)
可以看到,上面的遞迴基本就是暴力解法,那麼進一步的優化,就是在遞迴上面應用儲存,已經計算過的分支不再繼續進行計算。
public class Solution {
Index[] memo;
public boolean canJumpFromPosition(int position, int[] nums) {
//儲存已經計算過的分支
if (memo[position] != Index.UNKNOWN) {
return memo[position] == Index.GOOD ? true : false;
}
int furthestJump = Math.min(position + nums[position], nums.length - 1);
for (int nextPosition = position + 1; nextPosition <= furthestJump; nextPosition++) {
if (canJumpFromPosition(nextPosition, nums)) {
memo[position] = Index.GOOD;
return true;
}
}
memo[position] = Index.BAD;
return false;
}
public boolean canJump(int[] nums) {
memo = new Index[nums.length];
for (int i = 0; i < memo.length; i++) {
memo[i] = Index.UNKNOWN;
}
memo[memo.length - 1] = Index.GOOD;
return canJumpFromPosition(0, nums);
}
}去遞迴(自底向上動態規劃)
去遞迴的過程,其實就是人為的分析並指定計算過程的過程。
首先分析遞迴過程中的可變引數,這個可變引數就是迴圈中遍歷的變數。這裡很明顯是當前位置 position。
然後需要分析遞迴的執行順序,這裡可以人為畫遞迴樹。我們可以發現,運算實質是從右向左進行的。一個點能否達到某一個點,取決於它右邊點的運算結果。
enum Index {
GOOD, BAD, UNKNOWN
}
public class Solution {
public boolean canJump(int[] nums) {
Index[] memo = new Index[nums.length];
for (int i = 0; i < memo.length; i++) {
memo[i] = Index.UNKNOWN;
}
memo[memo.length - 1] = Index.GOOD;
for (int i = nums.length - 2; i >= 0; i--) {
int furthestJump = Math.min(i + nums[i], nums.length - 1);
//去當前點的右邊看是否有可達點。
for (int j = i + 1; j <= furthestJump; j++) {
if (memo[j] == Index.GOOD) {
memo[i] = Index.GOOD;
break;
}
}
}
return memo[0] == Index.GOOD;
}
}貪心優化(貪心策略)
上面的時間複雜度為O(mn),m是陣列中最大值,n是陣列個數。在分析上面迴圈的過程中,我們發現找到的第一個點可以到達一個可達點,那麼當前位置就不需要再判斷後面的步數。也就是說,一個點只要找到離他最近的可達點,那麼它就變成了下一輪的可達點。下一輪一旦有一個點可以達到它,那麼該點又成為下一輪新的可達點。
這也就告訴我們,對於每個點,只要找到它右邊第一個可達點即可。
這也就是典型的貪心策略。
我們可以從右向左,在某個可達點左邊找一個最近的點可以達到它,更新該最近點為新的可達點,以此類推,知道最後的一個可達點是起始點。
public class Solution {
public boolean canJump(int[] nums) {
int lastPos = nums.length - 1;
for (int i = nums.length - 1; i >= 0; i--) {
if (i + nums[i] >= lastPos) {
lastPos = i;
}
}
return lastPos == 0;
}
}題目2
給一個非負陣列,從陣列中選取任意個數字求和,要求所選元素均不相鄰,求最大和。
直接尋找遞迴關係
對於比較簡單的dp,也可以尋找遞推關係求解:
這到題的遞推關係在於,對於每一個新的元素,都可以選擇取或者不取,用一個數組dp記錄前面不同長度陣列的最大和,那麼對當前元素dp[i],如果不取則最大和為dp[i-1],如果取則最大值為dp[i-2]+num[i];可以很輕易的根據遞推關係寫出動態規劃:
public class Solution {
public int rob(int[] nums) {
if(nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length+1];
dp[0] = 0;
dp[1] = nums[0];
for(int i = 2;i<nums.length;i++){
dp[i] = Math.max(dp[i-1],nums[i]+dp[i-2]);
}
return dp[nums.length];
}
空間優化
到這裡還不算完,我們看見,對於每個dp[i]的計算,僅和dp[i-1],dp[i-2]有關,這也告訴我們根本不需要一個數組,因為以前用過的值在後面不會再使用。這樣,僅僅使用兩個變數就可以達到效果,空間複雜度也從O(N)降到了O(1)。
public class Solution {
public int rob(int[] nums) {
if(nums == null || nums.length == 0) return 0;
int a =0,b = nums[0];
for(int i=1;i<nums.length;i++){
int temp = b;
b = Math.max(b,a+nums[i]);
a = temp;
}
return b;
}
}題目3
一個二維非負陣列,找出從最左上到最右下的最小距離,只可以向右或者向下移動。
直接尋找遞推關係
這道題基本是二維中最簡單的了,直接看到某一點(i,j)的最短距離怎麼求就可以。用二維陣列記錄到每個點的最短距離dp[i][j],可以直接根據遞推關係 dp[i][j] = min{dp[i-1][j],dp[i][j-1]}就可以求解。
二維空間優化
一維動態規劃可以通過空間優化達到常數級別的空間複雜度,同樣二維動態規劃也可以進一步優化。
首先,根據遞迴關係,我們發現每個位置只和上面i-1和左邊j-1的值有關,於是可以採用陣列滾動的方法。
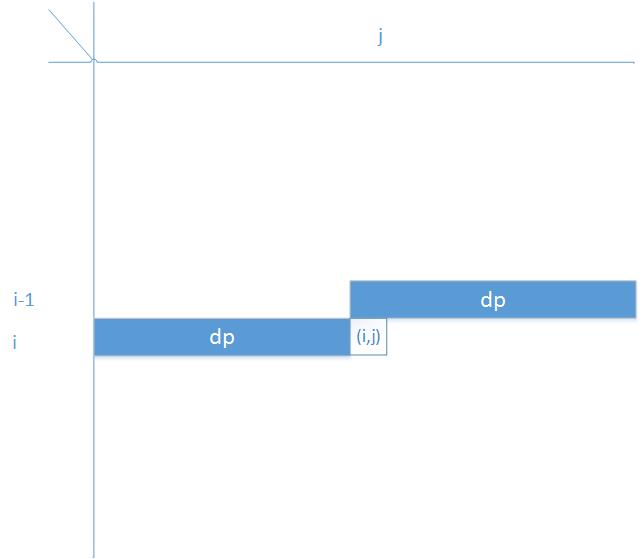
在計算第i行的時候,只儲存第i-1行的最短距離,比如計算(i,j)點,陣列中dp[j]到右邊的元素是二維表中(i-1,j)右邊的元素。而陣列中 dp[j-1]以及其左邊的元素,是 二維表中 (i,j-1)及其左邊的元素。
其實,就是計算將第i行計算過的結果存在陣列前半部分,而後半部分是之前計算上一行儲存的最短距離,用於以後計算使用。相當於通過滾動,覆蓋了不再被需要的值。
如下面的簡圖,其實就是把一個數組分成兩半,左邊儲存dp[i][j-1]所要用的資料,右邊是dp[i-1][j]使用的資料。
優化過的程式碼如下,空間複雜度降到了O(n).
public class Solution {
public int minPathSum(int[][] grid) {
//空間壓縮,陣列滾動方法。
int m = grid.length,n = grid[0].length;
int[] dp = new int[n];
dp[0] = grid[0][0];
for(int i=1;i<n;i++)
dp[i] =dp[i-1] + grid[0][i];
for(int i=1;i<m;i++)
for(int j=0;j<n;j++)
dp[j] = (j>0?Math.min(dp[j - 1],dp[j]):dp[j]) + grid[i][j];
return dp[n-1];
}
}題目4、5:
這兩道題目是一維的動態規劃,對於一維的動態規劃很難從基本的暴力解法逐步推導過去,更多的是尋找遞推關係,類似於鋼條切割問題。個人還是比較頭疼的。
第一個題目:
地址:https://leetcode.com/problems/maximum-subarray/
題目是在一個數組中,尋找連續的數,獲得最大和。
比如:[-2,1,-3,4,-1,2,1,-5,4]陣列,最大和是子陣列[4,-1,2,1]為6。
一維動態規劃,尋找遞推關係。為了表明是dp問題,設定一個數組,dp[i]表示包含nums[i]的子陣列的最大和。從左到右遍歷陣列,每新添一個數時,計算dp[i],可以知道新添的數要麼和前面最大和子陣列累加,得到dp[i]+nums[i],要麼自己作為一個新的子陣列的唯一元素,和是nums[i],則有遞推關係 dp[i] = max(nums[i],dp[i-1] * nums[i])。
注意,dp[i]是包含第i個元素的區域性最優解,全域性最優解每次獲得區域性最優解比較一下就行。
程式碼如下:
public class Solution {
//空間可以被優化
public int maxSubArray(int[] nums) {
if(nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length];
int r = nums[0];
dp[0] = nums[0];
for(int i=1;i<nums.length;i++){
int n = nums[i];
dp[i] = Math.max(n,dp[i-1]+n);
r = Math.max(dp[i],r);
}
return r;
}
}第二個題目類似,只不過是乘法最大值。乘法就是要跟蹤一下區域性的最大值和最小值即可,因為乘法最小值乘以負數也可能出現最大值。程式碼如下:
public class Solution {
public int maxProduct(int[] nums) {
if(nums == null || nums.length == 0) return 0;
int[] max = new int[nums.length];
int[] min = new int[nums.length];
int r = nums[0];
max[0] = r;
min[0] = r;
for (int i = 1;i<nums.length;i++) {
int n = nums[i];
int a = max[i - 1] * n;
int b = min[i - 1] * n;
max[i] = Math.max(n, Math.max(a,b));
min[i] = Math.min(n, Math.min(a, b));
r = Math.max(max[i], r);
}
return r;
}
}很明顯,兩個題目都可以優化成O(1)空間,這裡為了表示明顯不進行優化,讀者可以自己嘗試一下。