主題模型（topic model）是以非監督學習的方式對文集的隱含語義結構（latent semantic structure）進行聚類（clustering）的統計模型。

　　主題模型主要被用於自然語言處理（Natural language processing）中的語義分析（semantic analysis）和文字挖掘（text mining）問題，例如按主題對文字進行收集、分類和降維；也被用於生物資訊學（bioinfomatics）研究 [2] 。隱含狄利克雷分佈（Latent Dirichlet Allocation, LDA）是常見的主題模型。

1. LDA貝葉斯模型

　　LDA是基於貝葉斯模型的，涉及到貝葉斯模型離不開“先驗分佈”，“資料（似然）”和"後驗分佈"三塊。在樸素貝葉斯演算法原理小結中我們也已經講到了這套貝葉斯理論。在貝葉斯學派這裡：

先驗分佈 + 資料（似然）= 後驗分佈

　　這點其實很好理解，因為這符合我們人的思維方式，比如你對好人和壞人的認知，先驗分佈為：100個好人和100個的壞人，即你認為好人壞人各佔一半，現在你被2個好人（資料）幫助了和1個壞人騙了，於是你得到了新的後驗分佈為：102個好人和101個的壞人。現在你的後驗分佈裡面認為好人比壞人多了。這個後驗分佈接著又變成你的新的先驗分佈，當你被1個好人（資料）幫助了和3個壞人（資料）騙了後，你又更新了你的後驗分佈為：103個好人和104個的壞人。依次繼續更新下去。

2. 二項分佈與Beta分佈

　　對於上一節的貝葉斯模型和認知過程，假如用數學和概率的方式該如何表達呢？

　　對於我們的資料（似然），這個好辦，用一個二項分佈就可以搞定，即對於二項分佈：

$Binom(k|n,p)=\binom{n}{k}p^{k}(1-p)^{n-k}$

　　其中$p$我們可以理解為好人的概率，$k$為好人的個數，$n$為好人壞人的總數。

　　雖然資料(似然)很好理解，但是對於先驗分佈，我們就要費一番腦筋了，為什麼呢？因為我們希望這個先驗分佈和資料（似然）對應的二項分佈集合後，得到的後驗分佈在後面還可以作為先驗分佈！就像上面例子裡的“102個好人和101個的壞人”，它是前面一次貝葉斯推薦的後驗分佈，又是後一次貝葉斯推薦的先驗分佈。也即是說，我們希望先驗分佈和後驗分佈的形式應該是一樣的，這樣的分佈我們一般叫共軛分佈。在我們的例子裡，我們希望找到和二項分佈共軛的分佈。

　　和二項分佈共軛的分佈其實就是Beta分佈。Beta分佈的表示式為：

$Beta(p|\alpha ,\beta )= \frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha \Gamma (\beta ))}p^{\alpha -1}(1-p)^{\beta -1}$

　　其中$\Gamma$是Gamma函式，滿足$\Gamma (x)=(x-1)!$　　

　　仔細觀察Beta分佈和二項分佈，可以發現兩者的密度函式很相似，區別僅僅在前面的歸一化的階乘項。那麼它如何做到先驗分佈和後驗分佈的形式一樣呢？後驗分佈$P(p|n,k,\alpha ,\beta )$推導如下：

$P(p|n,k,\alpha ,\beta )\propto P(k|n,p)P(p|\alpha ,\beta )=P(k|n,p)P(p|\alpha ,\beta )=Binom(k|n,p)Beta(p|\alpha ,\beta )=\binom{n}{k}p^{k}(1-p)^{n-k}\times \frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}p^{\alpha -1}(1-p)^{\beta -1}\propto p^{k+\alpha -1}(1-p)^{n-k+\beta -1}$

　　將上面最後的式子歸一化以後，得到我們的後驗概率為：

$P(p|n,k,\alpha ,\beta )=\frac{\Gamma (\alpha +\beta +n)}{\Gamma (\alpha+k) \Gamma (\beta+n-k)}p^{k+\alpha -1}(1-p)^{n-k+\beta -1}$

　　可見我們的後驗分佈的確是Beta分佈，而且我們發現：

$Beta(p|\alpha ,\beta )+BinomCount(k,n-k)=Beta(p|\alpha+k ,\beta+n-k )$

　　這個式子完全符合我們在上一節好人壞人例子裡的情況，我們的認知會把資料裡的好人壞人數分別加到我們的先驗分佈上，得到後驗分佈。　

　　我們在來看看Beta分佈$Beta(p|\alpha ,\beta )$的期望：

$E(Beta(p|\alpha ,\beta ))=\int_{0}^{1}tBeta(p|\alpha ,\beta )dt=\int_{0}^{1}\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}t^{\alpha -1}(1-t)^{\beta -1}dt=\int_{0}^{1}\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}t^{\alpha}(1-t)^{\beta -1}dt$

　　由於上式最右邊的乘積對應Beta分佈$Beta(p|\alpha+1 ,\beta )$，因此有：

$\int_{0}^{1}\frac{\Gamma (\alpha +\beta +1)}{\Gamma (\alpha+1 )\Gamma (\beta )}p^{\alpha}(1-p)^{\beta -1}dp=1$

　　這樣我們的期望可以表達為：

$E(Beta(p|\alpha ,\beta ))=\frac{\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}\frac{\Gamma (\alpha +1)\Gamma (\beta )}{\Gamma (\alpha+\beta +1 )}=\frac{\alpha }{\alpha +\beta }$

　　這個結果也很符合我們的思維方式。

3. 多項分佈與Dirichlet 分佈

　　現在我們回到上面好人壞人的問題，假如我們發現有第三類人，不好不壞的人，這時候我們如何用貝葉斯來表達這個模型分佈呢？之前我們是二維分佈，現在是三維分佈。由於二維我們使用了Beta分佈和二項分佈來表達這個模型，則在三維時，以此類推，我們可以用三維的Beta分佈來表達先驗後驗分佈，三項的多項分佈來表達資料（似然）。

　　三項的多項分佈好表達，我們假設資料中的第一類有$m_{1}$個好人，第二類有$m_{2}$個壞人，第三類為$m_{3}=n-m_{1}-m_{2}$個不好不壞的人，對應的概率分別為$p_{1}$,$m_{2}$,$m_{3}=n-m_{1}-m_{2}$，則對應的多項分佈為：

$multi(m_{1},m_{2},m_{3}|n,p_{1},p_{2},p_{3})=\frac{n!}{m_{1}!m_{2}!m_{3}!}p_{1}^{m_{1}}p_{2}^{m_{2}}p_{3}^{m_{3}}$

　　那三維的Beta分佈呢？超過二維的Beta分佈我們一般稱之為狄利克雷(以下稱為Dirichlet )分佈。也可以說Beta分佈是Dirichlet 分佈在二維時的特殊形式。從二維的Beta分佈表示式，我們很容易寫出三維的Dirichlet分佈如下：

$Dirichlet(p_{1},p_{2},p_{3}|\alpha _{1},\alpha _{2},\alpha _{3})=\frac{\Gamma (\alpha _{1}+\alpha _{2}+\alpha _{3})}{\Gamma(\alpha _{1} )\Gamma (\alpha _{2})\Gamma (\alpha _{3})}p_{1}^{\alpha _{1}-1}p_{2}^{\alpha _{2}-1}p_{3}^{\alpha _{3}-1}$

　　同樣的方法，我們可以寫出4維，5維，。。。以及更高維的Dirichlet 分佈的概率密度函式。為了簡化表示式，我們用向量來表示概率和計數,這樣多項分佈可以表示為：$Dirichlet(\overrightarrow{p}|\overrightarrow{\alpha})$，而多項分佈可以表示為：$multi(\overrightarrow{m}|n,\overrightarrow{p})$

　　一般意義上的K維Dirichlet 分佈表示式為：

$Dirichlet(\overrightarrow{p}|\overrightarrow{\alpha})=\frac{\Gamma (\sum_{k=1}^{K}\alpha _{k})}{\prod_{k=1}^{K}\Gamma (\alpha _{k})}\prod_{k=1}^{K}p_{k}^{\alpha _{k}-1}$

　　而多項分佈和Dirichlet 分佈也滿足共軛關係，這樣我們可以得到和上一節類似的結論：

$Dirichlet(\overrightarrow{p}|\overrightarrow{\alpha})+MultiCount(\overrightarrow{m})=Dirichlet(\overrightarrow{p}|\overrightarrow{\alpha}+\overrightarrow{m})$

　　對於Dirichlet 分佈的期望，也有和Beta分佈類似的性質：

$E(Dirichlet(\overrightarrow{p}|\overrightarrow{\alpha}))=(\frac{\alpha _{1}}{\sum_{k=1}^{K}},\frac{\alpha _{2}}{\sum_{k=1}^{K}},\cdots ,\frac{\alpha _{K}}{\sum_{k=1}^{K}})$

4. LDA主題模型

　　前面做了這麼多的鋪墊，我們終於可以開始LDA主題模型了。

　　我們的問題是這樣的，我們有M篇文件，對應第d個文件中有有N_d個詞。即輸入為如下圖：

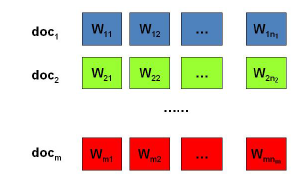
　　　　我們的目標是找到每一篇文件的主題分佈和每一個主題中詞的分佈。在LDA模型中，我們需要先假定一個主題數目K，樣所有的分佈就都基於K個主題展開。那麼具體LDA模型是怎麼樣的呢？具體如下圖：

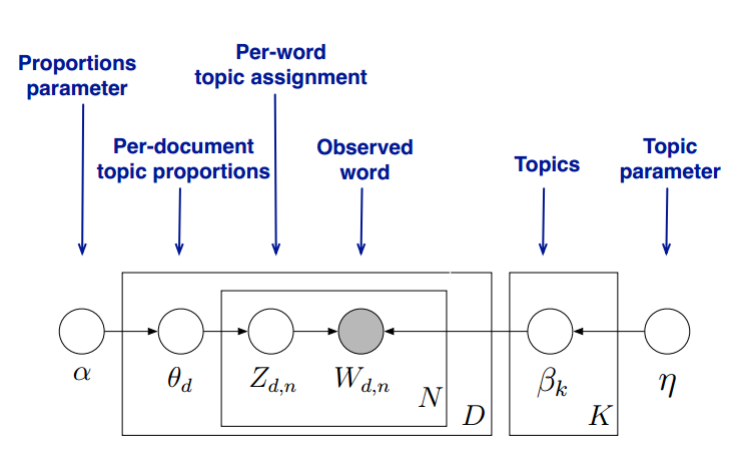　　LDA假設文件主題的先驗分佈是Dirichlet分佈，即對於任一文件d，其主題分佈$\theta _{d}$為：

$\theta _{d}=Dirichlet(\overline{\alpha })$

　　其中，$\alpha $為分佈的超引數，是一個K維向量。

　　LDA假設主題中詞的先驗分佈是Dirichlet分佈，即對於任一主題k，其詞分佈$\beta _{k}$為：

$\beta _{k}=Dirichlet(\overline{\eta })$

　　其中，$\eta$為分佈的超引數，是一個V維向量。V代表詞彙表裡所有詞的個數。

　　對於資料中任一一篇文件d中的第n個詞，我們可以從主題分佈$\theta _{d}$中得到它的主題編號$z_{dn}$的分佈為：

$z_{dn}=multi(\theta _{d})$

　　而對於該主題編號，得到我們看到的詞$\omega z_{dn}$的概率分佈為：

$\omega z_{dn}=multi(\beta _{zdn})$

　　理解LDA主題模型的主要任務就是理解上面的這個模型。這個模型裡，我們有M個文件主題的Dirichlet分佈，而對應的資料有M個主題編號的多項分佈，這樣($\alpha \rightarrow \theta _{d}\rightarrow \overrightarrow{{z}_{d}}$)就組成了Dirichlet-multi共軛，可以使用前面提到的貝葉斯推斷的方法得到基於Dirichlet分佈的文件主題後驗分佈。

　　如果在第d個文件中，第k個主題的詞的個數為：$n_{d}^{k}$，則對應的多項分佈的計數可以表示為：

$\overrightarrow{n}_{d}=(n_{d}^{1},n_{d}^{2},\cdots ,n_{d}^{K})$

　　利用Dirichlet-multi共軛，得到$\theta _{d}$的後驗分佈為：

$Dirichlet(\theta _{d}|\overrightarrow{\alpha}+\overrightarrow{n}_{d})$

　　同樣的道理，對於主題與詞的分佈，我們有