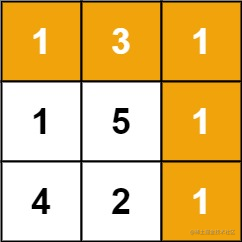
想必很多人還不知道動態規劃是可以狀態壓縮的吧，通俗的講就是把維數變小，一般就是把二維陣列降為一維。維數變小意味著空間變小，速度還不變，不用空間換時間，這就是狀態壓縮的強大之處。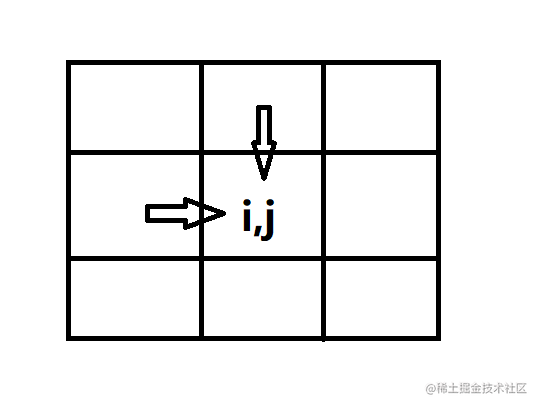 以leetcode64題最小路徑和為例，帶大家一步一步見識一下狀態壓縮這個小技巧 題意：給定一個包含非負整數的 m x n 網格 grid ，請找出一條從左上角到右下角的路徑，使得路徑上的數字總和為最小 說明：每次只能向下或者向右移動一步 示例1  輸入：grid = [[1,3,1],[1,5,1],[4,2,1]] 輸出：7 解釋：因為路徑 1→3→1→1→1 的總和最小 函式名： ``` public int minPathSum(int[][] grid) ``` 題目的最基本的狀態轉移方程是 dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]; 意思是如果我們在i, j 這個位置的話從可以從兩個方向推出dp[i][j]的值，題目說明了每次只能向下或者向右移動一步，如下圖  完整程式碼如下 ``` class Solution { public int minPathSum(int[][] grid) { if (grid.length == 0) return 0; int n = grid.length; int m = grid[0].length; int[][] dp = new int[n][m]; dp[0][0] = grid[0][0]; //初始化 //從（0，0）一直向下走 for (int i = 1; i < n; i++) dp[i][0] = dp[i - 1][0] + grid[i][0]; //從（0，0）一直向右走 for (int j = 1; j < m; j++) dp[0][j] = dp[0][j - 1] + grid[0][j]; //狀態轉移 for (int i = 1; i < n; i++) for (int j = 1; j < m; j++) dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]; return dp[n - 1][m - 1]; } } ``` 上面的測試用例執行後的dp陣列如下  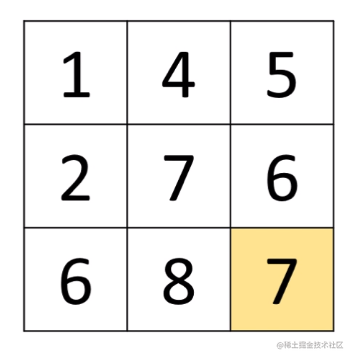上面的程式碼很直觀吧 下面的程式碼是為了推出狀態壓縮而寫的，原理和上面一樣，只是上面的dp[0][0]換成下面的dp[1][1] 我這樣子寫不是說要這樣子做，只是為了方便大家理解狀態壓縮而已，基本思路完全沒有變 先貼出dp陣列結果如下  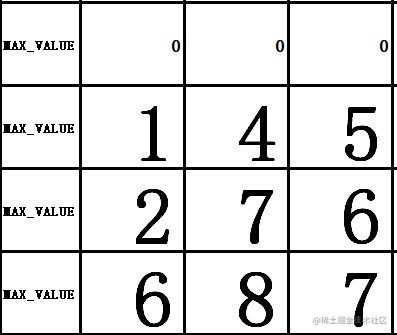程式碼如下 ``` class Solution { public int minPathSum(int[][] grid) { if (grid.length == 0) return 0; int n = grid.length; int m = grid[0].length; int[][] dp = new int[n + 1][m + 1]; //初始化 for (int i = 0; i <= n; i++) dp[i][0] = Integer.MAX_VALUE; dp[1][1] = grid[0][0]; //初始狀態 //從（1，1）一直往右走 for (int j = 2; j <= m; j++) dp[1][j] = dp[1][j - 1] + grid[0][j - 1]; //狀態轉移 for (int i = 2; i <= n; i++) for (int j = 1; j <= m; j++) dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1]; return dp[n][m]; } } ``` 接下來開始進行狀態壓縮 把二維降為一維結果如下,採用的是**直接**投影的方法  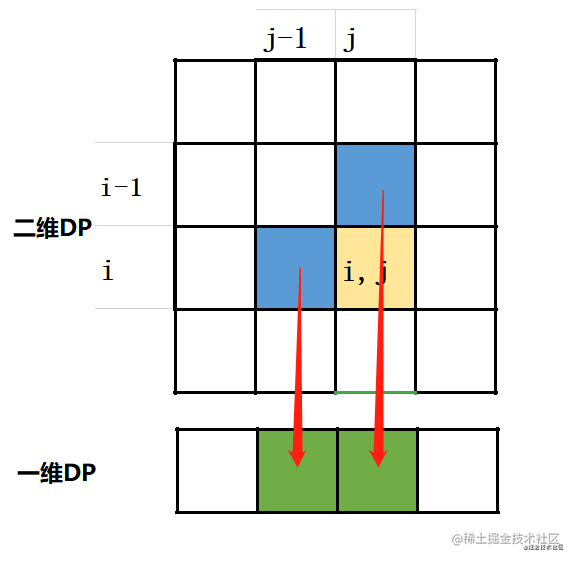投影也就是**直接把dp[i][j]中i所在的那一維去掉** 程式碼的轉變過程如下 由 ``` dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1] ``` 變成 ``` dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i - 1][j - 1] ``` 解釋一下上面為什麼這樣子就完成了 想要求出dp[i][j]需要先求出dp[i - 1][j]和dp[i][j - 1] 我們發現二維的dp[i - 1][j]對映成了一維的dp[j],dp[i][j - 1]對映成了dp[j - 1] 所需要的資訊都能直接用一維來表示 哪怕dp[j]被覆蓋了也沒事，原因看下圖  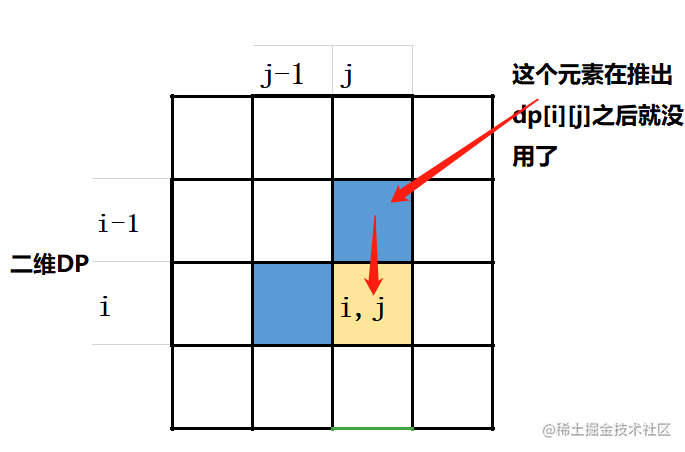所以 ``` dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i - 1][j - 1] ``` 完整程式碼如下： ``` class Solution { public int minPathSum(int[][] grid) { if (grid.length == 0) return 0; int n = grid.length; int m = grid[0].length; int[] dp = new int[m + 1]; //初始化 dp[0] = Integer.MAX_VALUE; dp[1] = grid[0][0]; //從（1，1）一直向右走 真的只是把上面的程式碼中dp[i][j]的i那一維去掉 for (int j = 2; j <= m; j++) dp[j] = dp[j - 1] + grid[0][j - 1]; //這裡也是直接去掉i中的那一維 for (int i = 2; i <= n; i++) for (int j = 1; j <= m; j++) dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i - 1][j - 1]; return dp[m]; } } ``` 這題到這裡也就結束了 這題的狀態壓縮之所以簡單是因為沒有多個元素對映到同一個位置 如果如下圖所示的話  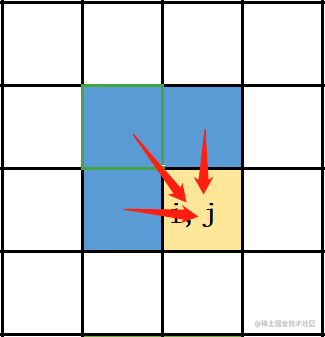一旦對映就會有兩個狀態對映到同一個位置，這裡提示一下，此時也很簡單，只需要**定義一個變數**，來**儲存**那兩個對映到同一個位置的**兩個變數中的其中一個變數**就行了 後面我有空也會寫一下兩個狀態對映到同一位置的這種情況 這裡只是大概幫助你們入一下門。以後你看到有兩個狀態對映到同一位置的狀態壓縮的程式碼時，也能很輕鬆的讀懂 這或許也是為什麼面試官那麼看重計算機基礎，不就是因為計算機基礎是一切的基石，計算機基礎穩了，上手其他那不是手到擒來 圖片目前做的不是很美觀，以後會慢慢優化。 如果覺得有收穫，不妨花個幾秒鐘點個贊，歡迎關注我的公眾號**玩程式設計地碼農**，目前會不斷寫與java、資料結構與演算法和計算機基礎相關的知識等。 ![](https://p9-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/186661b7be4e4a1fa7f5e23f253b2707~tplv-k3u1fbpfcp-watermar