所以我們有了我們的假設函數，我們有一種方法來測量它與數據的吻合程度。現在我們需要估計假設函數中的參數。這就是梯度下降的來源。
想象我們圖基於其領域θ0和θ1我們假設函數（實際上我們是圖形的成本函數作為參數估計的函數）。我們不是繪制x和y本身，而是我們假設函數的參數範圍和選擇一組特定參數所產生的代價
我們把θ0在X軸和Y軸θ1，與成本函數在垂直的Z軸。我們的圖上的點將是使用我們的假設和特定θ參數的代價函數的結果。下圖描述了這樣的設置。

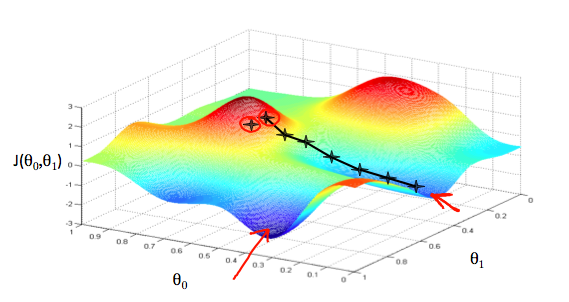
當我們的成本函數位於圖的最底部，即當它的值是最小值時，我們就知道我們已經成功了。紅色箭頭顯示圖中的最小點。

我們這樣做的方法是取我們的成本函數的導數（函數的切線）。切線的斜率是這個點上的導數，它將給我們一個方向。我們把成本函數降到最陡下降的方向。每一步的大小由參數α決定，稱為學習率。

例如，上圖中每個“星”之間的距離代表由我們的參數α決定的步驟。較小的α會導致較小的步長和較大的α結果。這一步是采取的方向是由J的偏導數確定（θ0，θ1）。取決於圖表上的起點，可能會出現不同的點。上面的圖片給我們展示了兩個不同的起點，終點在兩個不同的地

梯度下降算法是：

重復直至收斂：

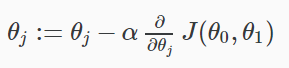
哪裏
J = 0,1代表特征指數。
在每一次叠代，同時應更新參數θθ1，2，…，nθ更新特定的參數來計算一個j^(th)叠代之前，將產生一個錯誤的執行

梯度下降