題目描述

Kiana最近沈迷於一款神奇的遊戲無法自拔。

簡單來說，這款遊戲是在一個平面上進行的。

有一架彈弓位於(0,0)處，每次Kiana可以用它向第一象限發射一只紅色的小鳥，小鳥們的飛行軌跡均為形如的曲線，其中a,b是Kiana指定的參數，且必須滿足a<0。

當小鳥落回地面(即x軸）時，它就會瞬間消失。

在遊戲的某個關卡裏，平面的第一象限中有n只綠色的小豬，其中第i只小豬所在的坐標為(xi,yi)。

如果某只小鳥的飛行軌跡經過了(xi,yi),那麽第i只小豬就會被消滅掉，同時小鳥將會沿著原先的軌跡繼續飛行；

如果一只小鳥的飛行軌跡沒有經過(xi,yi)，那麽這只小鳥飛行的全過程就不會對第i只小豬產生任何影響。

例如，若兩只小豬分別位於(1,3)和(3,3)，Kiana可以選擇發射一只飛行軌跡為的小鳥，這樣兩只小豬就會被這只小鳥一起消滅。

而這個遊戲的目的，就是通過發射小鳥消滅所有的小豬。

這款神奇遊戲的每個關卡對Kiana來說都很難，所以Kiana還輸入了一些神秘的指令，使得自己能更輕松地完成這個遊戲。這些指令將在【輸入格式】中詳述。

假設這款遊戲一共有T個關卡，現在Kiana想知道，對於每一個關卡，至少需要發射多少只小鳥才能消滅所有的小豬。由於她不會算，所以希望由你告訴她。

輸入輸出格式

輸入格式：

第一行包含一個正整數T，表示遊戲的關卡總數。

下面依次輸入這T個關卡的信息。每個關卡第一行包含兩個非負整數n,m，分別表示該關卡中的小豬數量和Kiana輸入的神秘指令類型。接下來的n行中，第i行包含兩個正實數(xi,yi)，表示第i只小豬坐標為(xi,yi)。數據保證同一個關卡中不存在兩只坐標完全相同的小豬。

如果m=0，表示Kiana輸入了一個沒有任何作用的指令。

如果m=1，則這個關卡將會滿足：至多用只小鳥即可消滅所有小豬。

如果m=2,則這個關卡將會滿足：一定存在一種最優解，其中有一只小鳥消滅了至少只小豬。

保證1<=n<=18，0<=m<=2，0<xi,yi<10，輸入中的實數均保留到小數點後兩位。

上文中，符號和分別表示對c向上取整和向下取整

輸出格式：

對每個關卡依次輸出一行答案。

輸出的每一行包含一個正整數，表示相應的關卡中，消滅所有小豬最少需要的小鳥數量

輸入輸出樣例

2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00

1
1

3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00

2
2
3

1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99

6

說明

【樣例解釋1】

這組數據中一共有兩個關卡。

第一個關卡與【問題描述】中的情形相同，2只小豬分別位於（1.00,3.00)和 (3.00,3.00)，只需發射一只飛行軌跡為y = -x^2 + 4x的小鳥即可消滅它們。

第二個關卡中有5只小豬，但經過觀察我們可以發現它們的坐標都在拋物線 y = -x^2 + 6x上，故Kiana只需要發射一只小鳥即可消滅所有小豬。

【數據範圍】

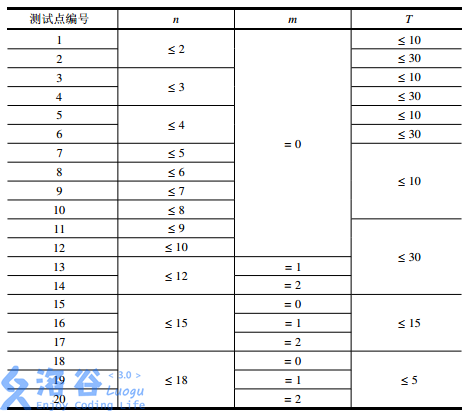
分析：說實話，比較簡單的一道狀壓dp題，可以用一個狀態i表示我們該射哪些鳥，dp[i]為在狀態i下需要的拋物線的數量，那麽可以很容易得到dp[i | 拋物線j射到的豬] = min(dp[i | 拋物線j射到的豬],dp[i] + 1),那麽唯一的難點就是求出拋物線j射到哪些豬了，因為只需要2個點就可以確定一條拋物線，先枚舉兩頭豬，確定一條拋物線，將a > 0的去掉，然後在枚舉看哪些豬在這條拋物線上就可以了，不過需要註意的三個特殊情況：1.精度問題

2.拋物線可能只能打到一頭豬 3.拋物線上兩個點橫坐標不能相同.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <string>

using namespace std;

int T, n, m,zhuangtai[20][20],dp[1 << 20];

struct node
{
    double x, y;
}e[20];

bool jingdu(double a, double b)
{
    return fabs(a - b) < 1e-6;
}

int main()
{
    scanf("%d", &T);
    while (T--)
    {
        memset(zhuangtai, 0, sizeof(zhuangtai));
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
            scanf("%lf%lf", &e[i].x, &e[i].y);
        for (int i = 1; i <= n; i++)
            for (int j = i + 1; j <= n; j++)
                if (i != j)
                {
                    if (jingdu(e[i].x, e[j].x))
                        continue;
                    double a = (e[j].y / e[j].x - e[i].y / e[i].x) / (e[j].x - e[i].x);
                    double b = e[i].y / e[i].x - a * e[i].x;
                    if (a >= 0.0)
                        continue;
                    for (int k = 1; k <= n; k++)
                        if (jingdu(a * e[k].x * e[k].x + b * e[k].x, e[k].y))
                            zhuangtai[i][j] |= (1 << (k - 1));
                }
        for (int i = 1; i < (1 << n); i++)
            dp[i] = 2000000000;
        dp[0] = 0;
        for (int i = 0; i < (1 << n); i++)
            for (int j = 1; j <= n; j++)
                if (!(i & (1 << (j - 1))))
                    for (int k = j; k <= n; k++)
                    {
                        if (k == j)
                            dp[i | (1 << (j - 1))] = min(dp[i | (1 << (j - 1))], dp[i] + 1);
                        if (jingdu(e[j].x, e[k].x))
                            continue;
                        dp[i | zhuangtai[j][k]] = min(dp[i | zhuangtai[j][k]], dp[i] + 1);
                    }
        printf("%d\n", dp[(1 << n) - 1]);
    }

    return 0;
}

noip2016 憤怒的小鳥