Description

Kiana最近沈迷於一款神奇的遊戲無法自拔。

簡單來說，這款遊戲是在一個平面上進行的。

有一架彈弓位於(0,0)處，每次Kiana可以用它向第一象限發射一只紅色的小鳥，小鳥們的飛行軌跡均為形如 $y=ax^2+bx$ 的曲線，其中a,b是Kiana指定的參數，且必須滿足a<0。

當小鳥落回地面(即x軸）時，它就會瞬間消失。

在遊戲的某個關卡裏，平面的第一象限中有n只綠色的小豬，其中第i只小豬所在的坐標為(xi,yi)。

如果某只小鳥的飛行軌跡經過了(xi,yi),那麽第i只小豬就會被消滅掉，同時小鳥將會沿著原先的軌跡繼續飛行；

如果一只小鳥的飛行軌跡沒有經過(xi,yi)，那麽這只小鳥飛行的全過程就不會對第i只小豬產生任何影響。

例如，若兩只小豬分別位於(1,3)和(3,3)，Kiana可以選擇發射一只飛行軌跡為 $y=-x^2+4x$ 的小鳥，這樣兩只小豬就會被這只小鳥一起消滅。

而這個遊戲的目的，就是通過發射小鳥消滅所有的小豬。

這款神奇遊戲的每個關卡對Kiana來說都很難，所以Kiana還輸入了一些神秘的指令，使得自己能更輕松地完成這個遊戲。這些指令將在【輸入格式】中詳述。

假設這款遊戲一共有T個關卡，現在Kiana想知道，對於每一個關卡，至少需要發射多少只小鳥才能消滅所有的小豬。由於她不會算，所以希望由你告訴她。

Input

第一行包含一個正整數T，表示遊戲的關卡總數。

下面依次輸入這T個關卡的信息。每個關卡第一行包含兩個非負整數n,m，分別表示該關卡中的小豬數量和Kiana輸入的神秘指令類型。接下來的n行中，第i行包含兩個正實數(xi,yi)，表示第i只小豬坐標為(xi,yi)。數據保證同一個關卡中不存在兩只坐標完全相同的小豬。

保證1<=n<=18，0<=m<=2，0<xi,yi<10，輸入中的實數均保留到小數點後兩位。

Output

對每個關卡依次輸出一行答案。

輸出的每一行包含一個正整數，表示相應的關卡中，消滅所有小豬最少需要的小鳥數量

Range

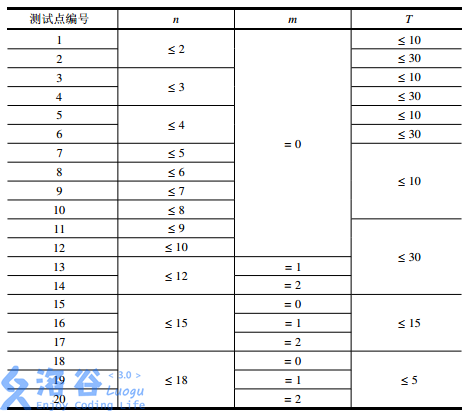
Solution

n≤18，第一反應是爆搜。

碼碼碼，發現只能得 55 分，剩下全 T。

咦，能剪枝！ 剪剪剪，結果兩個點死活過不去。

什麽並查集最優性剪枝各種優化都用上了，剛了一天死活過不去那兩個點。

T 掉的代碼還是放上來吧

// By YoungNeal
#include<cmath>
#include<cstdio>
#include
 
<cstring>
#include<iostream>
#define eps 1e-8
#define r register

int T;
int n,m;
int minn;
double a,b;
bool vis[25];
double zbx[25],zby[25];

int calc(int x){
    double lef=a*zbx[x]*zbx[x]+b*zbx[x];
    double rig=zby[x];
    if(std::fabs(rig-lef)<=eps) return 1;
    return 0;
}

void dfs(int now,int used){
    printf("now=%d,used=%d\n",now,used);
    if(used>=minn) return;
    if(now>n){
        minn=std::min(minn,used);
        return;
    }
    if(vis[now]){
        dfs(now+1,used);
        return;
    }
    vis[now]=1;
    dfs(now+1,used+1);
    printf("back,now=%d\n",now);
    for(r int i=now+1;i<=n;i++){
        printf("i=%d\n",i);
        if(vis[i]) continue;
        double c,d,e,f,g,h;
        c=zbx[now]*zbx[now];
        d=zbx[now]; e=zby[now];
        f=zbx[i]*zbx[i];
        g=zbx[i]; h=zby[i];
        a=(e*g/d-h)/(c*g/d-f);
        b=(h-a*f)/g;
        if(a>=0) continue;
        vis[i]=1;
        int fz[20],cnt=0;
        for(r int j=1;j<=n;j++){
            if(!vis[j]&&calc(j)) fz[++cnt]=j,vis[j]=1;
        }
        dfs(now+1,used+1);
        vis[i]=0;
        for(r int j=1;j<=cnt;j++) vis[fz[j]]=0;
    }
    vis[now]=0;
    printf("return\n");
} 

signed main(){
    scanf("%d",&T);
    while(T--){
        minn=20;
        memset(vis,0,sizeof vis);
        scanf("%d%d",&n,&m);
        for(r int i=1;i<=n;i++) scanf("%lf%lf",&zbx[i],&zby[i]);
        dfs(1,0);
        printf("%d\n",minn);
    }
    return 0;
}

好吧我們考慮狀壓

觀察到，能夠用上的拋物線就那麽幾條，所以不妨都將它們預處理出來。

定義 mp[i][j] 表示必定經過 i，j 兩點的拋物線還能夠經過哪些點。用 01 串來存，第 k 位為 1 表示能經過，否則為不能經過。

定義 dp[i] 表示一個二進制數為 i 時，至少要發射幾只小鳥。

所以轉移方程就很明顯了，dp[i|mp[j][p]]=min{dp[i]+1}

Code

// By YoungNeal
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#define eps 1e-8

int T;
int n,m;
int maxn;
double a,b;
int dp[1<<19];
int mp[20][20]; // mp[i][j]->打i和j能幹掉多少 1 refers to yes 
double x[20],y[20];

bool ok(int i){
    double l=x[i]*x[i]*a+x[i]*b;
    double r=y[i];
    return fabs(r-l)<eps;
}

signed main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m); maxn=1<<n; maxn--;
        memset(dp,0x3f,sizeof dp); dp[0]=0;
        memset(mp,0,sizeof mp);
        for(int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]);
        for(int i=1;i<=n;i++){
            for(int j=i+1;j<=n;j++){
                double c,d,e,f,g,h;
                c=x[i]*x[i]; 
                d=x[i];e=y[i];
                f=x[j]*x[j];
                g=x[j]; h=y[j];
                a=(e*g/d-h)/(c*g/d-f);
                b=(h-a*f)/g;
                if(a>=0) continue;
                for(int k=1;k<=n;k++){
                    if(ok(k)) mp[i][j]|=1<<k-1;
                }
            }
        }
        for(int i=0;i<=maxn;i++){
            for(int j=1;j<=n;j++){
                if(i&(1<<j-1)) continue;
                for(int p=j+1;p<=n;p++)
                    dp[i|mp[j][p]]=std::min(dp[i|mp[j][p]],dp[i]+1);
                dp[i|(1<<j-1)]=std::min(dp[i|(1<<j-1)],dp[i]+1);
            }
        }
        printf("%d\n",dp[maxn]);
    }
    return 0;
}

[Noip2016] 憤怒的小鳥