高階線性微分方程-常微分方程
阿新 • • 發佈:2017-09-01
ans family 次數 com 定義 mage text -a 一個 這裏討論常微分方程。常微分方程的階數就是函數求導的最高次數。這裏以二階線性微分方程為例。
形如方程5的稱為二階線性微分方程。
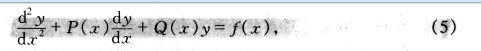
 線性的概念定義為:
線性的概念定義為:

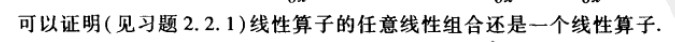 下面討論 二階線性微分方程,這些性質也可以推廣到n階線性方程:
下面討論 二階線性微分方程,這些性質也可以推廣到n階線性方程:
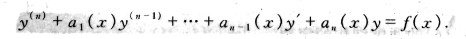 1. 線性微分方程的解的結構
1. 線性微分方程的解的結構
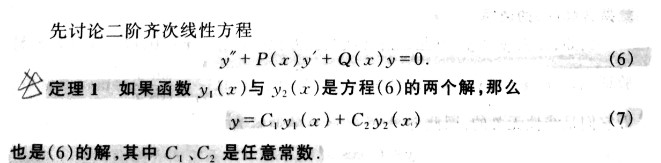 目前,式(7)不是(6)的通解。如何保證通解呢,首先引入函數組線性無關的概念:
目前,式(7)不是(6)的通解。如何保證通解呢,首先引入函數組線性無關的概念:

 下面討論二階非齊次線性方程,非齊次方程的解是齊次方程的通解加上非齊次方程的一個特解構成的。
下面討論二階非齊次線性方程,非齊次方程的解是齊次方程的通解加上非齊次方程的一個特解構成的。
 這一定理稱為線性微分方程的解的疊加原理。
這一定理稱為線性微分方程的解的疊加原理。
以上研究的是高階線性微分方程的解的結構,下面介紹解法,首先討論二階常系數齊次線性微分方程的解法 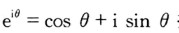 )及疊加原理將復值函數轉變為實值函數。
從而求得不相關的函數,得到通解。
推導過程見下圖:
)及疊加原理將復值函數轉變為實值函數。
從而求得不相關的函數,得到通解。
推導過程見下圖:


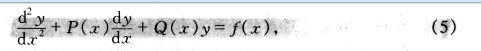
 線性的概念定義為:
線性的概念定義為:

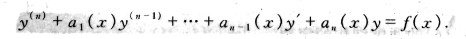 1. 線性微分方程的解的結構
1. 線性微分方程的解的結構
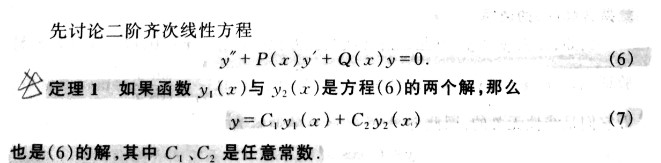 目前,式(7)不是(6)的通解。如何保證通解呢,首先引入函數組線性無關的概念:
目前,式(7)不是(6)的通解。如何保證通解呢,首先引入函數組線性無關的概念:


 下面討論二階非齊次線性方程,非齊次方程的解是齊次方程的通解加上非齊次方程的一個特解構成的。
下面討論二階非齊次線性方程,非齊次方程的解是齊次方程的通解加上非齊次方程的一個特解構成的。

 這一定理稱為線性微分方程的解的疊加原理。
這一定理稱為線性微分方程的解的疊加原理。
以上研究的是高階線性微分方程的解的結構,下面介紹解法,首先討論二階常系數齊次線性微分方程的解法





![]()

高階線性微分方程-常微分方程
