常微分方程

　　含有未知函數的導數，如

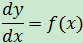
　　的方程是微分方程。 一般的，凡是表示未知函數、未知函數的導數與自變量之間的關系的方程，叫做微分方程。未知函數是一元函數的，叫常微分方程；未知函數是多元函數的叫做偏微分方程。本文主要介紹常微分方程。

　　概念往往令人迷惑，還是看看實際的例子：

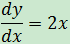
　　目標是求解x和y的關系。將等式轉換：

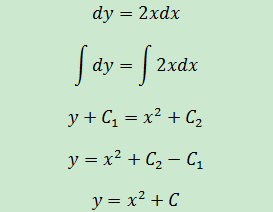
　　這就是最終答案。

　　實際上，常微分的求解過程就是利用不定積分的知識：

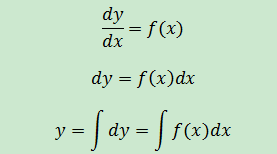
分離變量

　　分離變量是求解常微分方程的一種方法，適用於dy/dx = f(x)g(y)的形式。先看下面的示例：

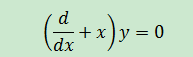
　　在物理學中它有一個專有名稱，叫做“淹沒算符”。此處沒必要去糾結物理學概念，僅需要在數學上求解這個方程。但這個表達式和以往所見的微分表達式不一樣，首先將方程展開，將其轉換為我們熟悉的形式：

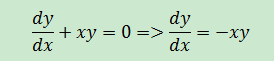
　　想要求解方程，需要繼續轉換：

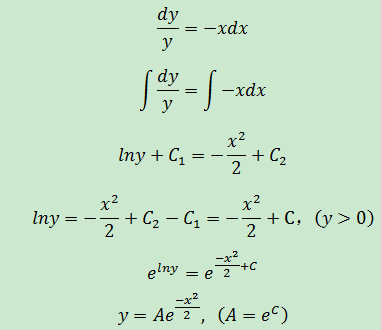
　　這就是求得的答案。

　　但上述答案只求解了y>0的情況，y≤0時尚未考慮。可以通過求導來驗證答案是否是通解：

　　令a為任意常數，將解轉換為y=ae^{-x^2}/2，當a≠0時，實際上a=±A

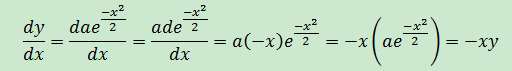
　　答案是通解，最終答案是y=ae^{-x^2}/2，a是任意常數。

　　實際上該答案就是正態分布函數，也就是著名的高斯函數，其原型：

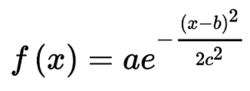
　　其中a,b,c∈R

　　高斯函數的圖形在形狀上像一個倒懸著的鐘。a表示得到曲線的高度，b是指曲線中心線在x軸的偏移，c半峰寬度（函數峰值一半處相距的寬度）。

　　當b=0,c=0,a=5時，圖像如下：

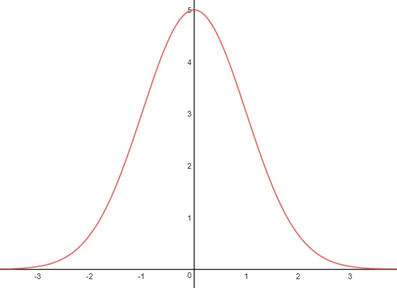
y=ae^{-x^2}/2

示例

示例1

　　曲線切線與經過原點的直線相交，曲線在交點的切線是直線斜率的兩倍，求曲線表達式。

　　首先將上述文字轉換為方程，設交點是(x,y)，曲線是y=f(x)，則曲線切線的斜率為y’，直線斜率為y/x，於是得到下面關系式：

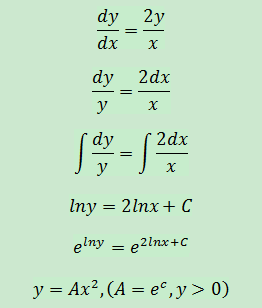
　　通過驗證尋找通解，設a=±A，則a為非零的任意常數，y=ax²，驗證該解：

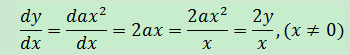
　　答案符合最初等式。最終結果是y=ax²，a∈R，x≠0

　　當a=1時，曲線y= x²，y’=2x；則在(2,4)點的切線斜率是4，切線是y=4x+b；將(2,4)代入切線，4=4×2+b，b=-4，在(2,4)點的切線為y=4x-4。下圖是滿足條件的曲線：

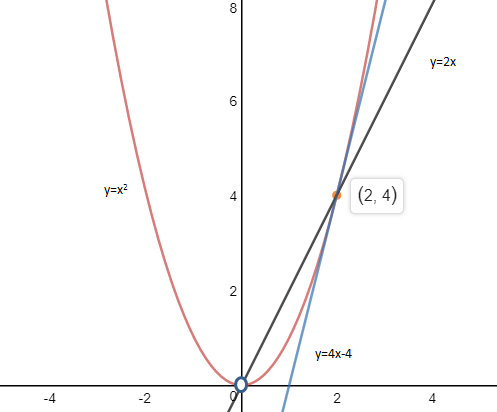
　　y=ax²實際上是一族曲線：

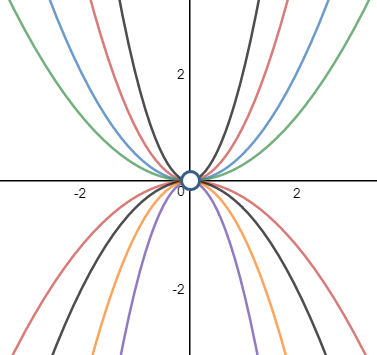
y=ax²

示例2

　　微分方程xdy/dx = (x²+x)(y²+1)，求y=f(x)

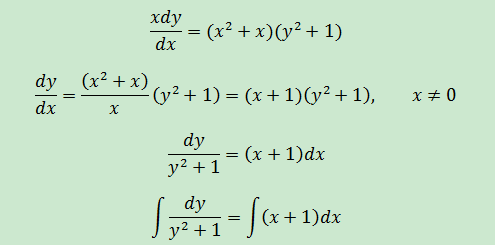
　　此處需要復習一下三角函數的求導公式：

　　由上面的公式15，

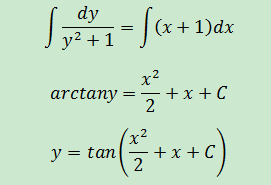
　　驗證，已知三角函數公式tan²x+1=sec²x

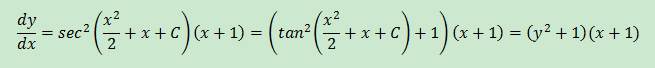
示例3

　　d²y/dx²=6x，求y=f(x)，y=f(x)在(1,1)點有水平切線。

　　題目中涉及到二階導數和一個限制條件。

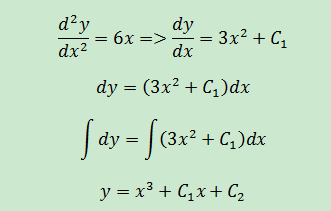
　　通過限制條件得知：

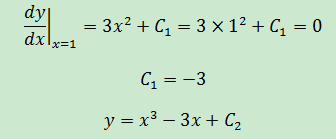
　　將(1,1)代入上式，1 = 1 – 3 + C₂，C₂ = 3

　　最終，y = x³ – 3x + 3

總結

1. 使用不定積分求解常微分方程
2. 分離變量是求解常微分方程的一種方法，適用於dy/dx = f(x)g(y)的形式

　　作者：我是8位的

　　出處：http://www.cnblogs.com/bigmonkey

　　本文以學習、研究和分享為主，如需轉載，請聯系本人，標明作者和出處，非商業用途！

數學筆記12——常微分方程和分離變量