題目：HDU 3037

題意：有n個樹，m個堅果，放到n個樹裏，可以不放完，有多少種方法。

分析：

得到組合數了。

大組合數什麽費馬小定理，Lucas定理都來了；

總的說，不能用二維地推了，用的卻是組合數的定義。

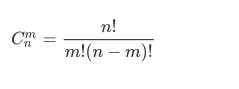
一般來說大組合通常要取模。

那麽不能邊乘邊模，邊除邊模，等式不會成立。

根據逆元，除以一個數取模 = 乘以這個數對mod的逆元。

那麽式子就可以寫成：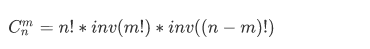

這裏，我們可以預處理所有 i 對 mod 的逆元後，累乘，這樣得到的就是階乘的逆元。

然後就是求 i 對 mod 的逆元了，什麽擴展歐幾裏得就來了。

當然，有費馬小定理。

inv[i] = (mod-mod/i)*inv[mod%i]%mod；

整個求大組合數就是這樣出來了。

void init() {

    fac[0] = 1;
    for(int i=1;i<maxn;i++)
        fac[i] = i*fac[i-1]%mod;

    inv[0] = inv[1] = 1;
    for(int i=2;i<maxn;i++)
        inv[i] = (ll)(mod-mod/i)*inv[mod%i]%mod;

    for(int i=2;i<maxn;i++)
        inv[i] = inv[i-1]*inv[i]%mod;

}

ll C(ll n,ll m) {

    
 
if(n<m)
        return 0;
    return fac[n]*inv[m]%mod*inv[n-m]%mod;

}

但是這個題目n,m的範圍驚人1000000000，作為階乘，逆元，數組開不下。

Lucas來了：

看結果吧：

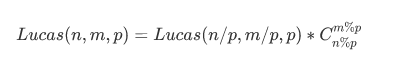
還是有組合數，用了費馬定理：

fac[n]*Inv(fac[m])%P*Inv(fac[n-m])%P；

因為這裏的對P的逆元 Inv已經不能用數組表示和地推了，Inv()函數，利用了費馬定理，快速冪等等，原理很復雜了，哈哈~~~，我就不證明了。

void initFac(int n) {
    fac[
 
0] = 1;
    for(int i=1;i<=n;i++)
        fac[i] = i*fac[i-1]%P;
}

ll Pow(ll a,int b) {
    ll re = 1;
    for(;b;b>>=1,a=a*a%P)
        if(b&1) re = re*a%P;
    return re;
}

ll Inv(ll a) {
    return Pow(a,P-2);
}

ll C(ll n,ll m) {
    if(n<m) return 0;
    return fac[n]*Inv(fac[m])%P*Inv(fac[n-m])%P;
}

ll Lucas(ll n,ll m) {
    if(n<m) return 0;
    ll re = 1;
    for(;m;n/=P,m/=P)
        re = re*C(n%P,m%P)%P;
    return re;
}

Lucas 大組合數