拉格朗日乘數法是用來求條件極值的，極值問題有兩類，其一，求函數在給定區間上的極值，對自變量沒有其它要求，這種極值稱為無條件極值。

其二，對自變量有一些附加的約束條件限制下的極值，稱為條件極值。例如給定橢球：

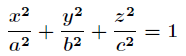
求這個橢球的內接長方體的最大體積。這個問題實際上就是條件極值問題，即在條件：

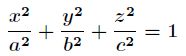
下，求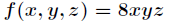的最大值。

　　當然這個問題實際可以先根據條件消去，然後帶入轉化為無條件極值問題來處理。但是有時候這樣做很困難，甚至是做不到的，

這時候就需要用拉格朗日乘數法了。如下描述：

　　求函數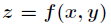在滿足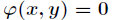下的條件極值，可以轉化為函數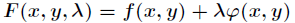的無條件極值問題。

如果是函數的駐點，則就是條件極值的嫌疑點。

回到上面的題目，通過拉格朗日乘數法將問題轉化為：

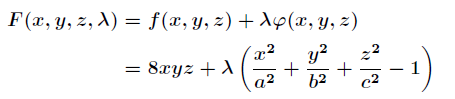
對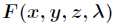求偏導得到：

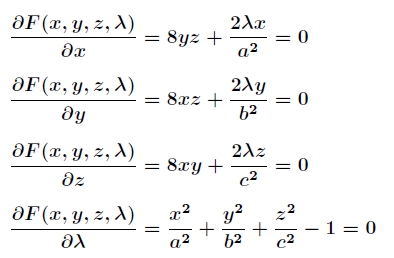
聯立前面三個方程得到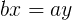和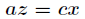，帶入第四個方程解之：

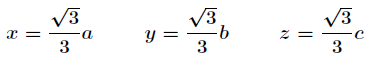
帶入解得最大體積為：

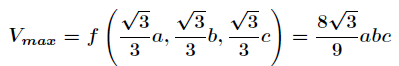
拉格朗日乘數法對一般多元函數在多個附加條件下的條件極值問題也適用。例如：

題目：求旋轉拋物面與平面的交線上到坐標原點最近的點與最遠的點。

分析：設，令的所有

偏導數為零，得到

解得兩個嫌疑點分別為

由於

所以，與原點最近的點是，最遠的點是

拉格朗日乘數法