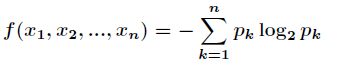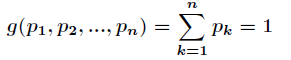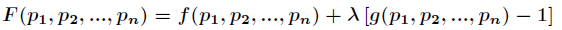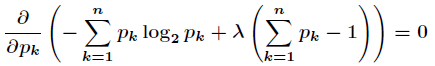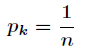[Math & Algorithm] 拉格朗日乘數法

原文來自部落格園使用者【Poll的筆記 】，僅作部分表達修改。原文地址：http://www.cnblogs.com/maybe2030/p/4946256.html

　　拉格朗日乘數法（Lagrange Multiplier Method）之前聽數學老師授課的時候就是一知半解，現在越發感覺拉格朗日乘數法應用的廣泛性，所以特意抽時間學習了麻省理工學院的線上數學課程。新學到的知識一定要立刻記錄下來，希望對各位博友有些許幫助。

1. 拉格朗日乘數法的基本思想

　　作為一種優化演算法，拉格朗日乘子法主要用於解決約束優化問題，它的基本思想就是通過引入拉格朗日乘子來將含有n個變數和k個約束條件的約束優化問題轉化為含有（n+k）個變數的無約束優化問題。拉格朗日乘子背後的數學意義是其為約束方程梯度線性組合中每個向量的係數。

　　如何將一個含有n個變數和k個約束條件的約束優化問題轉化為含有（n+k）個變數的無約束優化問題？拉格朗日乘數法從數學意義入手，通過引入拉格朗日乘子建立極值條件，對n個變數分別求偏導對應了n個方程，然後加上k個約束條件（對應k個拉格朗日乘子）一起構成包含了（n+k）變數的（n+k）個方程的方程組問題，這樣就能根據求方程組的方法對其進行求解。

　　解決的問題模型為約束優化問題：

　　min/max a function f(x,y,z), where x,y,z are not independent and g(x,y,z)=0.

　　即：min/max f(x,y,z)

　　　　s.t. g(x,y,z)=0

2. 數學例項

　　首先，我們先以麻省理工學院數學課程的一個例項來作為介紹拉格朗日乘數法的引子。

　　【麻省理工學院數學課程例項】求雙曲線xy=3上離原點最近的點。

　　解：

　　首先，我們根據問題的描述來提煉出問題對應的數學模型，即：

　　min f(x,y)=x²+y²（兩點之間的歐氏距離應該還要進行開方，但是這並不影響最終的結果，所以進行了簡化，去掉了平方）

　　s.t. xy=3.

　　根據上式我們可以知道這是一個典型的約束優化問題，其實我們在解這個問題時最簡單的解法就是通過約束條件將其中的一個變數用另外一個變數進行替換，然後代入優化的函式就可以求出極值。我們在這裡為了引出拉格朗日乘數法，所以我們採用拉格朗日乘數法的思想進行求解。

　　我們將x²+y²=c的曲線族畫出來，如下圖所示，當曲線族中的圓與xy=3曲線進行相切時，切點到原點的距離最短。也就是說，當f(x,y)=c的等高線和雙曲線g(x,y)相切時，我們可以得到上述優化問題的一個極值（注意：如果不進一步計算，在這裡我們並不知道是極大值還是極小值）。

　　現在原問題可以轉化為求當f(x,y)和g(x,y)相切時，x,y的值是多少？

　　如果兩個曲線相切，那麼它們的切線相同，即法向量是相互平行的，▽f//▽g.

　　由▽f//▽g可以得到，▽f=λ*▽g。

　　這時，我們將原有的約束優化問題轉化為了一種對偶的無約束的優化問題，如下所示：

　　原問題：min f(x,y)=x²+y²              對偶問題：由▽f=λ*▽g得，

　　　　　　s.t. xy=3                                       f_x=λ*g_x，

　　                                                                   f_y=λ*g_y，

                                                                          xy=3.

                  約束優化問題                                   無約束方程組問題

　　通過求解右邊的方程組我們可以獲取原問題的解，即

　　2x=λ*y

　　2y=λ*x

　　xy=3

　　通過求解上式可得，λ=2或者是-2；當λ=2時，(x,y)=(sqrt(3), sqrt(3))或者(-sqrt(3), -sqrt(3))，而當λ=-2時，無解。所以原問題的解為(x,y)=(sqrt(3), sqrt(3))或者(-sqrt(3), -sqrt(3))。

　　通過舉上述這個簡單的例子就是為了體會拉格朗日乘數法的思想，即通過引入拉格朗日乘子(λ)將原來的約束優化問題轉化為無約束的方程組問題。

3. 拉格朗日乘數法的基本形態

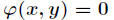 　　求函式在滿足下的條件極值，可以轉化為函式的無條件極值問題。

　　我們可以畫圖來輔助思考。

　　綠線標出的是約束g(x,y)=c的點的軌跡。藍線是f(x,y)的等高線。箭頭表示斜率，和等高線的法線平行。

　　從圖上可以直觀地看到在最優解處，f和g的斜率平行。

　　▽[f(x,y)+λ(g(x,y)−1)]=0, λ≠0

　　一旦求出λ的值，將其套入下式，易求在無約束極值和極值所對應的點。

　　F(x,y)=f(x,y)+λ(g(x,y)−c)

　　新方程F(x,y)在達到極值時與f(x,y)相等，因為F(x,y)達到極值時g(x,y)−c總等於零。

　　上述式子取得極小值時其導數為0，即▽f(x)+▽∑λ_ig_i(x)=0，也就是說f(x)和g(x)的梯度共線。

　　題目1：

　　給定橢球

     

　　求這個橢球的內接長方體的最大體積。這個問題實際上就是條件極值問題，即在條件   

    

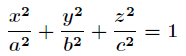
　　下，求的最大值。

　　當然這個問題實際可以先根據條件消去，然後帶入轉化為無條件極值問題來處理。但是有時候這樣做很困難，甚至是做不到的，這時候就需要用拉格朗日乘數法了。通過拉格朗日乘數法將問題轉化為

     

　　對求偏導得到

     

　　聯立前面三個方程得到和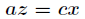，帶入第四個方程解之

      

　　帶入解得最大體積為

      

　　拉格朗日乘數法對一般多元函式在多個附加條件下的條件極值問題也適用。

　　題目2：

　　題目：求離散分佈的最大熵。

　　分析：因為離散分佈的熵表示如下

     

     而約束條件為

     

     要求函式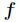的最大值，根據拉格朗日乘數法，設

     

     對所有的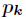求偏導數，得到

     

     計算出這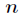個等式的微分，得到

     

     這說明所有的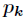都相等，最終解得

     

     因此，使用均勻分佈可得到最大熵的值。

4. 拉格朗日乘數法與KKT條件

　　我們上述討論的問題均為等式約束優化問題，但等式約束並不足以描述人們面臨的問題，不等式約束比等式約束更為常見，大部分實際問題的約束都是不超過多少時間，不超過多少人力，不超過多少成本等等。所以有幾個科學家拓展了拉格朗日乘數法，增加了KKT條件之後便可以用拉格朗日乘數法來求解不等式約束的優化問題了。

　　首先，我們先介紹一下什麼是KKT條件。

　　KKT條件是指在滿足一些有規則的條件下, 一個非線性規劃(Nonlinear Programming)問題能有最優化解法的一個必要和充分條件. 這是一個廣義化拉格朗日乘數的成果. 一般地, 一個最優化數學模型的列標準形式參考開頭的式子, 所謂 Karush-Kuhn-Tucker 最優化條件，就是指上式的最優點x^∗必須滿足下面的條件:

　　1). 約束條件滿足g_i(x^∗)≤0,i=1,2,…,p, 以及,hj(x^∗)=0,j=1,2,…,q

　　2). ∇f(x^∗)+∑_i=1μ_i∇g_i(x^∗)+∑_j=1λ_j∇h_j(x^∗)=0, 其中∇為梯度運算元;

　　3). λ_j≠0且不等式約束條件滿足μ_i≥0,μ_ig_i(x^∗)=0,i=1,2,…,p。

　　KKT條件第一項是說最優點x^∗必須滿足所有等式及不等式限制條件, 也就是說最優點必須是一個可行解, 這一點自然是毋庸置疑的. 第二項表明在最優點x^∗, ∇f必須是∇g_i和∇h_j的線性組合, μ_i和λ_j都叫作拉格朗日乘子. 所不同的是不等式限制條件有方向性, 所以每一個μ_i都必須大於或等於零, 而等式限制條件沒有方向性，所以λ_j沒有符號的限制, 其符號要視等式限制條件的寫法而定.

　　為了更容易理解，我們先舉一個例子來說明一下KKT條件的由來。

　　let L(x,μ)=f(x)+∑_k=1μ_kg_k(x)，其中μ_k≥0,g_k(x)≤0

　　∵μ_k≥0 g_k(x)≤0  =>  μ_g(x)≤0

　　∴max_μL(x,μ)=f(x)                  (2)

　　∴min_xf(x)=min_xmax_μL(x,μ)     (3)

　　max_μmin_xL(x,μ)=max_μ[min_xf(x)+min_xμg(x)]=max_μmin_xf(x)+max_μmin_xμg(x)=min_xf(x)+max_μmin_xμg(x)

　　又∵μ_k≥0, g_k(x)≤0

　　

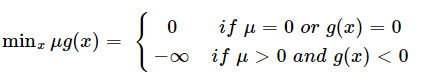
　　∴max_μmin_xμg(x)=0, 此時μ=0 or g(x)=0.

　　∴max_μmin_xL(x,μ)=min_xf(x)+max_μmin_xμg(x)=min_xf(x)      (4) 　　此時μ=0 or g(x)=0. 　　聯合(3),(4)我們得到min_xmax_μL(x,μ)=max_μmin_xL(x,μ), 亦即

 　　

　　min_xmax_μL(x,μ)=max_μmin_xL(x,μ)=min_xf(x)

　　我們把max_μmin_xL(x,μ)稱為原問題min_xmax_μL(x,μ)的對偶問題，上式表明當滿足一定條件時原問題、對偶的解、以及min_xf(x)是相同的，且在最優解x^∗處μ=0 or g(x^∗)=0。把x^∗代入(2)得max_μL(x^∗,μ)=f(x^∗)，由(4)得max_μmin_xL(x,μ)=f(x^∗)，所以L(x^∗,μ)=min_xL(x,μ)，這說明x^∗也是L(x,μ)的極值點，即

　　

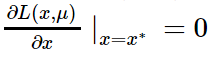
　　最後總結一下：

　　

　　KKT條件是拉格朗日乘子法的泛化，如果我們把等式約束和不等式約束一併納入進來則表現為：

　　

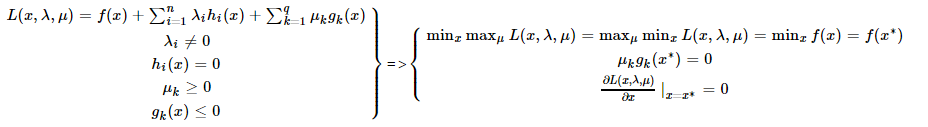
　　注：x,λ,μ都是向量。

　　

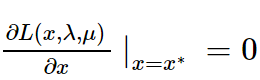
　　表明f(x)在極值點x^∗處的梯度是各個h_i(x^∗)和g_k(x^∗)梯度的線性組合。