運用二維降維到一維的例子幫助理解

對於如下二維資料

PCA演算法會試圖尋找一條直線使得所有資料到這個直線的距離的平方和最小（”投影誤差“最小）（圖中所有藍色線長度的平方和）（注意：做PCA之前需要將資料進行標準化，將資料對映到（0，1）區間內）

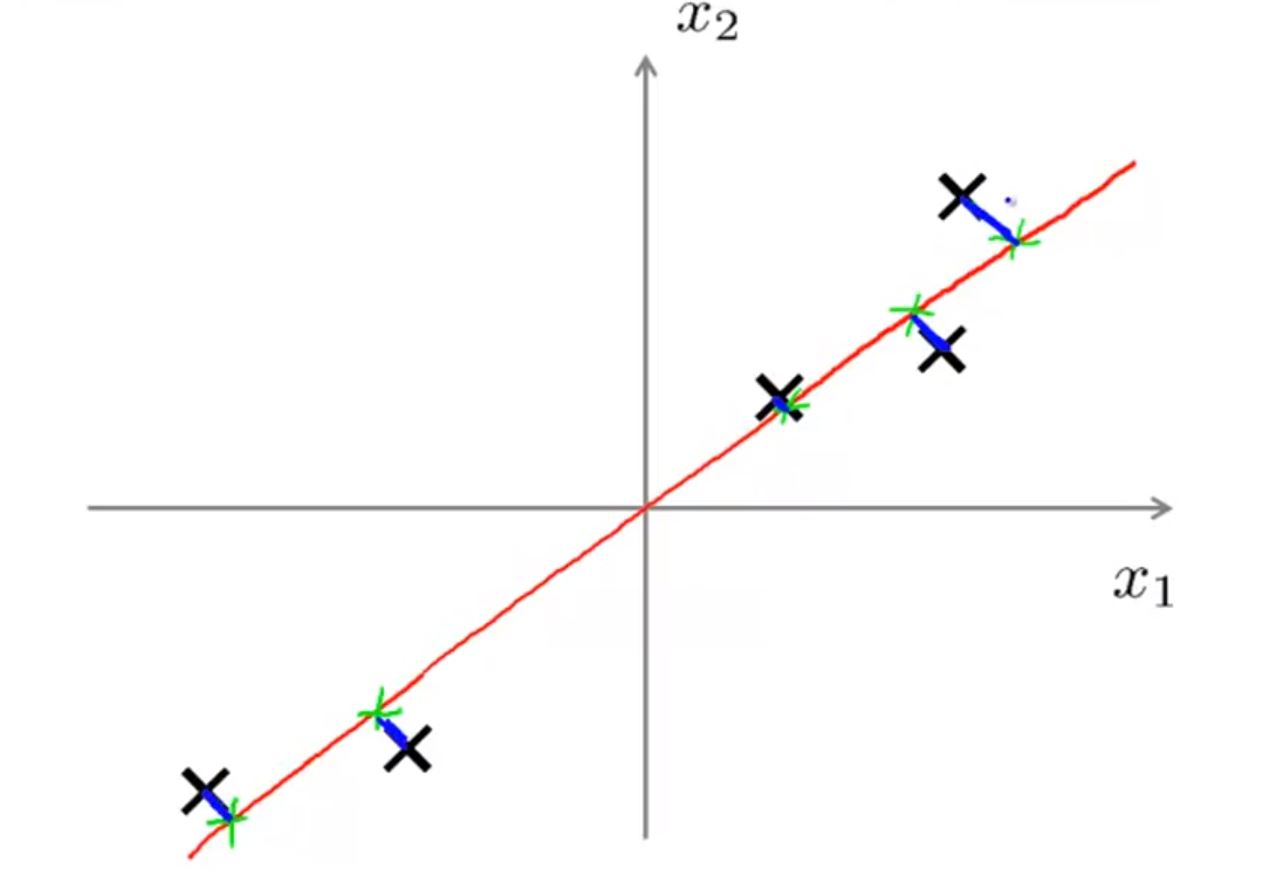
對於以下兩種情況，PCA會選擇紅色線

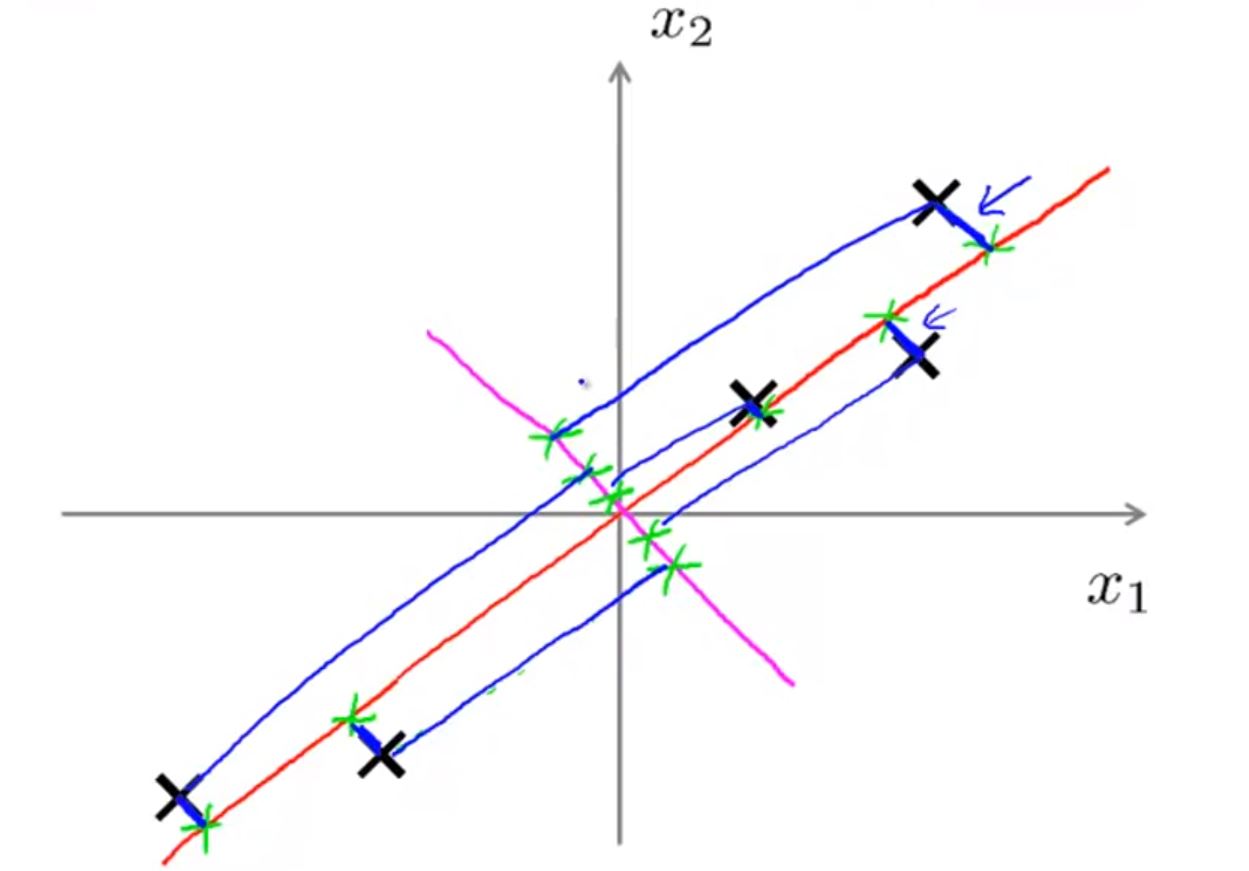
更書面的表達

Reduce from 2-dimension to 1-dimension: Find a direction (a vector u⁽¹⁾) onto which to project the data so as to minimize the projection error.

對於將二維資料降維到一維，PCA試圖尋找一個向量使得所有資料投影到這個向量上後有最小的”投影誤差“

Reduce from n-dimension to k-dimension: Find k vectors u⁽¹⁾, u⁽²⁾,..., u^(k) onto which to project the data, so as to minimize the projection error.

從n維減小到k維：找到投影資料的k個向量u⁽¹⁾, u⁽²⁾,..., u^(k)，以便最小化投影誤差。

PCA不是線性迴歸！

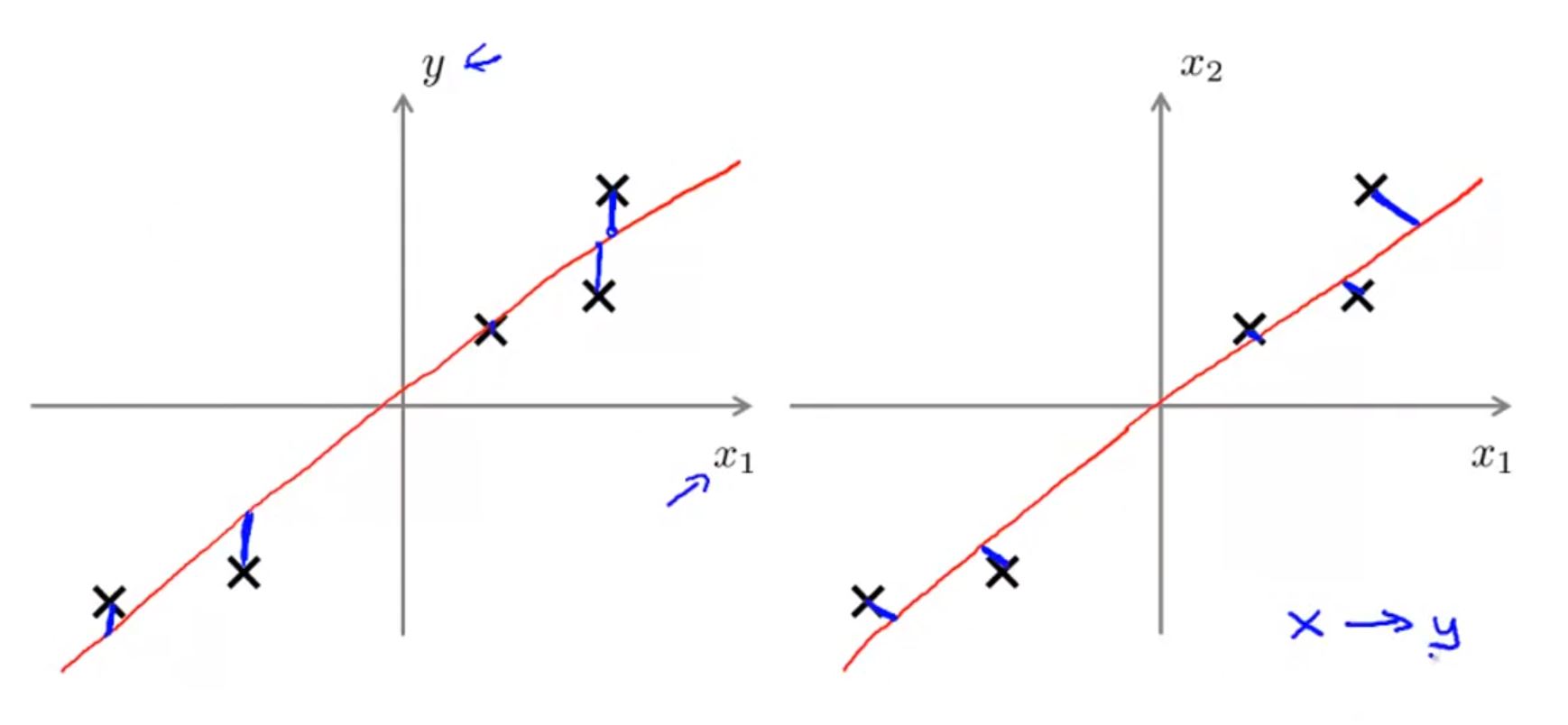
這兩個圖可能有些相似，其實有很大差異

• 線性迴歸需要根據x計算y，而PCA不需要
• 線性迴歸計算的是預測值y_pre與y的差，而PCA計算的是”投影誤差“

可以看到，PCA需要計算兩個量：k個向量u⁽¹⁾, u⁽²⁾,..., u^(k)；投影誤差。

記

\[{U_{reduce}} = \left[ {\begin{array}{*{20}{c}}
{}\\
{{u^{\left( 1 \right)}}}\\
{}
\end{array}\begin{array}{*{20}{c}}
{}\\
{{u^{\left( 2 \right)}}}\\
{}
\end{array}\begin{array}{*{20}{c}}
{}\\
{...}\\
{}
\end{array}\begin{array}{*{20}{c}}
{}\\
{{u^{\left( k \right)}}}\\
{}
\end{array}} \right]\]

因為原始資料 x 是 n x 1 的向量，投影后的 z 是 k x 1。所以 U_reduce 是 n x k 矩陣

 記

\[\begin{array}{l}
{z^{\left( i \right)}} = {U_{reduce}}^T{x^{\left( i \right)}}\\
x_{approx}^{\left( i \right)} = {U_{reduce}}{z^{\left( i \right)}}
\end{array}\]

如何選擇 k （主成分的數量）

記”平均投影誤差“

\[{\frac{1}{m}{{\sum\limits_{i = 1}^m {\left\| {{x^{\left( i \right)}} - x_{approx}^{\left( i \right)}} \right\|} }^2}}\]

記”total variation in the data“

\[{\frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}}} \right\|}^2}} }\]

則，PCA會選擇最小的 k 使得

\[\frac{{\frac{1}{m}{{\sum\limits_{i = 1}^m {\left\| {{x^{\left( i \right)}} - x_{approx}^{\left( i \right)}} \right\|} }^2}}}{{\frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}}} \right\|}^2}} }} \le 0.01\]

可以理解為降維後的資料要能代表原資料 99% 的”資訊“。（通常取 95%-99%）

 選擇 k 的具體步驟：

Try PCA with k = 1

compute 

\[{U_{reduce}}\]

\[{z^{\left( i \right)}}\]

\[x_{approx}^{\left( i \right)}\]

check if

\[\frac{{\frac{1}{m}{{\sum\limits_{i = 1}^m {\left\| {{x^{\left( i \right)}} - x_{approx}^{\left( i \right)}} \right\|} }^2}}}{{\frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}}} \right\|}^2}} }} \le 0.01?\]

increase k, back to upper.

運用PCA的建議

只在訓練集上”執行“PCA，然後將得到的”對映關係“”應用“到交叉驗證集和測試集上。

錯誤運用PCA的例子——運用PCA防止過擬合

比如將 1000 維的 x 降維到 100 維的 z，這也許能正常工作，但是這是一個不好的例子。

正確的避免過擬合的例子是正則化。

一般情況下一個標準的”機器學習系統“的設計如下：

• 獲得資料
• 執行PCA
• 執行邏輯迴歸
• 在交叉驗證集和測試集上執行

但是，建議是先不進行PCA而使用原始資料進行研究，只有當沒有PCA達不到你想要的效果時在考慮使用PCA。