[luogu P2054] [AHOI2005]洗牌

題目描述

為了表彰小聯為Samuel星球的探險所做出的貢獻，小聯被邀請參加Samuel星球近距離載人探險活動。

由於Samuel星球相當遙遠，科學家們要在飛船中度過相當長的一段時間，小聯提議用撲克牌打發長途旅行中的無聊時間。玩了幾局之後，大家覺得單純玩撲克牌對於像他們這樣的高智商人才來說太簡單了。有人提出了撲克牌的一種新的玩法。

對於撲克牌的一次洗牌是這樣定義的，將一疊N（N為偶數）張撲克牌平均分成上下兩疊，取下面一疊的第一張作為新的一疊的第一張，然後取上面一疊的第一張作為新的一疊的第二張，再取下面一疊的第二張作為新的一疊的第三張……如此交替直到所有的牌取完。

如果對一疊6張的撲克牌1 2 3 4 5 6，進行一次洗牌的過程如下圖所示：

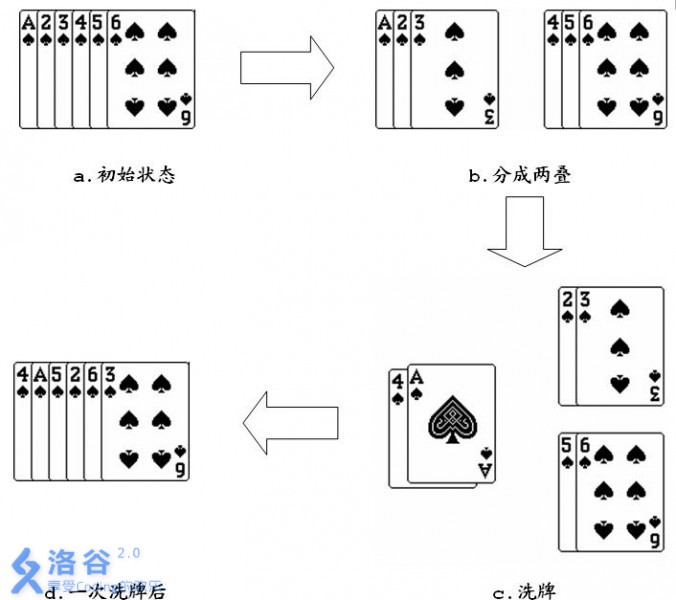
從圖中可以看出經過一次洗牌，序列1 2 3 4 5 6變為4 1 5 2 6 3。當然，再對得到的序列進行一次洗牌，又會變為2 4 6 1 3 5。

遊戲是這樣的，如果給定長度為N的一疊撲克牌，並且牌面大小從1開始連續增加到N（不考慮花色），對這樣的一疊撲克牌，進行M次洗牌。最先說出經過洗牌後的撲克牌序列中第L張撲克牌的牌面大小是多少的科學家得勝。小聯想贏取遊戲的勝利，你能幫助他嗎？

輸入輸出格式

輸入格式：

輸入文件中有三個用空格間隔的整數，分別表示N，M，L

（其中0＜N≤10^10 ，0 ≤M≤10^10，且N為偶數）。

輸出格式：

單行輸出指定的撲克牌的牌面大小。

輸入輸出樣例

6 2 3

6

說明

0＜N≤10^10 ，0 ≤M≤10^10，且N為偶數

顯然，設某張牌x當前位置為p，則洗牌一次後：

如果p<=n/2，則p變成2p；

如果p>=n/2，則p=(p-n/2)*2-1=2p-n-1=2p-(n+1)。

綜上，可發現，無論怎樣，p=2p%(n+1)。

則，m次後，原來在位置p的，現在在位置p*2^m%(n+1)。

但題目問我們位置l上是原來的幾號，則設一個方程（是x號）x*2^m≡l (mod n+1)

然後相當於解一個二元一次方程，用exgcd就可以了。

code：

 1 #include<bits/stdc++.h>
 2 #define LL long long
 3 using namespace std;
 4 LL n,m,l,k,x,y,d;
 5 LL Qpow(LL b,LL p) {
 6     if (p==0) return 1;
 7     if (p==1) return b%n;
 8     LL t=Qpow(b,p/2); t=(t*t)%n;
 9     return p%2==0?t:(t*b)%n;
10 }
11 LL exgcd(LL u,LL v,LL &x,LL &y) {
12     if (!v) {x=1,y=0; return u;}
13     LL g=exgcd(v,u%v,x,y),t;
14     t=x,x=y,y=t-(u/v)*y;
15     return g;
16 }
17 int main() {
18     cin>>n>>m>>l,n++,k=Qpow(2,m);
19     d=exgcd(k,n,x,y);
20     x=(x%n+n)%n,d=l/d*x;
21     cout<<d%n<<‘\n‘;
22     return 0;
23 }

[luogu P2054] [AHOI2005]洗牌