數論--中國剩余定理
中國剩余定理：
國務院：中國油氣人均剩余可采存儲量僅為世界平均的6%...
咳咳，不對，不是這個
中國剩余定理，又名孫子定理：
聽說過韓信點兵嗎？
韓信帶1500名兵士打仗，戰死四五百人，站3人一排，多出2人；站5人一排，多出4人；站7人一排，多出6人。韓信很快說出人數：1049。
韓信一定是讀過《孫子算經》的，
書裏面有這樣一道算術題：“今有物不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？”
也就是：
一堆物品，
3個3個分剩2個，
5個5個分剩3個，
7個7個分剩2個，
問這個物品有多少個？
解這題，我們需要構造一個答案
我們需要構造這個答案
5*7*inv(5*7, 3) % 3 = 1
3*7*inv(3*7, 5) % 5 = 1
3*5*inv(3*5, 7) % 7 = 1
這3個式子對不對，別告訴我逆元你忘了(*′?｀*)，忘了的人請翻閱前幾章復習
然後兩邊同乘你需要的數
2 * 5*7*inv(5*7, 3) % 3 = 2
3 * 3*7*inv(3*7, 5) % 5 = 3
2 * 3*5*inv(3*5, 7) % 7 = 2
令
a = 2 * 5*7*inv(5*7, 3)
b = 3 * 3*7*inv(3*7, 5)
c = 2 * 3*5*inv(3*5, 7)
那麽
a % 3 = 2
b % 5 = 3
c % 7 = 2
其實答案就是a+b+c
因為
a%5 = a%7 = 0 因為a是5的倍數，也是7的倍數
b%3 = b%7 = 0 因為b是3的倍數，也是7的倍數
c%3 = c%5 = 0 因為c是3的倍數，也是5的倍數
所以
(a + b + c) % 3 = (a % 3) + (b % 3) + (c % 3) = 2 + 0 + 0 = 2
(a + b + c) % 5 = (a % 5) + (b % 5) + (c % 5) = 0 + 3 + 0 = 3
(a + b + c) % 7 = (a % 7) + (b % 7) + (c % 7) = 0 + 0 + 2 = 2
你看你看，答案是不是a+b+c(??ω?)??，完全滿足題意
但是答案，不只一個，有無窮個，每相隔105就是一個答案（105 = 3 * 5 * 7）
根據計算，答案等於233,233%105 = 23
如果題目問你最小的那個答案，那就是23了
（233怎麽算的呢？
a=2*5*7*2=140;
b=3*3*7*1=63;
c=2*3*5*1=30;
140+63+30=233;
hhh2333333333333333,答案233出來了吧，hhh,不會算逆元的小夥伴該回去復習逆元了！）
以下抄自百度百科
中國剩余定理給出了以下的一元線性同余方程組：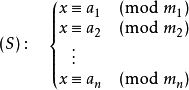
中國剩余定理說明：假設整數m1,m2, ... ,mn兩兩互質，則對任意的整數：a1,a2, ... ,an，
方程組(S)
有解，並且通解可以用如下方式構造得到：
設
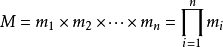是整數m1,m2, ... ,mn的乘積，並設
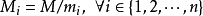是除了mi以外的n- 1個整數的乘積。
設
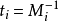這個就是逆元了
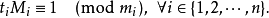通解形式為
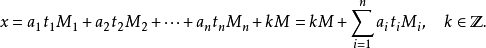在模M的意義下，方程組(S)只有一個解：
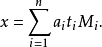那麽代碼來了：
1 #include<cstdio> 2 3 typedef long long LL; 4 5 LL inv(LL t, LL p) {//求t關於p的逆元 6 if(t>=p) 7 t=t%p; 8 return t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p; 9 } 10 11 //n個方程：x=a[i](mod m[i]) (0<=i<n) 12 LL china(int n, LL m[], LL a[]){ 13 LL M = 1, ret = 0; 14 for(int i = 0; i < n; i ++) M *= m[i]; 15 for(int i = 0; i < n; i ++){ 16 LL w = M / m[i]; 17 ret = (ret + w * inv(w, m[i]) * a[i]) % M; 18 } 19 return (ret + M) % M; 20 } 21 int main(){ 22 int n; 23 LL m[2000],a[2000]; 24 scanf("%d",&n); 25 for(int i=0;i<n;i++) 26 { 27 scanf("%d%d",&m[i],&a[i]); 28 } 29 printf("%lld\n",china(n,m,a)); 30 }
3個式子：
x%3=2
x%5=3
x%7=2
求x;
運行程序，輸入
3
3 2
5 3
7 2
試試看答案是不是23
告訴你一個好消息，上面這個中國剩余定理只是基礎，2333333333，是要求m數組裏面的元素兩兩互質的！
那如果不一定是呢？怎麽辦？
上模板吧：
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long LL; 5 typedef pair<LL, LL> PLL; 6 7 LL inv(LL t, LL p) {//求t關於p的逆元 8 if(t>=p) 9 t=t%p; 10 return t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p; 11 } 12 13 PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),總共n個線性方程組 14 LL x = 0, m = 1; 15 for(int i = 0; i < n; i ++) { 16 LL a = A[i] * m, b = B[i] - A[i]*x, d = __gcd(M[i], a); 17 if(b % d != 0) return PLL(0, -1);//答案不存在，返回-1 18 LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d); 19 x = x + m*t; 20 m *= M[i]/d; 21 } 22 x = (x % m + m ) % m; 23 return PLL(x, m);//返回的x就是答案，m是最後的lcm值 24 } 25 26 int main() 27 { 28 int n; 29 scanf("%d",&n); 30 LL a[2017],b[2017],m[2017]; 31 for(int i=0;i<n;i++) 32 { 33 scanf("%d%d%d",&a[i],&b[i],&m[i]); 34 } 35 PLL pa=linear(a,b,m,n); 36 printf("%lld\n",pa.first); 37 }
1*x=2(%3)
1*x=3(%5)
1*x=2(%7)
輸入：
3
1 2 3
1 3 5
1 2 7
輸出：
23
有興趣的可以去試試這道題
poj 2891
http://poj.org/problem?id=2891
數論--中國剩余定理