討論課提綱：

• 自我介紹
• 簡單說一下回歸的主要問題，給定數據集，找出輸入和輸出之間的關系，對於一個新的輸入可以預測其輸出

• 我們將從兩個角度來討論這個問題，一個是傳統的頻率學派，利用極大似然估計進行分析，首先利用極大似然估計估計參數，並找出其與最小二乘法之間的聯系，然後從幾何角度理解最小二乘法。因為樣本數量可能會很大，所以我們將采用在線學習的方式就行。同時因為極大似然估計是有偏估計，其估計結果也與樣本有較大聯系，所以加入正則項並通過偏差-方差對誤差結果進行分解。
• 另一個是貝葉斯學派，認為目標值滿足一定的概率分布，從而估計目標值的後驗分布。這裏分為兩個步驟，第一個步驟是估計參數的後驗分布，利用假設的參數的先驗分布，和獨立采樣得到的似然函數得到參數的後驗分布。再利用參數的後驗分布結合似然函數，關於參數積分，即得到了預測分布，知道了預測分布以後，我們就可以利用期望作為對目標值的估計。得到了期望值以後，我們會發現，貝葉斯線性回歸方法還有另一種形式，即利用等價核進行估計。

• 首先介紹一下廣義線性函數，之所以稱為廣義線性函數，是因為它關於系數是滿足線性關系的，但是基函數的選擇卻可以是非線性函數。

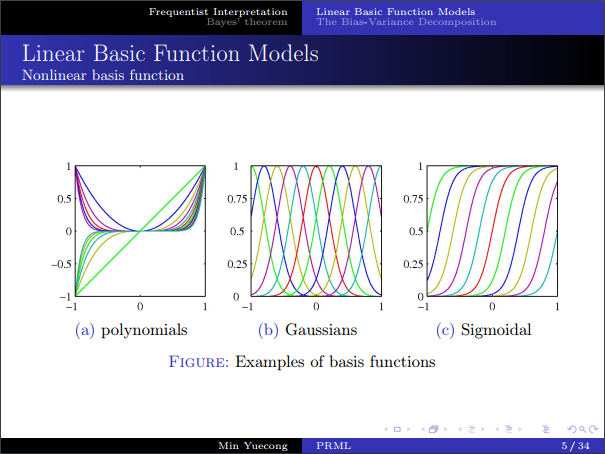
• 常用的幾種基函數，其實Taylor級數和傅裏葉級數也可以看做一種廣義線性回歸。（書上公式推導有誤，sigmoid 和 tanh 的關系）

• 回顧一下1.5節的內容，我們采用平方loss函數得到的期望損失函數，用來衡量y(x)和t之間的差距。

• 利用變分法我們可以得到損失函數的期望關於y(x)求偏導為0時對應的y(x)即是t在x的條件期望，即在y(x)=E[t|x]時，損失最小。

• 同時我們可以發現期望損失函數可以進行分解（板書推導，書上公式有誤），得到兩項，一項是噪聲而另一項則是說明在平方損失函數的條件下，最優的近似即是條件期望。
• 同時可以從平方損失函數推廣到更一般的情況。

• 現在我們開始考慮極大似然和最小二乘法之間的關系，這裏我們采用平方誤差函數。假設數據有高斯噪聲，數據是獨立采樣，從而推導出對數似然函數。

• 最大化對數似然函數實質上就是最小化平方誤差函數，求偏導得到的w的表達式，我們這是會發現，和最小二乘法的正規方程組具有相同的形式。
• 註意一下設計矩陣，每一行是一個數據，每一列是一個基函數在每個數據點上的值。
• 廣義逆矩陣（板書）

• 關於w_0和xb求偏導，得到解釋：w_0是目標均值和估計均值之間的偏差，而xb則是和目標值的殘差方差相關。

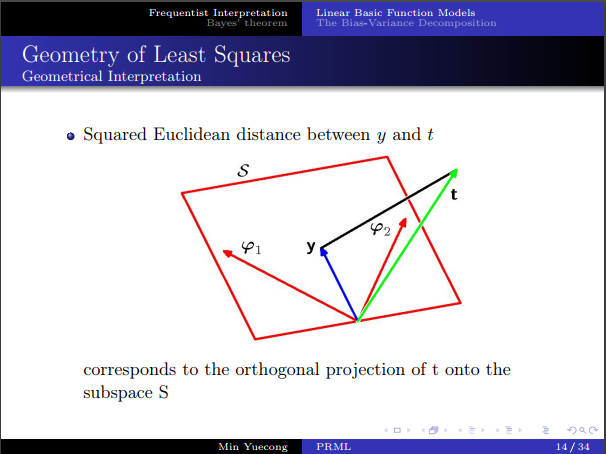
• 最小二乘的幾何解釋：子空間上的正交投影

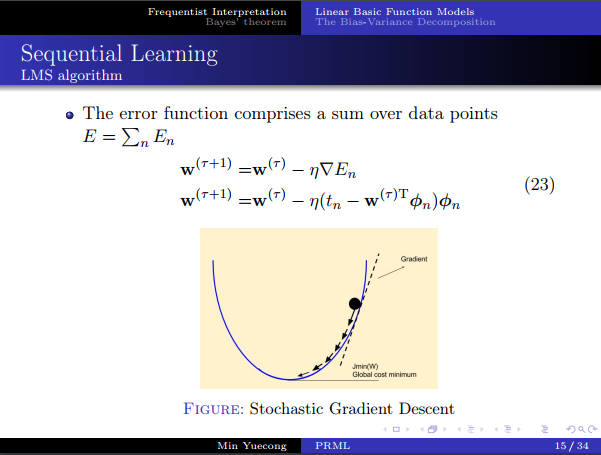
• 會註意到求逆矩陣的時候和特征維數有關，而且隨著樣本數量的增加，計算復雜性也隨之增加，所以考慮在線學習的方法。

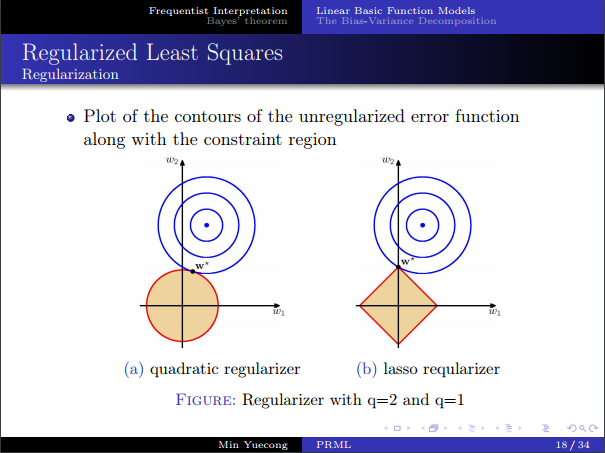
• 考慮一下正則項，可以看作一個約束問題，從幾何上看，L1正則是稀疏的，而L2正則代數性質會更好一些，之後會從貝葉斯角度對正則項再進行解釋。

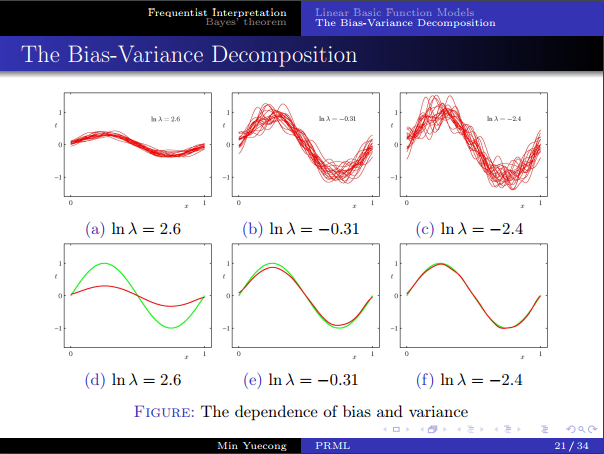
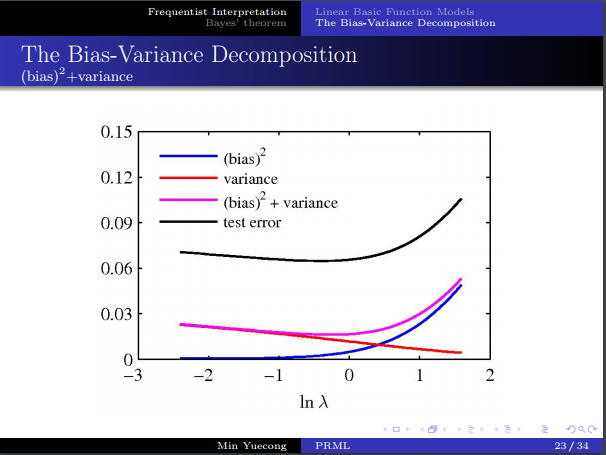
• 偏差方差分解，如果說數據無限大，則可以無限近似目標函數，但現實做不到，所以我們估計的誤差會與數據集的選取相關。
• 考慮對誤差進行分解，得到了bias和variance。
• 需要在二者之間進行權衡。

• 貝葉斯線性回歸

• 回顧一下貝葉斯公式

• 參數的後驗概率的計算

• 與帶有二次正則項的極大似然具有相同的形式。
• Laplace分布-L1正則，Gaussian分布-L2正則。

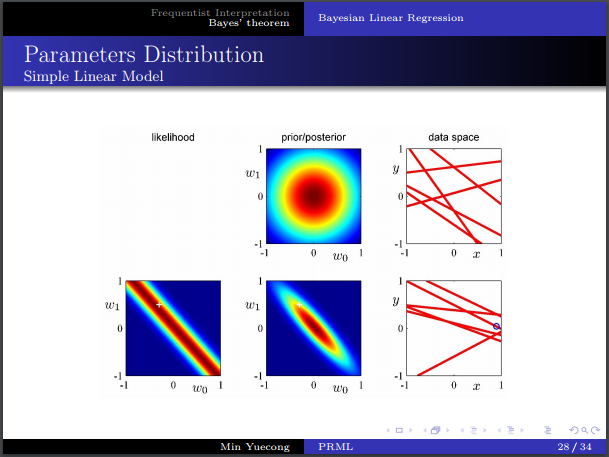
• 從圖像上理解先驗，似然和後驗，樣本對於概率分布的影響。

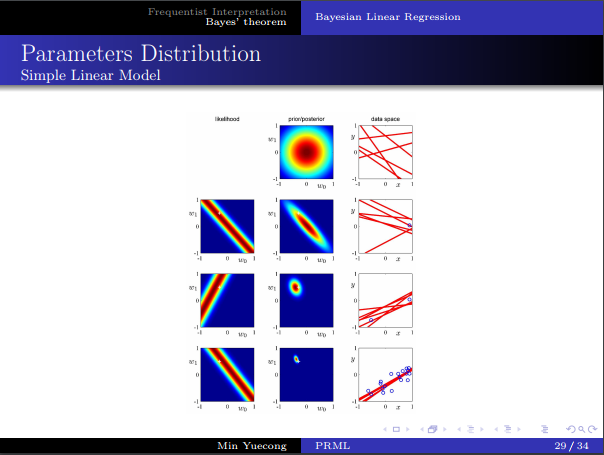
• 先驗、後驗概率的轉換，叠代的使用。

• 預測分布的推導。

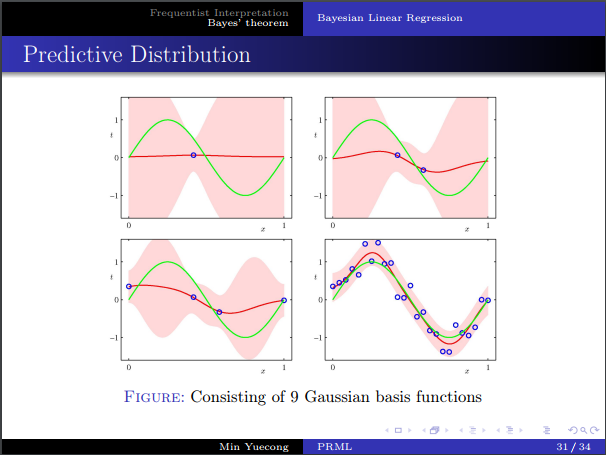
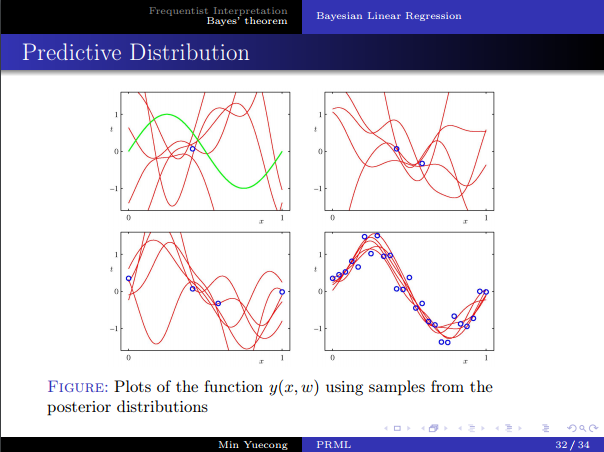
• 直觀幾何解釋。

• 等價核的定義。

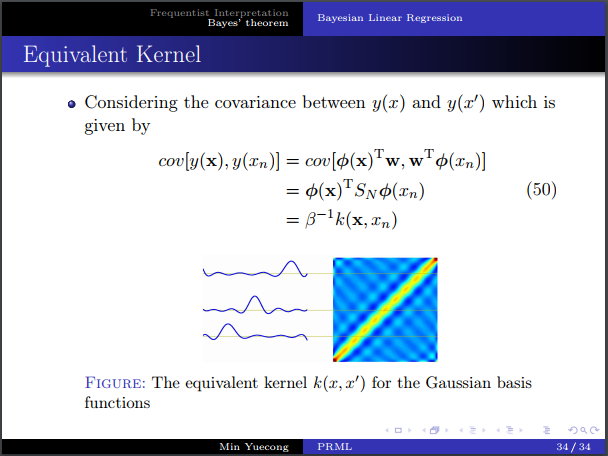
• 等價核和相關系數之間的關系。等價核和為1的推導，直觀理解，矩陣乘法。

大致整理了一下思路，希望明天晚上講的時候語速慢一點，條例清晰一點，之後再更。

Chapter3_Linear Models for Regression(討論課)