作者：桂。

時間：2017-05-22 15:28:43

鏈接：http://www.cnblogs.com/xingshansi/p/6890048.html

前言

主要記錄python工具包：sci-kit learn的基本用法。

本文主要是線性回歸模型，包括：

　　1）普通最小二乘擬合

　　2）Ridge回歸

　　3）Lasso回歸

　　4）其他常用Linear Models.

一、普通最小二乘

通常是給定數據X,y，利用參數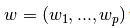進行線性擬合，準則為最小誤差：

該問題的求解可以借助：梯度下降法/最小二乘法，以最小二乘為例：

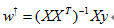
基本用法：

from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) #擬合
reg.coef_#擬合結果
reg.predict(testdata) #預測

給出一個利用training data訓練模型，並對test data預測的例子：

# -*- coding: utf-8 -*-
"""
Created on Mon May 22 15:26:03 2017

@author: Nobleding
"""

print(__doc__)


# Code source: Jaques Grobler
# License: BSD 3 clause


import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

# Load the diabetes dataset
diabetes = datasets.load_diabetes()


# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]

# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

# Create linear regression object
regr = linear_model.LinearRegression()

# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)

# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)

# The coefficients
print(‘Coefficients: \n‘, regr.coef_)
# The mean squared error
print("Mean squared error: %.2f"
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
print(‘Variance score: %.2f‘ % r2_score(diabetes_y_test, diabetes_y_pred))

# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color=‘black‘)
plt.plot(diabetes_X_test, diabetes_y_pred, color=‘blue‘, linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()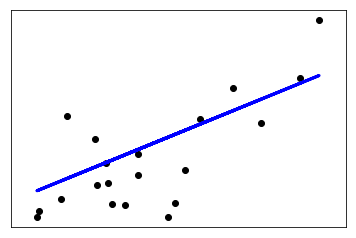

二、Ridge回歸

Ridge是在普通最小二乘的基礎上添加正則項：

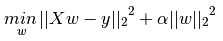
同樣可以利用最小二乘求解：

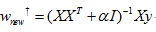
基本用法：

from sklearn import linear_model
reg = linear_model.Ridge (alpha = .5)
reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])

　 給出一個W隨α變化的例子：

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)
n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)

coefs = []
for a in alphas:
    ridge = linear_model.Ridge(alpha=a, fit_intercept=False)
    ridge.fit(X, y)
    coefs.append(ridge.coef_)

ax = plt.gca()

ax.plot(alphas, coefs)
ax.set_xscale(‘log‘)
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel(‘alpha‘)
plt.ylabel(‘weights‘)
plt.title(‘Ridge coefficients as a function of the regularization‘)
plt.axis(‘tight‘)
plt.show()

　　可以看出alpha越小，w越大：

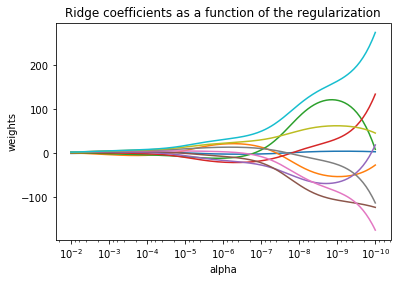
由於存在約束，何時最優呢？一個有效的方式是利用較差驗證進行選取，利用Generalized Cross-Validation (GCV)：

from sklearn import linear_model
reg = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0])
reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])       
reg.alpha_   

三、Lasso回歸

其實添加約束項可以推而廣之：

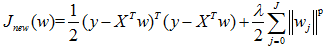
p = 2就是Ridge回歸，p = 1就是Lasso回歸。

給出Lasso的準則函數：

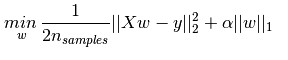
基本用法：

from sklearn import linear_model
reg = linear_model.Lasso(alpha = 0.1)
reg.fit([[0, 0], [1, 1]], [0, 1])
reg.predict([[1, 1]])

四、ElasticNet

其實就是Lasso與Ridge的折中：

基本用法：

from sklearn.linear_model import ElasticNet
enet = ElasticNet(alpha=alpha, l1_ratio=0.7)
y_pred_enet = enet.fit(X_train, y_train).predict(X_test)

　給出信號有Lasso以及ElasticNet回歸的對比：

"""
========================================
Lasso and Elastic Net for Sparse Signals
========================================

Estimates Lasso and Elastic-Net regression models on a manually generated
sparse signal corrupted with an additive noise. Estimated coefficients are
compared with the ground-truth.

"""
print(__doc__)

import numpy as np
import matplotlib.pyplot as plt

from sklearn.metrics import r2_score

###############################################################################
# generate some sparse data to play with
np.random.seed(42)

n_samples, n_features = 50, 200
X = np.random.randn(n_samples, n_features)
coef = 3 * np.random.randn(n_features)
inds = np.arange(n_features)
np.random.shuffle(inds)
coef[inds[10:]] = 0  # sparsify coef
y = np.dot(X, coef)

# add noise
y += 0.01 * np.random.normal(size=n_samples)

# Split data in train set and test set
n_samples = X.shape[0]
X_train, y_train = X[:n_samples // 2], y[:n_samples // 2]
X_test, y_test = X[n_samples // 2:], y[n_samples // 2:]

###############################################################################
# Lasso
from sklearn.linear_model import Lasso

alpha = 0.1
lasso = Lasso(alpha=alpha)

y_pred_lasso = lasso.fit(X_train, y_train).predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(lasso)
print("r^2 on test data : %f" % r2_score_lasso)

###############################################################################
# ElasticNet
from sklearn.linear_model import ElasticNet

enet = ElasticNet(alpha=alpha, l1_ratio=0.7)

y_pred_enet = enet.fit(X_train, y_train).predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(enet)
print("r^2 on test data : %f" % r2_score_enet)

plt.plot(enet.coef_, color=‘lightgreen‘, linewidth=2,
         label=‘Elastic net coefficients‘)
plt.plot(lasso.coef_, color=‘gold‘, linewidth=2,
         label=‘Lasso coefficients‘)
plt.plot(coef, ‘--‘, color=‘navy‘, label=‘original coefficients‘)
plt.legend(loc=‘best‘)
plt.title("Lasso R^2: %f, Elastic Net R^2: %f"
          % (r2_score_lasso, r2_score_enet))
plt.show()

　　Lasso比Elastic是要稀疏一些的：

五、Lasso回歸求解

實際應用中，Lasso求解是一類問題——稀疏重構（Sparse reconstrction），順便總結一下。

對於欠定方程：其中，且，此時存在無窮多解，希望求解最稀疏的解：

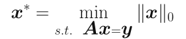
大牛們已經證明：當矩陣A滿足限制等距屬性（Restricted isometry propety, RIP）條件時，上述問題可松弛為：

RIP條件（更多細節點擊這裏）：

若y存在加性白噪聲：，則上述問題可以有三種處理形式（某種程度等效，未研究）：

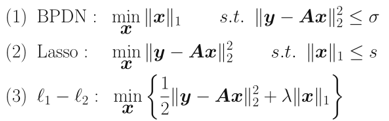
就是這幾個問題都可以互相轉化求解，以Lasso為例：這類方法很多，如投影梯度算法（Gradient Projection）、最小角回歸（LARS）算法。

六、幾種回歸的聯系

事實上，對於線性回歸模型：

y = Wx + ε

ε為估計誤差。

　　A-W為均勻分布（最小均方誤差）

也就是：

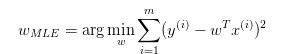
　　B-W服從高斯分布（Ridge回歸）

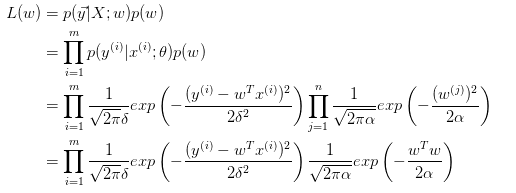
取對數：

等價於：

　　C-W服從拉普拉斯分布（Lasso回歸）

與Ridge推導類似，得出：

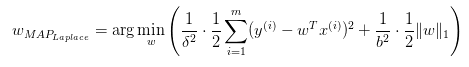
三種情況對應的約束邊界：

最小二乘：均勻分布就是無約束的情況。

Ridge：

Lasso: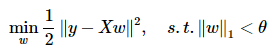

這樣對應圖形來看就更明顯了，可以看出對W的約束是越來越嚴格的。ElasticNet的情況雖然沒有分析，也容易理解：它的限定條件一定介於菱形與圓形兩邊界之間。

七、其他

更多的擬合可以看鏈接，用到了補充了，這裏列幾個以前見過的。

　　A-最小角回歸（Least Angle Regressive，LARS）

LARS算法點擊這裏。

基本用法：

from sklearn import linear_model
clf = linear_model.Lars(n_nonzero_coefs=1)
clf.fit([[-1, 1], [0, 0], [1, 1]], [-1.1111, 0, -1.1111])
print(clf.coef_) 

　　B-正交匹配追蹤（orthogonal matching pursuit, OMP）

OMP思路：

對應準則函數：

也可以寫為：

本質上是對重建信號，不斷從字典中找出最匹配的基，然後進行表達，表達後的殘差：再從字典中找基進行表達，循環往復。

停止的基本條件通常有三類：1）達到指定的叠代次數;2）殘差小於給定的門限;3）字典的任意基與殘差的相關性小於給定的門限.

基本用法：

"""
===========================
Orthogonal Matching Pursuit
===========================

Using orthogonal matching pursuit for recovering a sparse signal from a noisy
measurement encoded with a dictionary
"""
print(__doc__)

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.linear_model import OrthogonalMatchingPursuitCV
from sklearn.datasets import make_sparse_coded_signal

n_components, n_features = 512, 100
n_nonzero_coefs = 17

# generate the data
###################

# y = Xw
# |x|_0 = n_nonzero_coefs

y, X, w = make_sparse_coded_signal(n_samples=1,
                                   n_components=n_components,
                                   n_features=n_features,
                                   n_nonzero_coefs=n_nonzero_coefs,
                                   random_state=0)

idx, = w.nonzero()

# distort the clean signal
##########################
y_noisy = y + 0.05 * np.random.randn(len(y))

# plot the sparse signal
########################
plt.figure(figsize=(7, 7))
plt.subplot(4, 1, 1)
plt.xlim(0, 512)
plt.title("Sparse signal")
plt.stem(idx, w[idx])

# plot the noise-free reconstruction
####################################

omp = OrthogonalMatchingPursuit(n_nonzero_coefs=n_nonzero_coefs)
omp.fit(X, y)
coef = omp.coef_
idx_r, = coef.nonzero()
plt.subplot(4, 1, 2)
plt.xlim(0, 512)
plt.title("Recovered signal from noise-free measurements")
plt.stem(idx_r, coef[idx_r])

# plot the noisy reconstruction
###############################
omp.fit(X, y_noisy)
coef = omp.coef_
idx_r, = coef.nonzero()
plt.subplot(4, 1, 3)
plt.xlim(0, 512)
plt.title("Recovered signal from noisy measurements")
plt.stem(idx_r, coef[idx_r])

# plot the noisy reconstruction with number of non-zeros set by CV
##################################################################
omp_cv = OrthogonalMatchingPursuitCV()
omp_cv.fit(X, y_noisy)
coef = omp_cv.coef_
idx_r, = coef.nonzero()
plt.subplot(4, 1, 4)
plt.xlim(0, 512)
plt.title("Recovered signal from noisy measurements with CV")
plt.stem(idx_r, coef[idx_r])

plt.subplots_adjust(0.06, 0.04, 0.94, 0.90, 0.20, 0.38)
plt.suptitle(‘Sparse signal recovery with Orthogonal Matching Pursuit‘,
             fontsize=16)
plt.show()

　　結果圖：

　　C-貝葉斯回歸（Bayesian Regression）

其實就是將最小二乘的擬合問題轉化為概率問題：

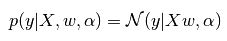
上面分析幾種回歸關系的時候，概率的部分就是貝葉斯回歸的思想。

為什麽貝葉斯回歸可以避免overfitting？MLE對應最小二乘擬合，Bayessian Regression對應有約束的擬合，這個約束也就是先驗概率。

基本用法：

clf = BayesianRidge(compute_score=True)
clf.fit(X, y)

　　代碼示例：

"""
=========================
Bayesian Ridge Regression
=========================

Computes a Bayesian Ridge Regression on a synthetic dataset.

See :ref:`bayesian_ridge_regression` for more information on the regressor.

Compared to the OLS (ordinary least squares) estimator, the coefficient
weights are slightly shifted toward zeros, which stabilises them.

As the prior on the weights is a Gaussian prior, the histogram of the
estimated weights is Gaussian.

The estimation of the model is done by iteratively maximizing the
marginal log-likelihood of the observations.

We also plot predictions and uncertainties for Bayesian Ridge Regression
for one dimensional regression using polynomial feature expansion.
Note the uncertainty starts going up on the right side of the plot.
This is because these test samples are outside of the range of the training
samples.
"""
print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

from sklearn.linear_model import BayesianRidge, LinearRegression

###############################################################################
# Generating simulated data with Gaussian weights
np.random.seed(0)
n_samples, n_features = 100, 100
X = np.random.randn(n_samples, n_features)  # Create Gaussian data
# Create weights with a precision lambda_ of 4.
lambda_ = 4.
w = np.zeros(n_features)
# Only keep 10 weights of interest
relevant_features = np.random.randint(0, n_features, 10)
for i in relevant_features:
    w[i] = stats.norm.rvs(loc=0, scale=1. / np.sqrt(lambda_))
# Create noise with a precision alpha of 50.
alpha_ = 50.
noise = stats.norm.rvs(loc=0, scale=1. / np.sqrt(alpha_), size=n_samples)
# Create the target
y = np.dot(X, w) + noise

###############################################################################
# Fit the Bayesian Ridge Regression and an OLS for comparison
clf = BayesianRidge(compute_score=True)
clf.fit(X, y)

ols = LinearRegression()
ols.fit(X, y)

###############################################################################
# Plot true weights, estimated weights, histogram of the weights, and
# predictions with standard deviations
lw = 2
plt.figure(figsize=(6, 5))
plt.title("Weights of the model")
plt.plot(clf.coef_, color=‘lightgreen‘, linewidth=lw,
         label="Bayesian Ridge estimate")
plt.plot(w, color=‘gold‘, linewidth=lw, label="Ground truth")
plt.plot(ols.coef_, color=‘navy‘, linestyle=‘--‘, label="OLS estimate")
plt.xlabel("Features")
plt.ylabel("Values of the weights")
plt.legend(loc="best", prop=dict(size=12))

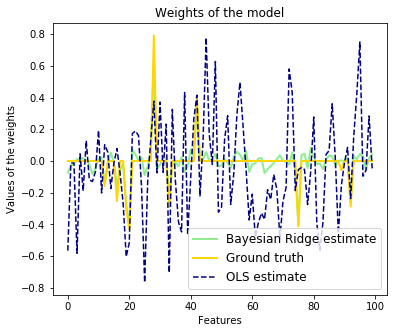
　　D-多項式回歸（Polynomial regression）

上文的最小二乘擬合可以理解成多元回歸問題。多項式回歸可以轉化為多元回歸問題。

對於

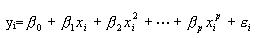
令

則

這就是多元回歸問題了。

基本用法（階數需指定）：

print(__doc__)

# Author: Mathieu Blondel
#         Jake Vanderplas
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline


def f(x):
    """ function to approximate by polynomial interpolation"""
    return x * np.sin(x)


# generate points used to plot
x_plot = np.linspace(0, 10, 100)

# generate points and keep a subset of them
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:20])
y = f(x)

# create matrix versions of these arrays
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

colors = [‘teal‘, ‘yellowgreen‘, ‘gold‘]
lw = 2
plt.plot(x_plot, f(x_plot), color=‘cornflowerblue‘, linewidth=lw,
         label="ground truth")
plt.scatter(x, y, color=‘navy‘, s=30, marker=‘o‘, label="training points")

for count, degree in enumerate([3, 4, 5]):
    model = make_pipeline(PolynomialFeatures(degree), Ridge())
    model.fit(X, y)
    y_plot = model.predict(X_plot)
    plt.plot(x_plot, y_plot, color=colors[count], linewidth=lw,
             label="degree %d" % degree)

plt.legend(loc=‘lower left‘)

plt.show()

　　E-羅傑斯特回歸（Logistic regression）

這個之前有梳理過。

L2約束（就是softmax衰減的情況）：

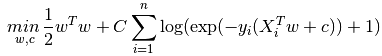
也可以是L1約束：

基本用法：

"""
==============================================
L1 Penalty and Sparsity in Logistic Regression
==============================================

Comparison of the sparsity (percentage of zero coefficients) of solutions when
L1 and L2 penalty are used for different values of C. We can see that large
values of C give more freedom to the model.  Conversely, smaller values of C
constrain the model more. In the L1 penalty case, this leads to sparser
solutions.

We classify 8x8 images of digits into two classes: 0-4 against 5-9.
The visualization shows coefficients of the models for varying C.
"""

print(__doc__)

# Authors: Alexandre Gramfort <[email protected]>
#          Mathieu Blondel <[email protected]>
#          Andreas Mueller <[email protected]>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler

digits = datasets.load_digits()

X, y = digits.data, digits.target
X = StandardScaler().fit_transform(X)

# classify small against large digits
y = (y > 4).astype(np.int)


# Set regularization parameter
for i, C in enumerate((100, 1, 0.01)):
    # turn down tolerance for short training time
    clf_l1_LR = LogisticRegression(C=C, penalty=‘l1‘, tol=0.01)
    clf_l2_LR = LogisticRegression(C=C, penalty=‘l2‘, tol=0.01)
    clf_l1_LR.fit(X, y)
    clf_l2_LR.fit(X, y)

    coef_l1_LR = clf_l1_LR.coef_.ravel()
    coef_l2_LR = clf_l2_LR.coef_.ravel()

    # coef_l1_LR contains zeros due to the
    # L1 sparsity inducing norm

    sparsity_l1_LR = np.mean(coef_l1_LR == 0) * 100
    sparsity_l2_LR = np.mean(coef_l2_LR == 0) * 100

    print("C=%.2f" % C)
    print("Sparsity with L1 penalty: %.2f%%" % sparsity_l1_LR)
    print("score with L1 penalty: %.4f" % clf_l1_LR.score(X, y))
    print("Sparsity with L2 penalty: %.2f%%" % sparsity_l2_LR)
    print("score with L2 penalty: %.4f" % clf_l2_LR.score(X, y))

    l1_plot = plt.subplot(3, 2, 2 * i + 1)
    l2_plot = plt.subplot(3, 2, 2 * (i + 1))
    if i == 0:
        l1_plot.set_title("L1 penalty")
        l2_plot.set_title("L2 penalty")

    l1_plot.imshow(np.abs(coef_l1_LR.reshape(8, 8)), interpolation=‘nearest‘,
                   cmap=‘binary‘, vmax=1, vmin=0)
    l2_plot.imshow(np.abs(coef_l2_LR.reshape(8, 8)), interpolation=‘nearest‘,
                   cmap=‘binary‘, vmax=1, vmin=0)
    plt.text(-8, 3, "C = %.2f" % C)

    l1_plot.set_xticks(())
    l1_plot.set_yticks(())
    l2_plot.set_xticks(())
    l2_plot.set_yticks(())

plt.show()

　　8X8的figure，不同C取值：

　　F-隨機梯度下降（Stochastic Gradient Descent, SGD）

梯度下降之前梳理過了。

基本用法：

from sklearn.linear_model import SGDClassifier
X = [[0., 0.], [1., 1.]]
y = [0, 1]
clf = SGDClassifier(loss="hinge", penalty="l2")
clf.fit(X, y)

　　其中涉及到：SGDClassifier，Linear classifiers (SVM, logistic regression, a.o.) with SGD training.提供了分類與回歸的應用：

The classes SGDClassifier and SGDRegressor provide functionality to fit linear models for classification and regression using different (convex) loss functions and different penalties. E.g., with loss="log", SGDClassifier fits a logistic regression model, while with loss="hinge" it fits a linear support vector machine (SVM).

以分類為例：

clf = SGDClassifier(loss="log").fit(X, y)

其中loss:

 ‘hinge‘, ‘log‘, ‘modified_huber‘, ‘squared_hinge‘,                ‘perceptron‘, or a regression loss: ‘squared_loss‘, ‘huber‘,                ‘epsilon_insensitive‘, or ‘squared_epsilon_insensitive‘

　　應用實例：

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import SGDClassifier

# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2]  # we only take the first two features. We could
                      # avoid this ugly slicing by using a two-dim dataset
y = iris.target
colors = "bry"

# shuffle
idx = np.arange(X.shape[0])
np.random.seed(13)
np.random.shuffle(idx)
X = X[idx]
y = y[idx]

# standardize
mean = X.mean(axis=0)
std = X.std(axis=0)
X = (X - mean) / std

h = .02  # step size in the mesh

clf = SGDClassifier(alpha=0.001, n_iter=100).fit(X, y)

# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))

# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
plt.axis(‘tight‘)

# Plot also the training points
for i, color in zip(clf.classes_, colors):
    idx = np.where(y == i)
    plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
                cmap=plt.cm.Paired)
plt.title("Decision surface of multi-class SGD")
plt.axis(‘tight‘)

# Plot the three one-against-all classifiers
xmin, xmax = plt.xlim()
ymin, ymax = plt.ylim()
coef = clf.coef_
intercept = clf.intercept_


def plot_hyperplane(c, color):
    def line(x0):
        return (-(x0 * coef[c, 0]) - intercept[c]) / coef[c, 1]

    plt.plot([xmin, xmax], [line(xmin), line(xmax)],
             ls="--", color=color)

for i, color in zip(clf.classes_, colors):
    plot_hyperplane(i, color)
plt.legend()
plt.show()

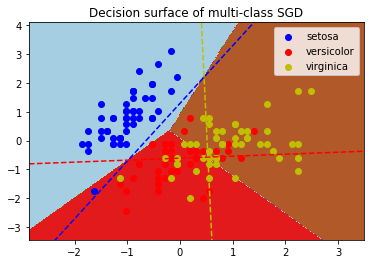
　　G-感知器（Perceptron）

之前梳理過。SGDClassifier中包含Perceptron。

　　H-隨機采樣一致（Random sample consensus, RANSAC）

之前梳理過。Ransac是數據預處理的操作。

基本用法：

ransac = linear_model.RANSACRegressor()
ransac.fit(X, y)

　　應用實例：

import numpy as np
from matplotlib import pyplot as plt

from sklearn import linear_model, datasets


n_samples = 1000
n_outliers = 50


X, y, coef = datasets.make_regression(n_samples=n_samples, n_features=1,
                                      n_informative=1, noise=10,
                                      coef=True, random_state=0)

# Add outlier data
np.random.seed(0)
X[:n_outliers] = 3 + 0.5 * np.random.normal(size=(n_outliers, 1))
y[:n_outliers] = -3 + 10 * np.random.normal(size=n_outliers)

# Fit line using all data
lr = linear_model.LinearRegression()
lr.fit(X, y)

# Robustly fit linear model with RANSAC algorithm
ransac = linear_model.RANSACRegressor()
ransac.fit(X, y)
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)

# Predict data of estimated models
line_X = np.arange(X.min(), X.max())[:, np.newaxis]
line_y = lr.predict(line_X)
line_y_ransac = ransac.predict(line_X)

# Compare estimated coefficients
print("Estimated coefficients (true, linear regression, RANSAC):")
print(coef, lr.coef_, ransac.estimator_.coef_)

lw = 2
plt.scatter(X[inlier_mask], y[inlier_mask], color=‘yellowgreen‘, marker=‘.‘,
            label=‘Inliers‘)
plt.scatter(X[outlier_mask], y[outlier_mask], color=‘gold‘, marker=‘.‘,
            label=‘Outliers‘)
plt.plot(line_X, line_y, color=‘navy‘, linewidth=lw, label=‘Linear regressor‘)
plt.plot(line_X, line_y_ransac, color=‘cornflowerblue‘, linewidth=lw,
         label=‘RANSAC regressor‘)
plt.legend(loc=‘lower right‘)
plt.xlabel("Input")
plt.ylabel("Response")
plt.show()

參考：

• http://scikit-learn.org/dev/supervised_learning.html#supervised-learning
• https://www.zhihu.com/question/23536142

Regression：Generalized Linear Models