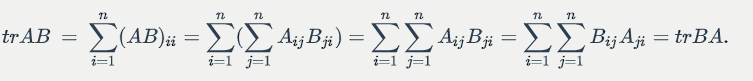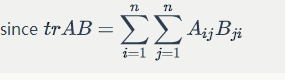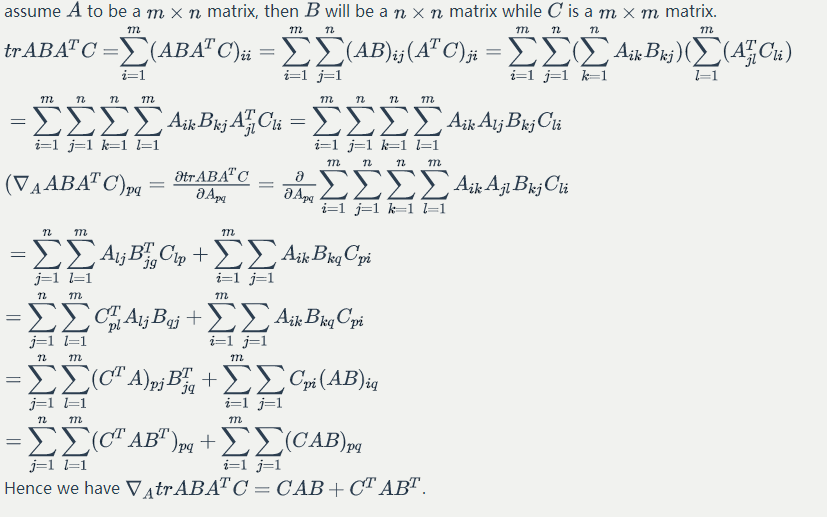CS 229 notes Supervised Learning

標簽（空格分隔）： 監督學習 線性代數

Forword

the proof of Normal equation and, before that, some linear algebra equations, which will be used in the proof.

The normal equation

Linear algebra preparation

For two matrices and such that is square, .

Proof:

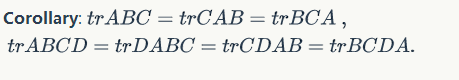
Some properties:

some facts of matrix derivative:

Proof:

Proof 1:

Proof 2:

Proof:
( refers to the cofactor)

Least squares revisited

(if we don’t include the intercept term)

since ,

Thus,
$\frac{1}{2}(X\theta-\vec{y})^T(X\theta-\vec{y}) =
\frac{1}{2}\displaystyle{\sum{i=1}^{m}(h

Combine Equations ：

Hence

Notice it is a real number, or you can see it as a matrix, so

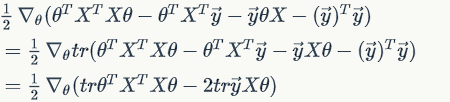
since and involves no elements.
then use equation with ，

To minmize ， we set its derivative to zero, and obtain the normal equation:

CS 229 notes Supervised Learning