一、函數的導數的引入

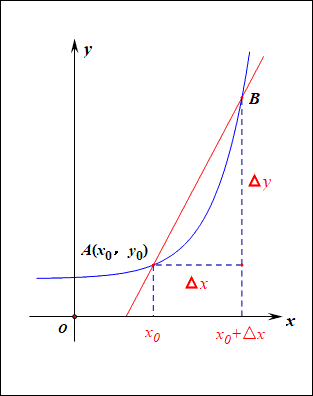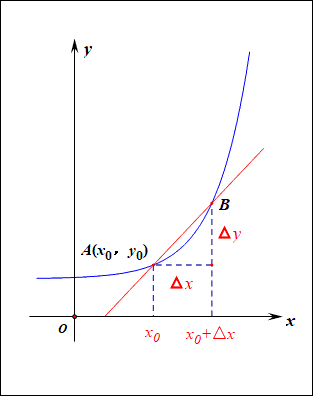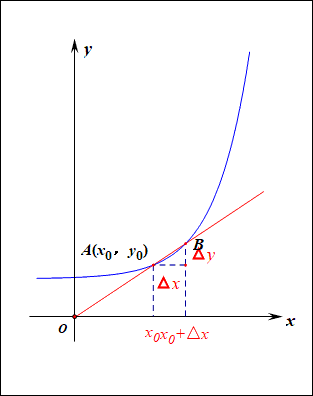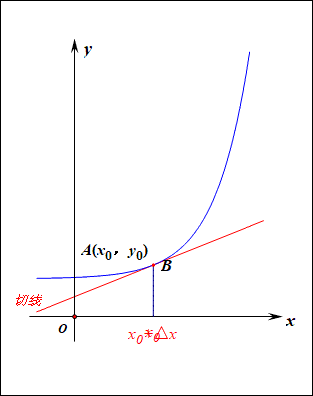
如圖所示，已知函數\(y=f(x)\)，給定其上的兩個點\(A(x_0，y_0)\)和\(B(x_0+\Delta x，y_0+\Delta y)\)，則經過這兩個點的直線\(AB\)，我們稱為函數的割線，表達式\(\cfrac{\Delta y}{\Delta x}\)稱為函數在\((x_0，x_0+\Delta x)\)上的平均變化率，也就是割線的斜率\(k=\cfrac{\Delta y}{\Delta x}\)， 當點\(B\)沿著函數圖像向點\(A\)靠近時，即\(\Delta x\longrightarrow 0\)時，割線就變成了切線，也就是平均變化率變成了瞬時變化率。

用數學式子表達如下：\(\lim\limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x}\)，我們稱為函數在點\(x=x_0\)處的瞬時變化率，如果這個極限存在，記為常數\(k\)，那麽我們就稱函數在這一點有導數，並稱之為函數在點\(x=x_0\)的導數，記作\(f'(x_0)=\lim\limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x}\)，或者記作\(y'|_{x=x_0}\)或者\(\cfrac{df(x_0)}{dx}\)

總結：

1、函數在某一點處的導數，是一個常數，其對應的形為函數在這一點的切線的斜率。即\(k=f'(x_0)=\lim\limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x}\)

2、函數在某一點有導數的前提條件是函數在這一點的極限要存在，初高中階段所學的函數中有一個函數\(y=|x|\)，在\(x=0\)處就沒有導數，即函數\(y=|x|\)在\(x=0\)處不可導，粗淺的可以這樣理解，凡是函數圖像上有尖角的地方就不可導，詳細的原因是函數在這一點處的左右極限不相等。

3、導數與幾何、代數、物理都有關聯，比如在幾何上可以求在某點處的切線斜率；在代數上可以求瞬時變化率；在物理上可以求速度和加速度(位移對時間的導數是速度，速度對時間的導數是加速度)；

4、求導和求不定積分是一對互逆的運算。

5、對函數而言，連續不一定可導，但可導一定連續。比如函數\(y=|x|\)，故函數在某個區間上連續是函數可導的必要不充分條件，因此我們給函數求導時往往先要求函數要連續。

6、過函數上某一定點的割線的極限是函數的過這一點的切線，割線的斜率的極限就是切線的斜率。

7、我們在初中定義直線和圓(圓是非常特殊的封閉圖形)相切時是利用交點的個數，當二者只有一個交點時，就一定相切；現在我們利用割線的極限來定義切線，就得註意打破這一點，比如直線\(x=1\)和拋物線\(y=(x-1)^2\)只有一個交點，但此時二者是相交的，不是相切的。

8、當直線和曲線只有一個交點，不能說二者相切，有可能相交(如上)；當直線和曲線有不止一個交點時，不能說二者不相切，有可能其中某一個交點就是切點；

9、函數的導數是個常數，記作\(f'(x_0)\)或者\(y'|_{x=x_0}\)；而導函數是個函數，是個變量，記作\(f'(x)\)或\(y'|_{x}\)，
如已知函數\(f(x)=x^2+2f'(2)x+3\)，求函數的解析式就是利用函數的導數是個常數，給函數求導得到，\(f'(x)=2x+2f'(2)\)，令\(x=2\)，解得\(f'(2)=-4\)，故函數的解析式為\(f(x)=x^2-8x+3\)。

10、實際問題中的導數的意義：

在不同的實際問題中，導數的意義是不相同的。比如：功率是功關於時間的導數；速度是路程關於時間的導數；加速度是速度關於時間的導數；線密度是質量關於長度的導數；邊際成本是成本關於產量的導數；氣球的膨脹率是氣球半徑關於體積的導數。

函數的導數概念