數學概念理解 - 梯度與方向導數
阿新 • • 發佈:2019-01-06
一.梯度
- 定義:設函式
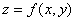 在平面區域
在平面區域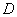 內具有一階連續偏導數,則對於每一點
內具有一階連續偏導數,則對於每一點
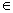
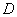 ,都可定出一個向量
,都可定出一個向量
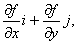
這向量稱為函式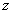 =
= 在點
在點
 的梯度,記作
的梯度,記作

 ,即
,即


 =
= 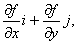
- 性質:梯度的方向是函式值增大最快的方向。相應的,負梯度的方向是函式值減小最快的方向。=> 梯度下降法求函式最值。
二.方向導數
- 定義:設函式
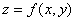 在點
在點
 的某一鄰域
的某一鄰域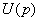 內有定義.自點
內有定義.自點 引射線
引射線 .設
.設 軸正向到射線
軸正向到射線 的轉角為
的轉角為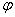 (逆時針方向:
(逆時針方向: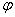
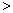 0;順時針方向:
0;順時針方向: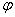
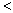 0),並設
0),並設 '(
'( +△
+△ ,
,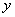 +△
+△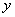 )為
)為 上的另一點且
上的另一點且 '∈
'∈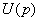 .我們考慮函式的增量
.我們考慮函式的增量 (
( +△
+△ ,
,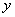 +△
+△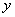 )-
)-
 與
與 、
、 '兩點間的距離
'兩點間的距離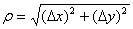 的比值.當
的比值.當 '沿著
'沿著 趨於
趨於 時,如果這個比的極限存在,則稱這極限為函式
時,如果這個比的極限存在,則稱這極限為函式
 在點
在點 沿方向
沿方向 的方向導數,記作
的方向導數,記作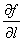 ,即
,即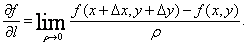 (1)
(1)
從定義可知,當函式
 在點
在點
 的偏導數
的偏導數 x、
x、 y存在時,函式在點
y存在時,函式在點 沿著
沿著 軸正向
軸正向
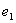 =
=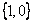 ,
,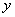 軸正向
軸正向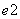 =
=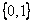 的方向導數存在且其值依次為
的方向導數存在且其值依次為 x、
x、 y,函式
y,函式
 在點
在點 沿
沿 軸負向
軸負向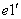 =
=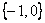 ,
,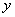 軸負向
軸負向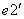 =
=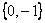 的方向導數也存在且其值依次為-
的方向導數也存在且其值依次為- x、-
x、- y.
y. - 定理 如果函式
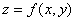 在點
在點
 是可微分的,那末函式在該點沿任一方向的方向導數都存在,且有
是可微分的,那末函式在該點沿任一方向的方向導數都存在,且有
![]()
![]() (2)
(2)
其中![]() 為
為![]() 軸到方向
軸到方向![]() 的轉角.
的轉角.
