題目大意

對於撲克牌的一次洗牌是這樣定義的，將一疊N（N為偶數）張撲克牌平均分成上下兩疊，取下面一疊的第一張作為新的一疊的第一張，然後取上面一疊的第一張作為新的一疊的第二張，再取下面一疊的第二張作為新的一疊的第三張……如此交替直到所有的牌取完。

如果對一疊6張的撲克牌1 2 3 4 5 6，進行一次洗牌的過程如下圖所示：

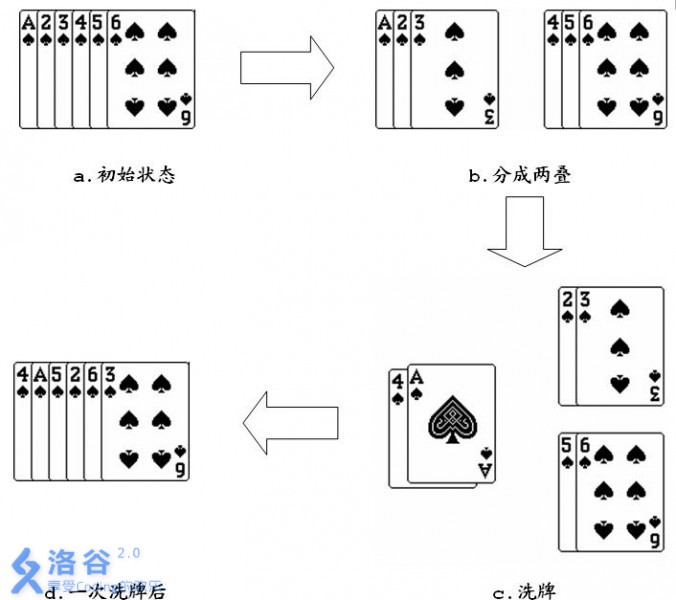
如果給定長度為N的一疊撲克牌，並且牌面大小從1開始連續增加到N（不考慮花色），對這樣的一疊撲克牌，進行M次洗牌。說出經過洗牌後的撲克牌序列中第L張撲克牌的牌面大小是多少。

思路

我們看看一張位於位置p撲克牌洗一次後的位置p‘在哪裏。若p<=N/2，這張撲克牌就到了第p對牌中的第2張，位置為p*2；若p>N/2，這張撲克牌就到了第p-N/2對牌中的第一張，故p‘=(p-N/2)*2-1=p*2-(N+1)。因為p<=N/2時p*2%(N+1)=p*2，所以綜上所述，p‘=p*2%(N+1)。洗m次，即令運算*2%(N+1)進行m次，2便乘了m次，模了m遍N+1與只模一次的效果是相同的。綜上所述，洗m次後牌移動到了位置p*2^m%(N+1)。現在給出最終的位置l，那麽就是讓我們解同余方程x*2^m≡l(mod N+1)。利用快速冪求2^m，然後解方程模板代入即可。

#include <cstdio>
#include <cstring>
using namespace std;

#define ll long long

ll Mult(ll a, ll b, ll p)
{
	ll ans = 0;
	while (b)
	{
		if (b & 1)
			ans = (ans + a) % p;
		a = (a+a)%p;
		b >>= 1;
	}
	return ans;
}

ll Power(ll a, ll n, ll p)
{
	ll ans = 1;
	while (n)
	{
		if (n & 1)
			ans = Mult(ans, a, p);
		a = Mult(a, a, p);
		n >>= 1;
	}
	return ans;
}

ll Exgcd(ll a, ll b, ll &x, ll &y)
{
	if (b == 0)
	{
		x = 1;
		y = 0;
		return a;
	}
	ll d = Exgcd(b, a%b, x, y);
	ll tx = x;
	x = y;
	y = tx - (a / b) * y;
	return d;
}

ll Gcd(ll a, ll b)
{
	return b ? Gcd(b, a%b) : a;
}

ll Eq(ll a, ll b, ll m)
{
	ll gcd = Gcd(a, m);
	if (b%gcd)
		return -1;
	ll x, y;
	Exgcd(a, m, x, y);
	x = x * b / gcd;
	ll p = m / gcd;
	return (x%p+p) % p;
}

int main()
{
#ifdef _DEBUG
	freopen("c:\\noi\\source\\input.txt", "r", stdin);
#endif
	ll n, m, l;
	scanf("%lld%lld%lld", &n, &m, &l);
	printf("%lld\n", Eq(Power(2, m, n + 1), l, n+1));
	return 0;
}

luogu2054 洗牌 同余方程