題目大意

Mayan puzzle是最近流行起來的一個遊戲。遊戲界面是一個77 行\times 5×5列的棋盤，上面堆放著一些方塊，方塊不能懸空堆放，即方塊必須放在最下面一行，或者放在其他方塊之上。遊戲通關是指在規定的步數內消除所有的方塊，消除方塊的規則如下：

1 、每步移動可以且僅可以沿橫向（即向左或向右）拖動某一方塊一格：當拖動這一方塊時，如果拖動後到達的位置（以下稱目標位置）也有方塊，那麽這兩個方塊將交換位置（參見輸入輸出樣例說明中的圖66到圖77 ）；如果目標位置上沒有方塊，那麽被拖動的方塊將從原來的豎列中抽出，並從目標位置上掉落（直到不懸空，參見下面圖1 和圖2）；

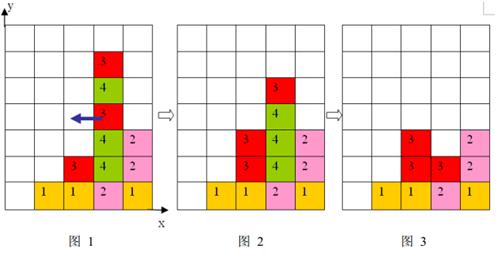
2 、任一時刻，如果在一橫行或者豎列上有連續三個或者三個以上相同顏色的方塊，則它們將立即被消除（參見圖1 到圖3）。

註意：

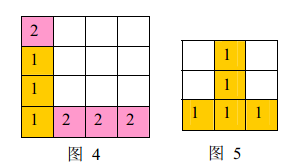
a) 如果同時有多組方塊滿足消除條件，幾組方塊會同時被消除（例如下面圖44 ，三個顏色為11 的方塊和三個顏色為 22 的方塊會同時被消除，最後剩下一個顏色為22的方塊）。

b) 當出現行和列都滿足消除條件且行列共享某個方塊時，行和列上滿足消除條件的所有方塊會被同時消除（例如下面圖5 所示的情形，5 個方塊會同時被消除）。

3 、方塊消除之後，消除位置之上的方塊將掉落，掉落後可能會引起新的方塊消除。註意：掉落的過程中將不會有方塊的消除。

上面圖1 到圖 3 給出了在棋盤上移動一塊方塊之後棋盤的變化。棋盤的左下角方塊的坐標為（0, 0 ），將位於（3, 3 ）的方塊向左移動之後，遊戲界面從圖 1 變成圖 2 所示的狀態，此時在一豎列上有連續三塊顏色為4 的方塊，滿足消除條件，消除連續3 塊顏色為4 的方塊後，上方的顏色為3 的方塊掉落，形成圖 3 所示的局面。

若有解，輸出具體移動方案，否則輸出-1.

題解

如何模擬消除過程

1. 每當我們消除掉一組塊後，剩余的塊新的排列方式我們是不可預估的。所以，我們應當不斷對全局進行可消除的塊的搜索並消除，而不是刪除哪個塊就在哪個塊附近嘗試考慮各種情況來刪除。
2. 對於一組塊如何刪除？一定不要忘記圖5的情況！另外，在時間復雜度夠的情況下，我們要盡可能使用簡單粗暴的形式解決問題。與其邊刪塊邊讓上面的塊下落，不如刪的時候只刪不下落，最後設置個DropAll函數把所有塊整體下落，這樣一定不會錯。

如何剪枝

1. 優化搜索順序：根據題目中的優先級，我們可以按從左到右、從下至上進行搜索。
2. 排除等效冗余：我們不允許兩個顏色相同的塊交換；所有塊不可以與左側相鄰的塊交換。
3. 可行性剪枝：本題看不出什麽規律來，無法在此處剪枝。
4. 最優性剪枝：本題沒要你求最優解，無法在此處剪枝。
5. 記憶化：本題狀態存儲不了，無法在此處剪枝。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cassert>
using namespace std;

const int MAX_ROW = 10, MAX_COL = 10;
const int TotX = 5, TotY = 7;
int N;

struct Matrix
{
	int A[MAX_ROW][MAX_COL];

private:
	int GetHorSum(int x, int y)
	{
		int color = A[x][y];
		int ans = 1;
		for (int i = x - 1; i >= 0 && A[i][y] == color; i--)
			ans++;
		for (int i = x + 1; i < TotX && A[i][y] == color; i++)
			ans++;
		return ans;
	}

	int GetVerSum(int x, int y)
	{
		int color = A[x][y];
		int ans = 1;
		for (int i = y + 1; i < TotY && A[x][i] == color; i++)
			ans++;
		for (int i = y - 1; i >= 0 && A[x][i] == color; i--)
			ans++;
		return ans;
	}

	void DropOne(int x, int y)
	{
		if (A[x][y])
			for (int i = y - 1; i >= 0 && !A[x][i]; i--)
				swap(A[x][i], A[x][i + 1]);
	}

	void DropAll()
	{
		for (int x = 0; x < TotX; x++)
			for (int y = 0; y < TotY; y++)
				DropOne(x, y);
	}

	void RemoveHor(int, int);
	void RemoveVer(int, int);

	bool Remove(int x, int y)
	{
		if (GetHorSum(x, y) >= 3)
		{
			RemoveHor(x, y);
			DropAll();
			return true;
		}
		if (GetVerSum(x, y) >= 3)
		{
			RemoveVer(x, y);
			DropAll();
			return true;
		}
		return false;
	}

	bool Search_Remove()
	{
		for (int x = 0; x < TotX; x++)
			for (int y = 0; y < TotY && A[x][y]; y++)
				if (Remove(x, y))
					return true;
		return false;
	}

	void RemoveAll()
	{
		while (Search_Remove());
	}

public:
	Matrix operator = (const Matrix& a)
	{
		memcpy(A, a.A, sizeof(a.A));
		return *this;
	}

	bool operator == (const Matrix& a) const
	{
		return !memcmp(A, a.A, sizeof(A));
	}

	bool Empty()
	{
		for (int x = 0; x < TotX; x++)
			if (A[x][0])
				return false;
		return true;
	}

	Matrix Move(int x, int y, int dir)
	{
		Matrix ans;
		ans = *this;
		assert(ans.A[x][y]);
		assert(x + dir < TotX && x + dir >= 0);
		if (ans.A[x + dir][y])
			swap(ans.A[x][y], ans.A[x + dir][y]);
		else
		{
			swap(ans.A[x][y], ans.A[x + dir][y]);
			ans.DropAll();
		}
		ans.RemoveAll();
		return ans;
	}
};

void Matrix::RemoveHor(int x, int y)
{
	int color = A[x][y];
	A[x][y] = 0;
	for (int i = x - 1; i >= 0 && A[i][y] == color; i--)
	{
		if (GetVerSum(i, y) >= 3)
			RemoveVer(i, y);
		A[i][y] = 0;
	}
	for (int i = x + 1; i < TotX && A[i][y] == color; i++)
	{
		if (GetVerSum(i, y) >= 3)
			RemoveVer(i, y);
		A[i][y] = 0;
	}
}

void Matrix::RemoveVer(int x, int y)
{
	int color = A[x][y];
	A[x][y] = 0;
	for (int i = y - 1; y >= 0 && A[x][i] == color; i--)
	{
		if (GetHorSum(x, i) >= 3)
			RemoveHor(x, i);
		A[x][i] = 0;
	}
	for (int i = y + 1; y < TotY && A[x][i] == color; i++)
	{
		if (GetHorSum(x, i) >= 3)
			RemoveHor(x, i);
		A[x][i] = 0;
	}
}


struct State
{
	Matrix mat;
	int X, Y, Dir;
}States[10];

bool Ok(int cnt)
{
	for (int i = 0; i < cnt; i++)
		if (States[i].mat == States[cnt].mat)
			return false;
	return true;
}

int Dfs(int cnt)
{
	if (cnt > N)
		return -1;
	for (int x = 0; x < TotX; x++)
		for (int y = 0; y < TotY && States[cnt - 1].mat.A[x][y]; y++)
		{
			States[cnt].X = x;
			States[cnt].Y = y;
			const Matrix& matFrom = States[cnt - 1].mat;
			if (x <= TotX - 2 && matFrom.A[x + 1][y] != matFrom.A[x][y])
			{
				States[cnt].Dir = 1;
				States[cnt].mat = States[cnt - 1].mat.Move(x, y, 1);
				if (States[cnt].mat.Empty())
					return cnt;
				if (Ok(cnt))
				{
					int nextAns = Dfs(cnt + 1);
					if (nextAns > -1)
						return nextAns;
				}
			}
			if (x >= 1 && !matFrom.A[x - 1][y])
			{
				States[cnt].Dir = -1;
				States[cnt].mat = States[cnt - 1].mat.Move(x, y, -1);
				if (States[cnt].mat.Empty())
					return cnt;
				if (Ok(cnt))
				{
					int nextAns = Dfs(cnt + 1);
					if (nextAns > -1)
						return nextAns;
				}
			}
		}
	return -1;
}

int main()
{
	scanf("%d", &N);
	for (int x = 0; x < TotX; x++)
		for (int y = 0; scanf("%d", &States[0].mat.A[x][y]) && States[0].mat.A[x][y]; y++);

	int cnt = Dfs(1);
	if (cnt == -1)
		printf("-1\n");
	else
	{
		for (int i = 1; i <= cnt; i++)
			printf("%d %d %d\n", States[i].X, States[i].Y, States[i].Dir);
	}
	return 0;
}

luogu1312 Mayan遊戲 剪枝