題面

題目描述
$ Mayan puzzle $是最近流行起來的一個遊戲。遊戲介面是一個 \(7行 \times 5列\)的棋盤，上面堆放著一些方塊，方塊不能懸空堆放，即方塊必須放在最下面一行，或者放在其他方塊之上。遊戲通關是指在規定的步數內消除所有的方塊，消除方塊的規則如下：

1 、每步移動可以且僅可以沿橫向（即向左或向右）拖動某一方塊一格：當拖動這一方塊時，如果拖動後到達的位置（以下稱目標位置）也有方塊，那麼這兩個方塊將交換位置（參見輸入輸出樣例說明中的圖\(6\)到圖\(7\)）；如果目標位置上沒有方塊，那麼被拖動的方塊將從原來的豎列中抽出，並從目標位置上掉落（直到不懸空，參見下面圖1 和圖2）；

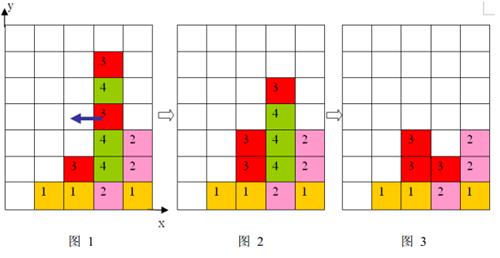
2 、任一時刻，如果在一橫行或者豎列上有連續三個或者三個以上相同顏色的方塊，則它們將立即被消除（參見圖1 到圖3）。

注意：

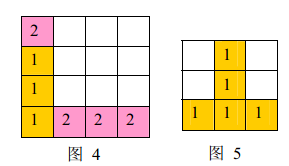
a) 如果同時有多組方塊滿足消除條件，幾組方塊會同時被消除（例如下面圖\(4\)，三個顏色為\(1\)的方塊和三個顏色為$2 $的方塊會同時被消除，最後剩下一個顏色為\(2\)的方塊）。

b) 當出現行和列都滿足消除條件且行列共享某個方塊時，行和列上滿足消除條件的所有方塊會被同時消除（例如下面圖5 所示的情形，5 個方塊會同時被消除）。

3 、方塊消除之後，消除位置之上的方塊將掉落，掉落後可能會引起新的方塊消除。注意：掉落的過程中將不會有方塊的消除。

上面圖1 到圖 3 給出了在棋盤上移動一塊方塊之後棋盤的變化。棋盤的左下角方塊的座標為（0, 0 ），將位於（3, 3 ）的方塊向左移動之後，遊戲介面從圖 1 變成圖 2 所示的狀態，此時在一豎列上有連續三塊顏色為4 的方塊，滿足消除條件，消除連續3 塊顏色為4 的方塊後，上方的顏色為3 的方塊掉落，形成圖 3 所示的局面。

輸入輸出格式
輸入格式：
共 6 行。

第一行為一個正整數\(n\)，表示要求遊戲通關的步數。

接下來的\(5\)行，描述$ 7 \times 5$的遊戲介面。每行若干個整數，每兩個整數之間用一個空格隔開，每行以一個$0 $結束，自下向上表示每豎列方塊的顏色編號（顏色不多於\(10\)

輸入資料保證初始棋盤中沒有可以消除的方塊。

輸出格式：
如果有解決方案，輸出\(n\)行，每行包含\(3\)個整數\(x,y,g\)，表示一次移動，每兩個整數之間用一個空格隔開，其中\((x,y)\)表示要移動的方塊的座標，\(g\)表示移動的方向，\(1\)表示向右移動，\(−1\)表示向左移動。注意：多組解時，按照xx為第一關健字，\(y\)為第二關健字，\(1\)優先於\(−1\)，給出一組字典序最小的解。遊戲介面左下角的座標為\((0,0)\)。

如果沒有解決方案，輸出一行，包含一個整數\(-1\)。

輸入輸出樣例
輸入樣例#1：
3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0
輸出樣例#1：
2 1 1
3 1 1
3 0 1

說明
【輸入輸出樣例說明】
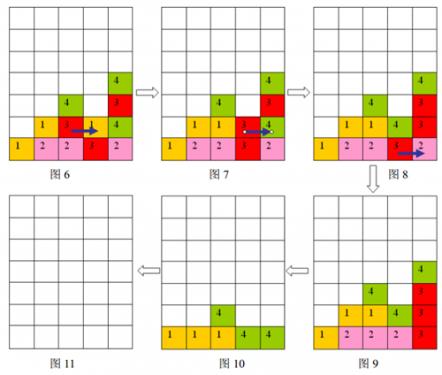
按箭頭方向的順序分別為圖\(6\)到圖\(11\)
樣例輸入的遊戲局面如上面第一個圖片所示，依次移動的三步是：\((2,1)\)處的方格向右移動，\((3,1)\)處的方格向右移動，\((3,0)\)處的方格向右移動，最後可以將棋盤上所有方塊消除。

【資料範圍】
對於\(30%\)的資料，初始棋盤上的方塊都在棋盤的最下面一行；
對於\(100%\)的資料，\(0<n≤5\) 。

思路

覺得這道題寫得挺有意思的，思路有空再補吧233，程式碼也沒註釋……

程式碼

#include<iostream>
#include<cstdio>
#include<cstdlib>
#define re register
using namespace std;
//全域性變數
int n;//步數
int step[10][10][10];//dfs狀態回溯 
struct result_ans {
    int x,y,way;
}ans[10];//答案儲存 
// Mayan遊戲實現部分 
struct Mayan_puzzle {
    int a[10][10];//color <=10
    int ax[105],ay[105],T;
    inline bool go() {    //遊戲進行-判斷是否可以消除並消除 
        T=0;    int flag=0;
        for(re int i=0;i<=2;i++)
            for(re int j=0;j<=6;j++) if(a[i][j]) {
            if(a[i][j]==a[i+1][j]&&a[i+1][j]==a[i+2][j]) {
                flag = 1; ax[++T] = i; ay[T] = j;
                ax[++T]=i+1; ay[T]=j; ax[++T]=i+2; ay[T]=j;
            }
        }
        for(re int i=0;i<=4;i++)
            for(re int j=0;j<=4;j++) if(a[i][j]) {
            if(a[i][j]==a[i][j+1]&&a[i][j+1]==a[i][j+2]) {
                flag = 1; ax[++T] = i; ay[T] = j;
                ax[++T]=i; ay[T]=j+1; ax[++T]=i; ay[T]=j+2;
            }
        }   
        for(re int i=1;i<=T;i++) a[ax[i]][ay[i]]=0;
        return flag;
    }
    inline void down() {    //下降處理-懸空方塊下落 
        for(re int i=0;i<=4;i++)
            for(re int j=1;j<=6;j++) if(a[i][j])    {
            int k=j;
            while(a[i][k-1]==0) {
                swap(a[i][k-1],a[i][k]);
                if(k==1) break; else k--;
            }
        }
    }
    inline bool check() {   //結束判斷-判斷是否全部消除 
        for(re int i=0;i<=4;i++)
            if(a[i][0]) return false;
        return true;
    }
};
struct Mayan_puzzle p;
// in / out 輸入輸出 
inline void getin() {
    int color=0,T;  scanf("%d",&n);
    for(re int i=0;i<=4;i++) {  T=-1;
        while(scanf("%d",&color)&&color) p.a[i][++T]=color;
    }
}
inline void print() {
    for(re int i=1;i<=n;i++)
        printf("%d %d %d\n",ans[i].x,ans[i].y,ans[i].way);
}
// dfs 搜尋部分 
void dfs(int cur) {
    if(cur>n) {
        if(p.check()) {
            print();//out
            exit(0);//退出程式 
        }
        return;
    }
    for(re int i=0;i<=4;i++)
        for(re int j=0;j<=6;j++)
    {   
        if(p.a[i][j]&&i<=3) {   //right
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    step[cur][k][l] = p.a[k][l];
            swap( p.a[i][j] , p.a[i+1][j] );
            ans[cur].x =i; ans[cur].y =j; ans[cur].way =1;
            p.down();
            while( p.go())  p.down();
            dfs(cur+1);
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    p.a[k][l] = step[cur][k][l];
        }
        if(p.a[i][j]&&p.a[i-1][j]==0&&i>=1) {   //left
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    step[cur][k][l] = p.a[k][l];
            swap( p.a[i][j] , p.a[i-1][j] );
            ans[cur].x =i; ans[cur].y =j; ans[cur].way =-1;
            p.down();
            while( p.go())  p.down();
            dfs(cur+1);
            for(re int k=0;k<=4;k++)
                for(re int l=0;l<=6;l++)
                    p.a[k][l] = step[cur][k][l];
        }
    }
}
//main函式 
int main() {
    getin();//in
    dfs(1);//dfs
    printf("-1\n");//無解時輸出-1 
    return 0;
}