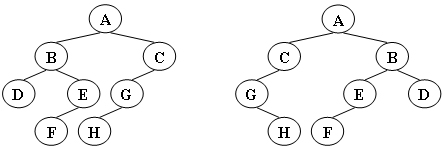
03-樹1 樹的同構 （25 分）

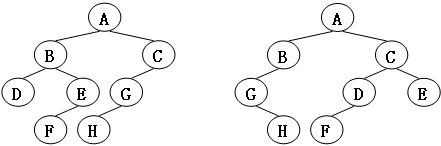
給定兩棵樹T1和T2。如果T1可以通過若幹次左右孩子互換就變成T2，則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的，因為我們把其中一棵樹的結點A、B、G的左右孩子互換後，就得到另外一棵樹。而圖2就不是同構的。

圖1

圖2

輸入格式:

輸入給出2棵二叉樹樹的信息。對於每棵樹，首先在一行中給出一個非負整數N (≤10)，即該樹的結點數（此時假設結點從0到N?1編號）；隨後N行，第i行對應編號第i個結點，給出該結點中存儲的1個英文大寫字母、其左孩子結點的編號、右孩子結點的編號。如果孩子結點為空，則在相應位置上給出“-”。給出的數據間用一個空格分隔。註意：題目保證每個結點中存儲的字母是不同的。

輸出格式:

如果兩棵樹是同構的，輸出“Yes”，否則輸出“No”。

輸入樣例1（對應圖1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

輸出樣例1:

Yes

輸入樣例2（對應圖2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

輸出樣例2:

No

using System;
using
 
 System.Collections.Generic;
using System.Threading;
using System.Threading.Tasks;
using System.Diagnostics;
using System.Net;
using System.Text;
using System.Xml;

struct Point
{
    public string C;
    public string X;
    public string Y;
    public Point(string v1, string v2, string v3) : this()
    {
        
 
this.C = v1;
        this.X = v2;
        this.Y = v3;
    }
}

class P
{


    public XmlDocument doc = new XmlDocument();
    public P(string v2) : this(int.Parse(v2))
    {

    }
    List<Point> tempList = new List<Point>();
    public P(int v1)
    {
        if (v1 > 0)
        {
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < v1; i++)
            {
                var temp = Console.ReadLine().Split(new[] { " " }, StringSplitOptions.RemoveEmptyEntries);

                tempList.Add(new Point(temp[0], temp[1], temp[2]));
                sb.Append(temp[1]);
                sb.Append(temp[2]);
            }
            var item = new Point();
            string sss = sb.ToString();
            for (int i = 0; i < v1; i++)
            {
                if (!sss.Contains(i + ""))
                {
                    item = tempList[i];
                }
            }



            var xNode = doc.CreateNode(XmlNodeType.Element, "item", "");

            var attr1 = doc.CreateAttribute("x");
            attr1.Value = item.X;
            var attr2 = doc.CreateAttribute("y");
            attr2.Value = item.Y;
            var attr3 = doc.CreateAttribute("n");
            attr3.Value = item.C;

            xNode.Attributes.Append(attr1);
            xNode.Attributes.Append(attr2);
            xNode.Attributes.Append(attr3);
            GetNodes(xNode);

            doc.AppendChild(xNode);

        }
    }

    private void GetNodes(XmlNode xNode)
    {
        int x = -1;
        int y = -1;
        if (int.TryParse(xNode.Attributes["x"].Value, out x))
        {

            var item = tempList[x];

            var node = doc.CreateNode(XmlNodeType.Element, "item", "");
            var attr1 = doc.CreateAttribute("x");
            attr1.Value = item.X;
            var attr2 = doc.CreateAttribute("y");
            attr2.Value = item.Y;
            var attr3 = doc.CreateAttribute("n");
            attr3.Value = item.C;

            node.Attributes.Append(attr1);
            node.Attributes.Append(attr2);
            node.Attributes.Append(attr3);
            GetNodes(node);

            xNode.AppendChild(node);
        }
        if (int.TryParse(xNode.Attributes["y"].Value, out y))
        {

            var item = tempList[y];

            var node = doc.CreateNode(XmlNodeType.Element, "item", "");
            var attr1 = doc.CreateAttribute("x");
            attr1.Value = item.X;
            var attr2 = doc.CreateAttribute("y");
            attr2.Value = item.Y;
            var attr3 = doc.CreateAttribute("n");
            attr3.Value = item.C;

            node.Attributes.Append(attr1);
            node.Attributes.Append(attr2);
            node.Attributes.Append(attr3);
            GetNodes(node);

            xNode.AppendChild(node);
        }
    }
}

class T
{


    static bool 對比(XmlNode p1, XmlNode p2)
    {   if (p1.Attributes["n"] .Value== p2.Attributes["n"].Value)
        {

            if (p1.ChildNodes.Count == 0 &&
                        p2.ChildNodes.Count == 0)
            {

                return true;
            }
            if (p1.ChildNodes.Count == 1 &&
                p2.ChildNodes.Count == 1)
            {
                return 對比(p1.ChildNodes[0], p2.ChildNodes[0]);
            }
            if (p1.ChildNodes.Count == 2 &&
                      p2.ChildNodes.Count == 2)
            {
                var b00 = 對比(p1.ChildNodes[0], p2.ChildNodes[0]);
                var b11 = 對比(p1.ChildNodes[1], p2.ChildNodes[1]);
                var b10 = 對比(p1.ChildNodes[1], p2.ChildNodes[0]);
                var b01 = 對比(p1.ChildNodes[0], p2.ChildNodes[1]);
                return (b00 && b11) || (b10 && b01);
            }
        }
        return false;
    }
    static void Main(string[] args)
    {
        P p1 = new P(Console.ReadLine());
        P p2 = new P(Console.ReadLine());
        
        
        if (p1.doc.ChildNodes.Count == 0 &&
            p2.doc.ChildNodes.Count == 0)
        {
            Console.WriteLine("Yes");
            return;
        }
        else
        {
            bool b = 對比(p1.doc.ChildNodes[0], p2.doc.ChildNodes[0]);


            if (b)
                Console.WriteLine("Yes");
            else
                Console.WriteLine("No");
        }
    }


}

03-樹1 樹的同構 （25 分）