統計學(二)之一般線性模型(三)
阿新 • • 發佈:2018-10-31
多因素方差分析

與單因素方差分析不同的是,多個處理的自變數。

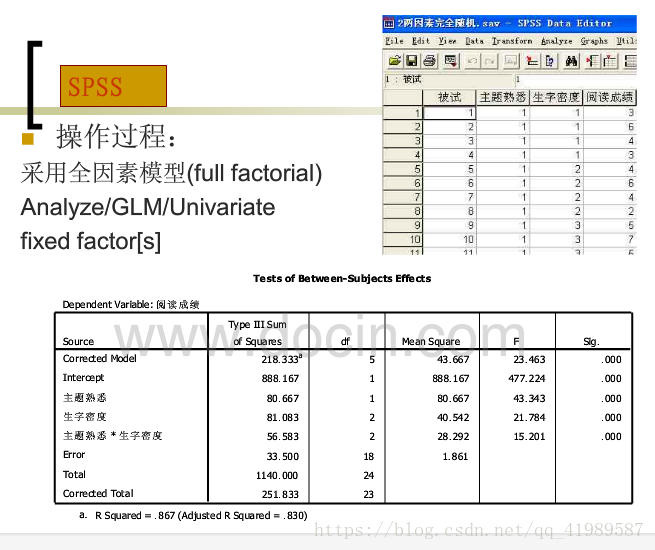
表中第四行第五行都是主效應,第六行是互動效應。
對互動作用的進一步檢驗
當方差分析發現一個兩次互動作用時,需要進一步檢驗,以說明兩個因素之間互動作用的實質。
方法一:互動作用的圖解
一般線性模型-繪製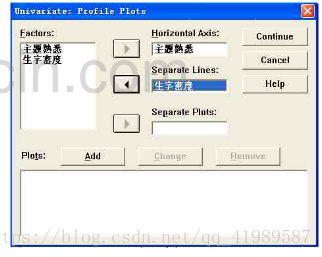
相互平行的線——無互動效應
不平行的線——存在互動效應
方法二:簡單效應(在一般線性模型(一)裡面講過)
例如在一個2*2兩因素實驗中,A因素和B因素各有兩個水平。A因素的兩個水平在B1水平的方差叫A在B1水平的簡單效應,A因素的兩個水平在B2水平的方差叫A在B2水平的簡單效應。同樣的,對B也是一樣。
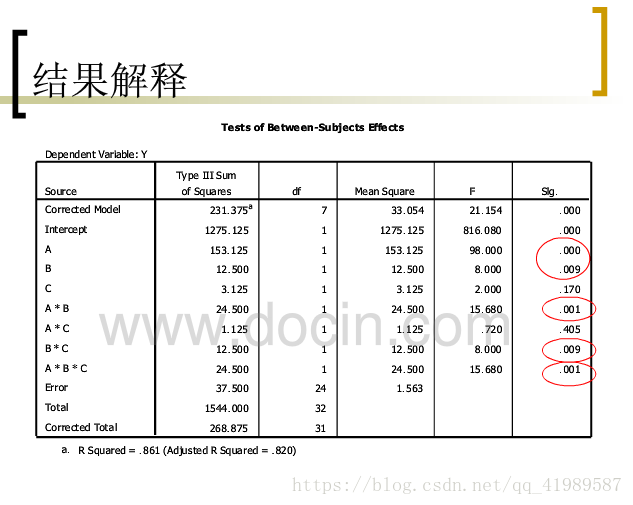
重複測量方差分析
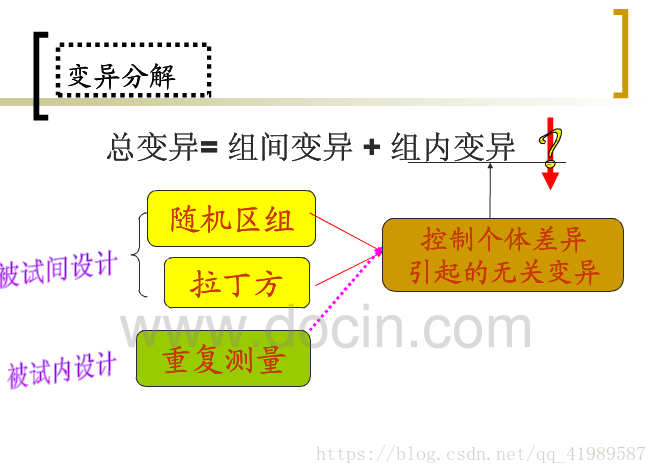
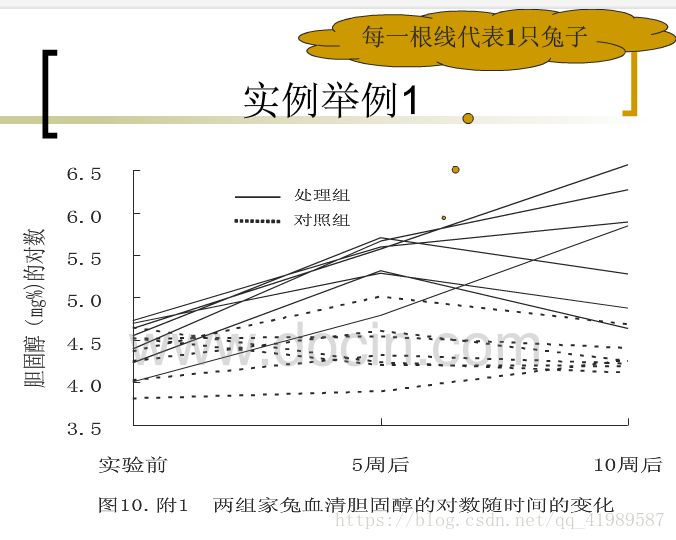
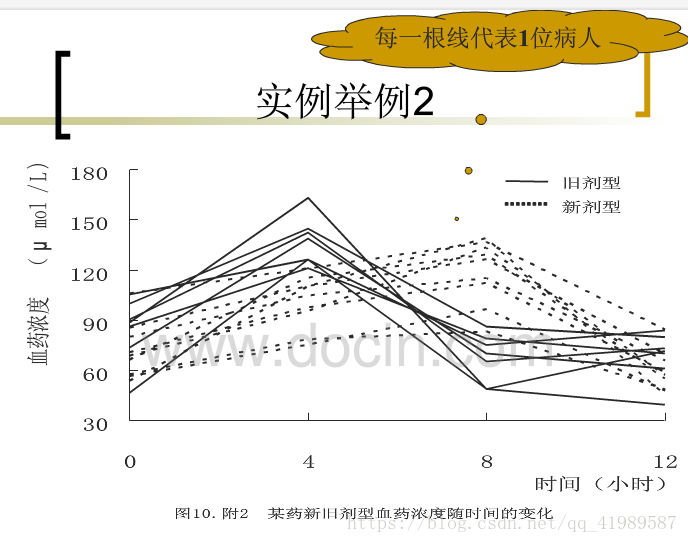
重複測量是指對同一研究物件的某一觀察指標在不同場合進行的多次測量。
被試間設計:每個被試接受一個處理水平,被試的個體差異帶來的變異混雜在誤差變異中。
被試內設計(重複測量):每個被試接受所有的處理水平。但是進行被試內處理的一個前提假設是被試接受前面的處理對接受後面的處理沒有長期影響。
重複測量資料的方差分析對協方陣的要求
- 樣本是隨機的;
- 在處理因素的同一水平上的測定值都來自正態總體;
- 每一水平上的測定值都來自正態總體;
- 各時間點組成的協方差陣具有球形性特徵;
Box指出,若球形性質得不到滿足,則方差分析的F值是有偏的,這會造成過多的拒絕本來是真的無效假設(即增加了|型錯誤)。
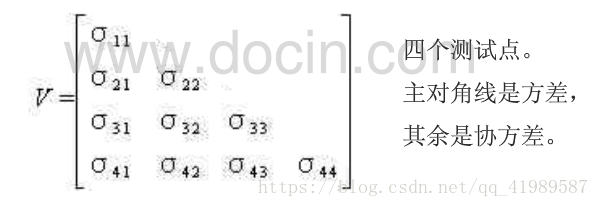
協方差陣
方差是指在某一時間點上測量值變異性的大小,而協方差是指在兩個不同時間點上測量值相互變異性的大小。如果在某個時間點上的取值不影響其他時間點上的取值,則協方差為0,反之,則不為0.由協方差構成的矩陣稱為協方差陣。
未完待續。。。。。。