OpenGL ES 正交投影
OpenGL ES 正交投影
繪製正方形
在最開始繪製的六邊形裡面好像看起來挺容易的,也沒有出現什麼問題,接下來不妨忘記前面繪製六邊形的程式碼,讓我們按照自己的理解來繪製一個簡單的正方形。
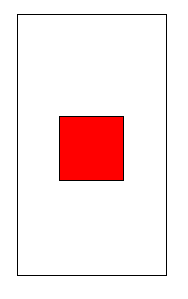
按照我的理解,要想在螢幕中間顯示一個正方形,效果如下圖所示
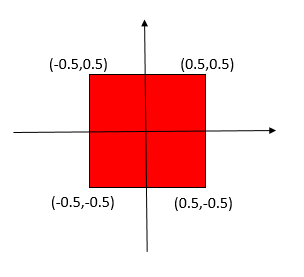
應該建立的資料如下圖所示
即傳給渲染管線的頂點資料如下圖:
float 於是程式碼大概是這樣子的,這裡省略掉與主題無關的程式碼,顏色用純色填充,因此在片元著色器中指定顏色,也省略掉一系列矩陣變換。頂點著色器中直接將頂點傳給渲染管線,片元著色器中給片元設定固定顏色紅色。
Rectangle.java
public class Rectangle {
private FloatBuffer mVertexBuffer;
private int mProgram;
private int mPositionHandle;
public Rectangle(float r) {
initVetexData(r);
}
public void initVetexData(float r) {
// 初始化頂點座標
float[] vertexArray = new float[] {
(float RectangleView.java
public class RectangleView extends GLSurfaceView{
public RectangleView(Context context) {
super(context);
setEGLContextClientVersion(2);
setRenderer(new MyRender());
}
class MyRender implements GLSurfaceView.Renderer {
private Rectangle rectangle;
@Override
public void onSurfaceCreated(GL10 gl, EGLConfig config) {
GLES20.glClearColor(0.5f, 0.5f, 0.5f, 1);
rectangle = new Rectangle(0.5f);
GLES20.glEnable(GLES20.GL_DEPTH_TEST);
}
@Override
public void onSurfaceChanged(GL10 gl, int width, int height) {
GLES20.glViewport(0, 0, width, height);
}
@Override
public void onDrawFrame(GL10 gl) {
GLES20.glClear( GLES20.GL_DEPTH_BUFFER_BIT | GLES20.GL_COLOR_BUFFER_BIT);
rectangle.draw();
}
}
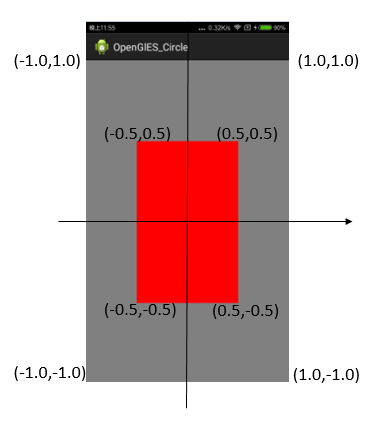
}然後出來的效果是這樣子的,實際上螢幕上的座標並不是這樣子的,後面可以知道上面畫的這個樣子其實只是一個歸一化的裝置座標。歸一化裝置座標可以通過公式對映到實際的手機螢幕,後面會學到。
咦,實際效果好像和想象中的不太一樣呀。我的本意是顯示一個正方形,但實際上現實的卻是一個矩形了,y軸上被拉伸了,並且橫屏狀態下也是類似的情況。但比較巧的是,如果以螢幕中心做一個座標軸,就會發現,這個矩形的四個頂點在這個座標軸x、y範圍為[-1,1]的中間。
實際上,要顯示的所有物體對映到手機螢幕上,都是要對映到x、y、z軸上的[-1,1]範圍內,這個範圍內的座標稱為歸一化裝置座標,獨立於螢幕的實際尺寸和形狀。
因此按照這樣的規定,我們要建立一個正方形就非常困難了,因為要建立正方形就必須考慮手機的寬高比,傳入資料的時候就比較複雜了:不能僅僅站在要繪製物體的自身角度來看了。也就是說,上面的例子中要繪製一個正方形,傳入的頂點資料的y座標要按照比例進行一點轉換,比如對16:9的螢幕,將上面傳入的頂點資料的y座標都乘以9/16即可。但同時會發現當處於橫屏時,又要處理傳入的x座標的值,顯然這不是一個好的方案。
引入投影
實際上,對於一個物體來說它有它自身的座標,這個空間稱為物體空間,也就是設計物體的時候採用的一個座標空間,物體的幾何中心在座標原點上,歸一化後坐標範圍在[-1,1]之間,x和y軸分度是一致的。
將在這個空間的物體直接往手機螢幕的歸一化座標繪製時,由於螢幕的寬高比的問題,就會出現和預料結果不一樣。所以只需要對物體空間的座標做一個對映即可。
正交投影就是為了解決這個問題的,
public static void orthoM(float[] m, int mOffset,
float left, float right, float bottom, float top,
float near, float far)正交投影背後的數學
orthoM函式產生的矩陣會把所有的左右之間、上下之間,遠近之間的點對映到歸一化裝置座標中。
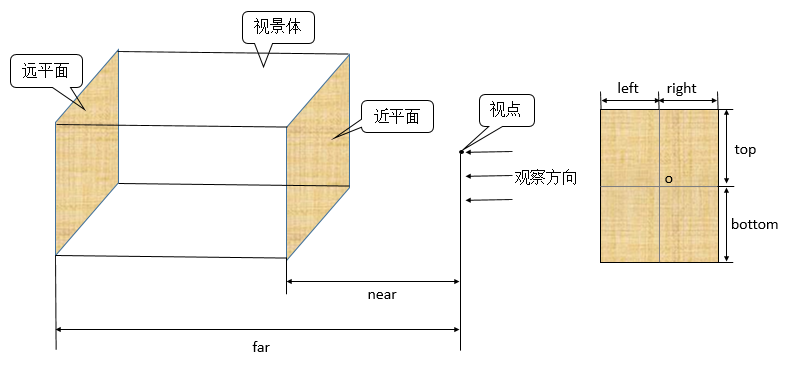
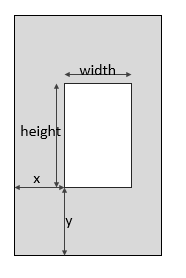
各引數的含義如圖所示
正交投影是一種平行投影,投影線是平行的,其視景體是一個長方體,座標位於視景體中的物體才有效,視景體裡面的物體投影到近平面上的部分最終會顯示到螢幕的視口中,關於視口後面會降到。
會產生下面的矩陣,z軸的負值會反轉z座標,這是因為歸一化裝置座標是左手系統,而OpenGL ES中的座標系統都是右手系統,這裡還涉及到頂點座標的w分量,目前暫時用不到。
利用矩陣的就可以將物體空間[-1,1]之間的座標對映到螢幕歸一化裝置座標的[-1,1]之間。歸一化螢幕座標是右手座標系統,原點在螢幕正中心,向右為x軸正方向,向上為y軸正方向,z軸垂直螢幕向外。以豎屏為例,比如設定left=-1,right=1,bottom=-hight/width,top=hight/width,比如我的手機解析度為1920*1080 =1.8 對上面的正方形點(0.5,0.5)座標而言經過變化就成了(0.5,0.3)
在螢幕的歸一化裝置座標中來看就是一個正方形了,因為y軸範圍顯然比x軸大,0.3對應的實際長度和x軸的0.5長度是一樣的。
上面的程式碼需要做如下修改,在onSurfaceChanged裡面增加如下程式碼
@Override
public void onSurfaceChanged(GL10 gl, int width, int height) {
GLES20.glViewport(0, 0, width, height);
// 根據螢幕方向設定投影矩陣
float ratio= width > height ? (float)width / height : (float)height / width;
if (width > height) {
// 橫屏
Matrix.orthoM(mProjectionMatrix, 0, -ratio, ratio, -1, 1, 0, 5);
} else {
Matrix.orthoM(mProjectionMatrix, 0, -1, 1, -ratio, ratio, 0, 5);
}
}接著在頂點著色器中對頂點乘以投影矩陣
private String vertexShaderCode = "uniform mat4 uProjectionMatrix;" // 增加這一行
+ "attribute vec3 aPosition;"
+ "void main(){"
+ "gl_Position = uProjectionMatrix * vec4(aPosition,1);" // 不是直接賦值而是乘以投影矩陣
+ "}";最後增加獲取著色器中uProjectionMatrix以及傳入值的程式碼部分即可。最終的效果不論橫屏還是豎屏,顯示的都是我們期望的正方形。
攝像機設定
需要補充的是,上面的引數near、far的含義指的是和視點的距離,視點貌似到目前還未接觸到,它指的是攝像機的位置,和實際生活中用相機看物體一樣,從不同的角度和位置拍攝同一個物體獲得的照片肯定是不一樣的,攝像機位置用setLookAtM函式指定。
public static void setLookAtM(float[] rm, // 生成的攝像機矩陣
int rmOffset,
float eyeX, float eyeY, float eyeZ, // 攝像機的位置
float centerX, float centerY, float centerZ, // 觀察目標點的位置
// 攝像機位置和觀察目標點的位置確定了觀察方向
float upX, float upY,float upZ // up向量在x、y、z軸上的分量,我覺得一般應該是和觀察方向垂直的
)前面提到的確定的視景體就和上面函式指定的攝像機位置和觀察方向有關。攝像機預設位置在(0,0,0)處,在上面的設定下,如果將改正方形沿z軸正方向平移1個單位,螢幕上就顯示不了,因為已經跑到了設定的視景體外面了。
關於攝像機的引數和投影near和far引數的設定需要注意,肯定不是胡亂設定的!攝像機的位置、方向和投影矩陣定義的視景體最終確定了視景體的位置,如果設定不當就會導致物體沒有顯示在螢幕上,因為物體的座標可能位於視景體外面。
視口
前面說過在視景體中的物體最終會投影到近平面上,最終顯示到視口上,正如前面在onSurfaceChanged設定的那樣。
public static native void glViewport(
int x,
int y,
int width,
int height
);視口中各引數的含義
視口用的螢幕座標系原點並不在螢幕左上角而是在左下角,x軸向右,y軸向上。其實還不是很準確,準確的說,視口的座標原點位於該View的左下角,因為GLSurfaceView並不總是佔據整個螢幕的。