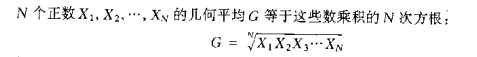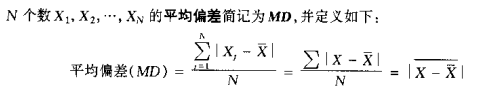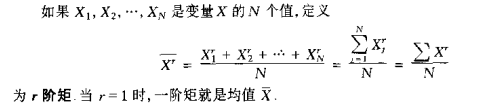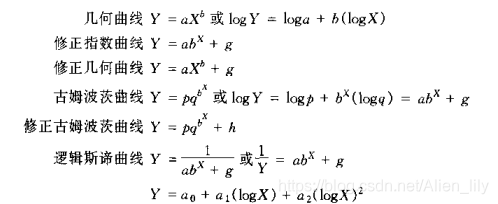1. 變數
   我們需要了解幾個名詞：
   變數、常量、連續變數、離散變數、連續資料、離散資料、自變數、因變數、函式、單值函式、多值函式
   以上名詞大家都比較理解，我這邊就解釋下什麼是單值函式和多值函式：
   單值函式：若對定義域每一個自變數x，其對應的函式值f(x)是唯一的，則稱f(x)是單值函式。
   多值函式：若│f(x)│=2x-1，則f(x)=±(2x-1)，一個自變數x對應兩個函式值。
2. 頻數分析
   陣列陣列：原始資料按照資料大小升序或降序排列，最大值與最小值的差為全距；
   組距、組限、組界、組中值、直方圖與頻率多邊形
   頻率分佈 = 某一組頻數/總頻數
   累計頻數分佈/累計頻數表，累計頻數多邊形/卵形線
   累計頻率分佈/百分率累計頻數 = 累計頻數/總頻數
3. 均值、中位數、眾數（集中趨勢的度量）
   平均值/集中趨勢的度量：趨向落在根據數值大小排列的資料的中心
   算數平均：
   
   N個數的算術平均簡稱均值
   加權算術平均：

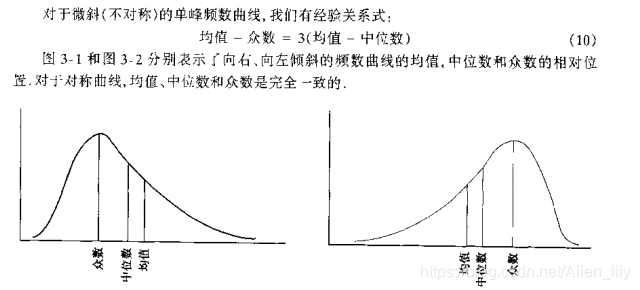
均值、中位數和眾數之間的關係：

幾何平均G：

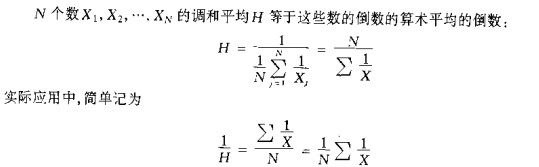
調和平均H：


均方根RMS

4. 標準差和其他表示利差的度量
   離差/變差：
   數值資料圍繞其平均值分佈的分數與集中程度，常用的有全距、平均偏差、半內四分位數間距，10-90百分位數間距、標準差；
   全距：最大值-最小值
   平均偏差
   
   半內四分位數間距：
   
   10-90百分位數間距：
   
   標準差：
   

方差：標準差的平方
離差度量間的關係：

5. 矩、偏度、峰度
矩：

r階中心矩：

（備註：關於矩這一個知識點，我其實還不能很明白的解釋清楚）
偏度：分佈不對稱成都或偏離對稱成都的反映

峰度：分佈的陡峭程度，尖峰、扁峰、常峰態
6. 初等概率論
概率：

條件概率，獨立和不獨立事件


互不相容事件：兩個或多個事件中，任意兩個事件都不能同時發生。

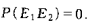
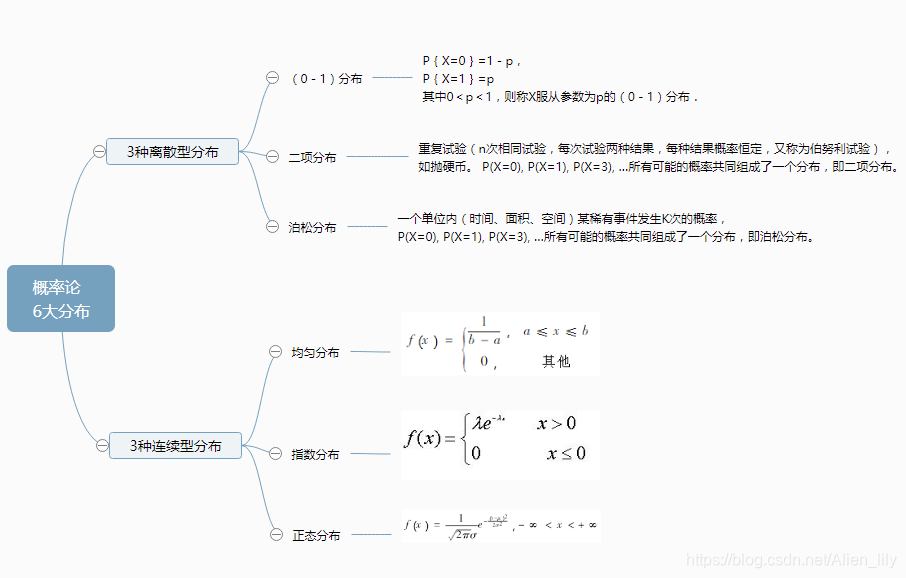
概率分佈：
離散型：離散型概率分佈
連續型：概率密度函式，連續型概率分佈
數學期望：在概率論和統計學中，數學期望(mean)（或均值，亦簡稱期望）是試驗中每次可能結果的概率乘以其結果的總和，是最基本的數學特徵之一。它反映隨機變數平均取值的大小。大數定律規定，隨著重複次數接近無窮大，數值的算術平均值幾乎肯定地收斂於期望值。
7. 二項分佈


正態分佈：


正態分佈與二項分佈的關係：

泊松分佈：

多項分佈：

8. 初等抽樣理論
隨機樣本、隨機數、有放回和無放回抽樣
抽樣分佈：
均值的抽樣分佈

標準誤差：
一個統計量的抽樣分佈的標準差常稱為該統計量的標準誤差

9. 統計估計理論
   無偏估計：如果一個統計量的抽樣分佈的均值等於相應的總體引數，那個這個統計量引數就是此引數的一個無偏估計量；否則，就稱為有偏估計量。統計量的相應值分別稱為無偏估計或有偏估計，估計量也常簡稱為估計。
   有效估計：如果兩個統計量的抽樣分佈有相同的均值（或期望），那麼方差較小的那個統計量稱為此均值的有效估計量，另一個稱為無效估計量。統計量的相應值稱為有效估計或無效估計。
   在均值的所有無偏估計量中，方差最小的那個統計量常被稱為此均值的最有效估計量或最優估計量。
   點估計和區間估計：如果一個數來估計總體的引數，那麼這種估計叫做引數的點估計。如果給出兩個數，指出引數位於其間，那麼這種估計叫做引數的區間估計。
   區間估計更加精確，因為要優於點估計。

10. 統計決策理論
    統計假設、零假設/原假設、備擇假設
    假設檢驗、顯著性檢驗/決策法則
    第一類和第二類錯誤：
    當我們拒絕了一個本應接受的假設時，我們就犯了第一類錯誤，反之，當我們接受了一個本應拒絕的假設時，我們就犯了第二類錯誤。無論是哪種情形，在判斷上我們都犯了錯誤，做出了錯誤的決策。
    正態分佈的檢驗，雙邊檢驗和單邊檢驗，特殊檢驗

11. 小樣本理論
    樣本容量N<30時，我們稱為小樣本，對小樣本統計量的抽樣分佈的研究稱之為小樣本理論，得到的結論不僅適用於小樣本問題，也適用於大樣本問題，也稱為精確抽樣理論。
    （注意：這邊的t分佈，卡方分佈，F分佈都沒有很清楚的解釋）

12. 曲線擬合和最小二乘法
    
    

概率論中的六種常用分佈，即（0－1）分佈、二項分佈、泊松分佈、均勻分佈、指數分佈和正態分佈。