因為最近看normL2face 看到中途發現作者其中有個創新點是對contrastive loss 和triple loss 進行了改動，由於之前只是草草的瞭解了contrastive loss ，為了更好地探究作者的創新出發點 ，看了contrastive loss 的論文 Dimensionality Reduction by Learning an Invariant Mapping
做一個簡單的總結.
在識別領域的損失,一般用於分類，但是此論文的損失在分類的基礎上有了附加的作用，用來降維。即本來相似的樣本，在經過降維（特徵提取）後，在特徵空間中，兩個樣本仍舊相似；而原本不相似的樣本，在經過降維後，在特徵空間中，兩個樣本仍舊不相似。同樣，該損失函式也可以很好的表達成對樣本的匹配程度。
問題

：降維涉及到將一組高維輸入的點對映到低維流形，以便將輸入空間中相似的點對映到流形的附近點。大多數現有的技術解決這兩個問題都有兩個缺點：1.大多數依賴於輸入空間的有意義的且可以計算距離度量的資料。2.沒有一個函式能夠精確對映輸入樣本的函式，而且這些樣本與訓練資料的關係也是未知的。
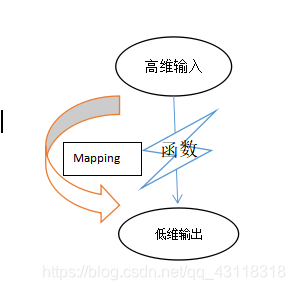
解決方法：論文提出一種用於降維的不變對映。通過學習一個全域性一致的非線性函式，將資料均勻的對映到輸出流形。學習完全依賴於鄰域關係，不需要在輸入空間測量任何距離。
總的來說，就是作者構造了一個函式，這個函式通過樣本對的比對，間接意義上實現了樣本降維，同時更新了權值，很好的表達了樣本的匹配程度。
傳統的降維方法：PCA： 將輸入投影到使方差最大化的低維子空間
MDS：計算出最能保持輸入點之間兩兩距離的投影
這個‘函式’的性質：1.在輸出空間的距離度量近似輸入空間中的領域關係（也就是說，輸入空間是相似的，輸出空間也是相似的）
2.對映不只是距離度量，還能夠學習複雜轉換的不變性（也就是說，在輸入向輸出對映，高維向低維對映的這個過程中，是由一定的規律的，相似點之間是有不變性的，這個規律是可以學到的）
3.這個對映應該是準確的，即便是未知領域關係的樣本。
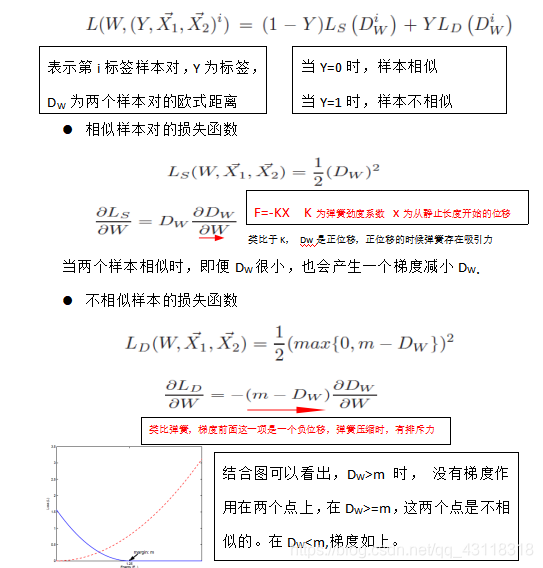
**理解：**作者用彈簧的拉伸位移與彈簧的吸引力和斥力，類比於對比損失函式 中的相似對與不相似對之間的損失函式大小。
以下是演算法理解：


接下來，會看相關程式碼 持續更新對比損失的實現。